1.2 Фізичні основи sps процесу

Типовий приклад імпульсного спікання – процес з використанням розряду в конденсаторній установці, схема якої показана на рис.5. У такому процесі струм, в ході розряду батареї проходить через порошок, засипаний в ізолюючу прес-форму. При цьому відбувається нагрівання і спікання частинок. Одночасно струм породжує інтенсивне магнітне поле. У результаті взаємодії магнітного поля з породжуючим його струмом виникають сили, які прагнуть обжати порошок в радіальному напрямку. Тому після такого розряду спечений зразок, як правило, вільно виймається з прес-форми. Слід однак, пам'ятати що помітна усадка внаслідок зазначеного обтиснення має місце лише в разі значень енергії в певному інтервалі. Цей енергетичний інтервал залежить від маси і природи матеріалу порошку, а також від розмірів зразка.

Рис.5. Схема установки для спікання електричним імпульсом: 1- конденсаторна батарея, 2 – розрядник, 3,6 – електроконтакти, 4 – матриця, 5 – порошок.

Струм при занадто високій енергії розряду спочатку призводить до плавлення стовпа порошку в його центрі по всій висоті. Занадто мала енергія розряду породжує недостатньо сильне магнітне поле, для того щоб відбулося обтиснення порошкового стовпа. Процес залежить від ряду параметрів електричного кола і характеристик порошку, які впливають в кінцевому рахунку конденсатора. На властивості одержуваного зразку. У загальному випадку при розряді через порошок можна виділити п'ять стадій:

1) руйнування поверхневих домішкових (наприклад, оксидних) шарів між суміжними частинками в осьовому напрямку при додатку критичної напруги, специфічного для даного порошкового матеріалу і конкретних геометричних розмірів завантаження; різко зростаючий струм йде по шляхах найменшого опору, опір завантаження майже миттєво падає;

2) міжчасткове спікання з утворенням паралельних напрямку протікання струму провідників у вигляді ''гірлянд" або ''ниток", між частинками утворюються всі великі шийки, це повинно супроводжуватися подальшим падінням опору, проте нагрів підвищує опір частинок в об'ємі; коли міжчасткове спікання перестає впливати на загальний опір, його зростання внаслідок нагрівання може виявитися переважаючим;

3) виникаюче внаслідок пінч-ефекту обтиснення ''ниток" і, як наслідок, подальше руйнування поверхневих домішкових шарів між частинками, контактуючими в радіальному напрямку, і наступне за ним посилене спікання в цьому напрямку;

4) проходження струму по суцільному утвореному шляху;

5) дезінтеграція, втрата стабільності або електровибух;

Розглянемо процес в трубчатій прес – формі, яка містить засипаний порошок і закритий з обох кінців контактуючими з порошком електродами рис.5 [10].

Як показали досліди [10], отримані зразки володіють невисокою щільністю (до 60%) проте їх міцність достатня для проведення наступної обробки, зокрема механічної.

Проаналізуємо закономірності процесу проходження струму послідовного ланцюга, який містить конденсаторну батарею ємністю С, індуктивність L і циліндричний порошковий зразок з опором R. Складність аналізу електроімпульсного спікання полягає в тому, що опір R змінюється в процесі спікання. Як показано в роботі [11] з часом спікання τ опір порошку R(τ), Ом, змінюється по закону:

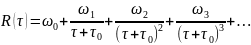(1)

де (n = 0,1,2…); – постійні параметри. Знайдемо вираз для напруги U(τ), В і струму І(τ), А, при початкових умовах:

U(0) = 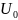; І(0) = 0. (2)

Напруга в ланцюгу установки – порошкова загрузка (еквівалентна схема показана на рис.6 ) підпорядковується диференційному рівнянню:

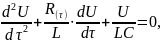(3)

де L – індуктивність, Г; С – ємність, Ф.

Спочатку розглянемо процес при умові:

(4)

коли опір порошкового зразка перевищує реактивний опір ланцюга.

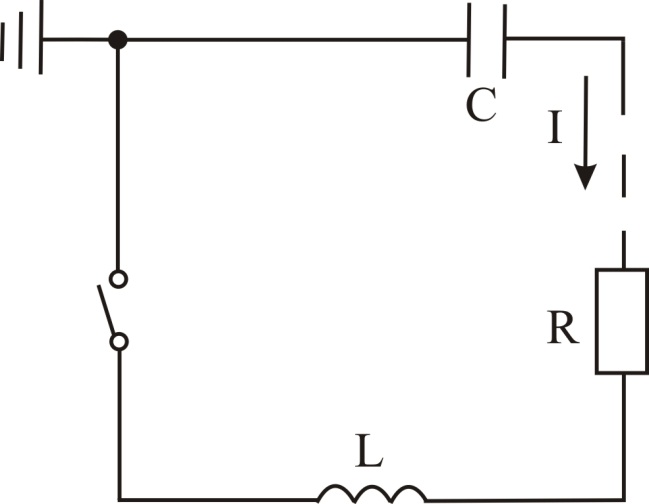
Рис.6. Еквівалентна електрична схема конденсаторної установки для спікання імпульсним струмом

При цьому треба взяти до уваги, що в залежності від відстані міжчасткових контактів прикладеною різницею потенціалів може призводити до різних результатів [12]. Через заготовки, чий питомий опір в напрямку проходження струму не менше 0,1 Ом·см, буде проходити струм недостатній для спікання. У випадку виконання умови (4), електричний розряд має аперіодичний характер. Напруга при врахуванні початкових умов (2) описується виразом:

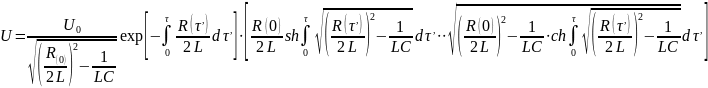(5)

де R(τ) задається формулою (1), опір порошку в початковий момент отримується із (1) при τ=0:

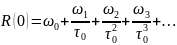(6)

Формула для струму отримується із співвідношення з використанням виразу (5):

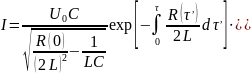(7)

Оскільки в рівнянні (4) коефіцієнт при 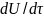залежить від часу, у виразах (5) і (6) під знаком гіперболічних тригонометричних функцій стоять не вирази які містять час τ, а інтеграли які виходять при розв’язанні радіального хвильового рівняння.

Вирази які входять у (5) і (7) можна обчислити використовуючи (1):

(8)

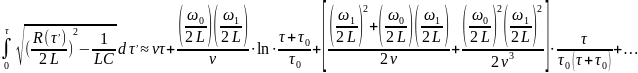
де ν – частота, яка визначається:

.

Перейдемо до процесу, протікаючому при виконанні нерівності, зворотного нерівності (5):

(9)

В цього випадку розряд має характер коливного процесу. Для напруги і струму отримаються наступні вирази:

(10)

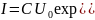(11)

де

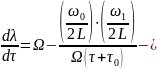
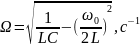
Формула для струму приймає вигляд:

,

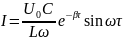де β – декремент затухання ; ω – кругова частота

Формули (7) і (11) справедливі для випадку коли R змінюється плавно в ході процесу, і не справедливі для випадкових змін R які можуть відбуватися наприклад внаслідок вибухоподібного руйнування оксидних плівок в результаті нагріву до високої температури.

Своєрідна ситуація виникає коли в ході розряду відбувається свого роду інверсія.

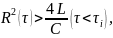
(12)

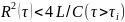
Такий процес повинен спочатку (0<τ<τ_i) розвиватися як аперіодичний, згідно розв’язку (7), а починаючи з моменту τ= τ_i як затухаючий періодичний, згідно розв’язку (11), в яке однак замість U₀ має бути підставлено U(τ_i) по формулі (7) і відлік часу має вестися від моменту τ_i (рис.7, а). Це різко відрізняється від того, що зазвичай відбувається в коливному контурі (рис.7, б).

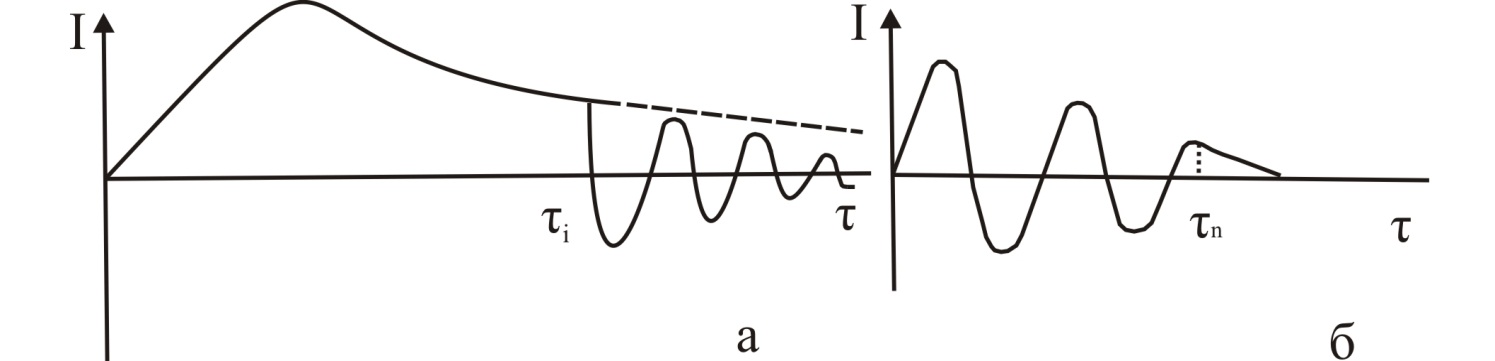
Рис.7. Часові залежності струму при розряді конденсатора через порошок з переходом від аперіодичного (τ<τ_i) розряду до затухаючого періодичного (τ>τ_i) розряду (а) і від затухаючого періодичного розряду (τ<τ_n) до аперіодичного (τ>τ_n) розряду (б). Штрихова лінія – функція струму якою описувався би процес при зберіганні аперіодичного характеру розряду.

Такого роду ефект можна очікувати не тільки при спіканні порошку, але і при використанні в контурі будь-якого зменшуваного з часом активного опору. Крім того, що порошкові частинки завдяки струму припікаються одна до іншої, порошок при пропущенні струму, як уже вказувалося, піддається обтисненню електромагнітними силами. Якщо струм рівномірно (з однаковою щільністю) розподілений по перетину циліндричного порошкового стовпа радіуса r₀, то тиск р(r), Па, в ньому може бути визначено за формулою:

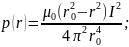(13)

де 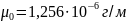(магнітна постійна); r – радіальна координата, м; І – сила струму, А.

Розподіл тиску (13) аналогічний розподілу тиску в провідному рідкому стовпі з струмом (схематичне зображення рис.8.а)

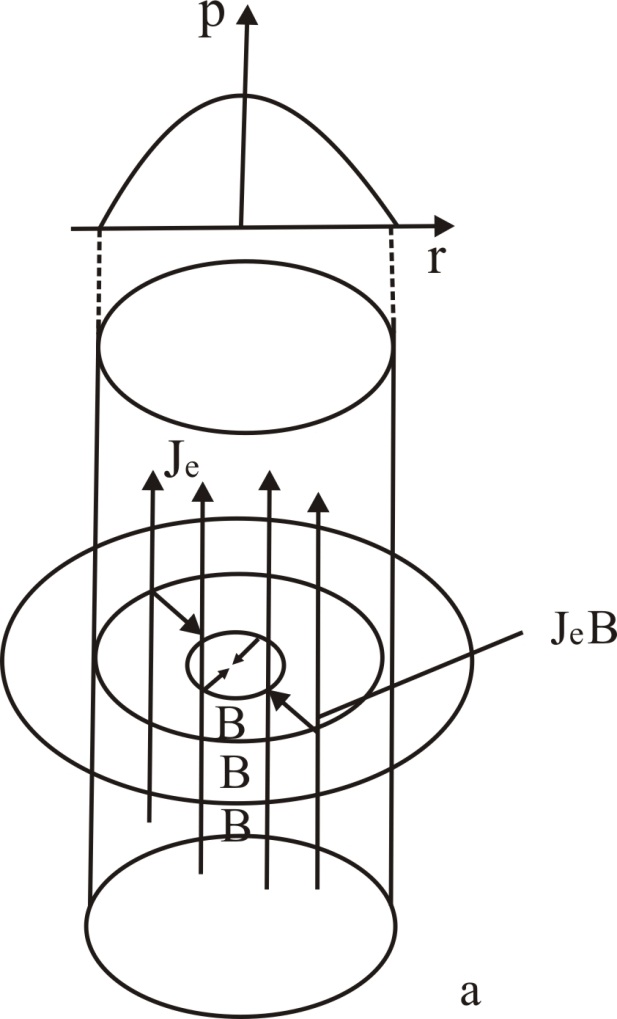
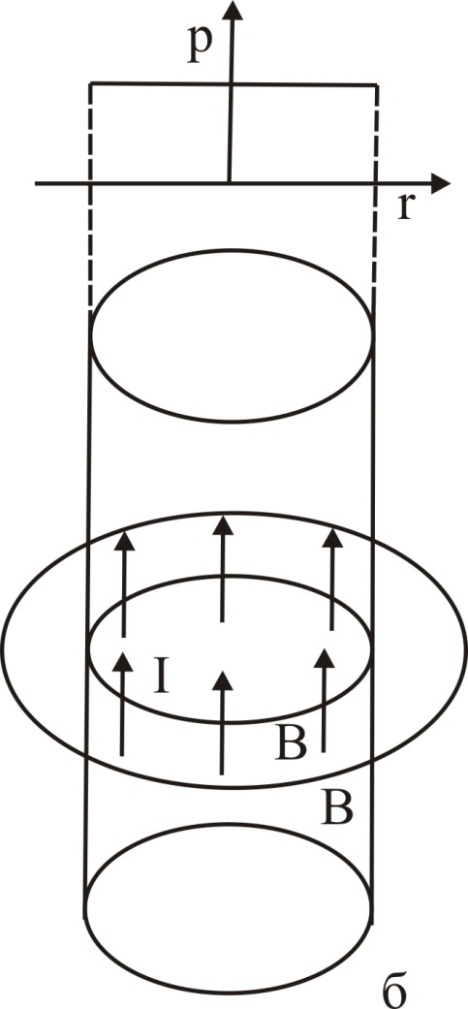
Рис.8. Пінч – ефект в порошку який спікається і епюри тиску p:

а – однорідний розподіл струму І в провідному стовпі порошку; б – провідник з поверхнісним струмом.

Для визначення тиску в ході розряду у формулу (13) необхідно підставити у випадку аперіодичного розряду вираз (7), у випадку періодичного вираз (11). Із формули (13) слідує що тиск на різних відстанях від осі пресування різний.

Опір порошку може бути визначено шляхом вимірювання різниці потенціалів на кінцях порошкового стовпа 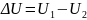, виходячи із виразу:

рівносильне рівнянню (4), отримаємо:

де, 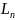– індуктивність порошкового стовпа, Г; 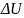– різниця потенціалів на кінцях пресованого матеріалу, В; I – струм який проходить через матеріал який пресується, А.

Для дослідження цілого ряду явищ які протікають при пресуванні матеріалу зв’язаних з особливостями нестаціонарного теплового режиму, необхідно знати просторове і тимчасове розподілення температури в матеріалі який пресується [13]. Розподіл температури в зразку визначається розподілом щільності струму в зразку з умовами тепловідводу. Розподіл щільності струму в зразку в свою чергу залежить від розподілу температури в ній. В зв’язку з цим необхідно спільно вирішувати теплову і електродинамічну задачу для зразка.

Розподіл щільності струму в зразку визначається рівнянням квазістаціонарного струмопереносу із врахуванням питомого опору від температури

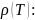
(14)

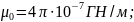ϳ - щільність струму в зразку. Розподіл температури в зразку визначається джоулевим нагрівом:

(15)

і умовами теплообміну зразка циліндричної форми (висотою 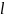і радіусом ) з не електропровідною матрицею на боковій поверхні

(16)

і умовами теплообміну на торцях прес – форми з електродами – пуансонами

(17)

де, Т – перевищення температури зразка над температурою матриці і пуансонів; γ – щільність; – теплоємність; χ – коефіцієнт теплопровідності пресуємого матеріалу; – коефіцієнти тепловіддачі з бокової і торцевої поверхонь прес – форми відповідно.

Вирішення сформованої задачі (14) – (17) в загальному випадку можливо з допомогою числових методів. Однак аналіз системи (14) – (17) дозволяє виявити основні критерії і параметри, які визначають характер теплового режиму пресування без точного вирішення задачі, а також сформулювати спрощену схему теплових режимів пресування. Така наближена схема відображає основні закономірності загальної задачі, і крім того допускає аналітичне вирішення задачі, що дає явну залежність розподілу температури від параметрів імпульсу струму і зразка.

Розглянемо пізніші стадії нагріву матеріалу який пресується з врахуванням їх охолодження за рахунок тепловідводу. В цьому випадку можна знехтувати залежністю питомого опору від температури ρ≈const. Тоді електродинамічна задача рішається окремо від теплової і у випадку циліндричної симетрії 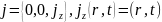визначається із рівняння (17) при умові, що

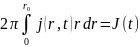(18)

– повний струм, який протікає через зразок; 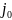– характерна щільність струму; 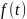– безрозмірна функція часу.

Нерівномірний розподіл щільності струму в зразку призводить до нерівномірного розігріву, нерівномірного припресування зразка і виникнення в зразку залишкових термонапруг. Вказані небажані явища визначаються відношенням між тривалістю теплових процесів в зразку і часом ущільнення матеріалу 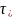під дією зовнішнього механічного тиску. Для всіх способів пресування (14) – (17) – час ущільнення, – час нагріву зразка імпульсом.

Розподіл температури в зразку визначається рівняннями (14) – (16), які при спрощеннях зводяться до наступного вигляду для безрозмірної температури де – температуропровідність матеріалу зразка.

(19)

(20)

(21)

де, 𝜑( ) – безрозмірна функція координати 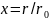, яка характеризує степінь розподілу струму по радіусу.

Розв’язок рівнянь (19) – (21) з врахуванням умови (18) тривіальним способом знаходиться методом поділу змінних. Із загального вигляду слідує закон охолодження зразка в залежності від умов тепловідводу.

(22)

де, 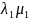– найменші корені трансцендентних рівнянь

(23)

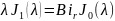(24)

Тут, 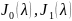– функції Бесселя нульового і першого порядку. Характерний час релаксації температури 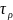шляхом тепловідводу в матрицю і пуансони визначається із (22)

(25)

Значення 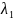і , отримані в результаті рівнянь (23), (24), в залежності від і 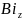наводяться на (рис. 9.) у вигляді графіків. Крива 1 відповідає розв’язку рівняння (23), крива 2 розв’язку рівняння (24).

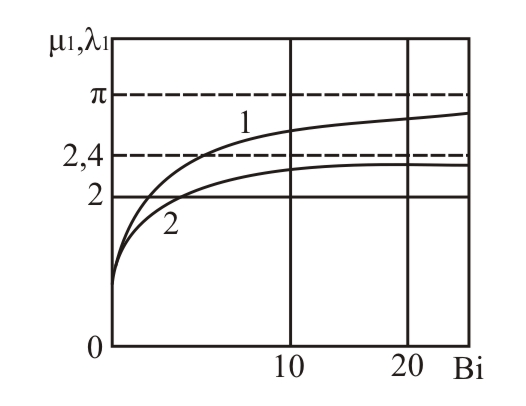
Рис.9. Залежність коренів рівняння (23), (24) від параметра Bi.

У випадку слабкого тепловідводу 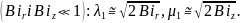При цьому зразок остигає значно повільніше, чим відбувається вирівнювання температури всередині зразка, і термонапруг в зразку не виникає.

Необхідно відмітити, що для найбільш ефективного режиму процесу пресування необхідно:

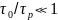
Для 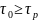відбувається непродуктивний нагрів пуансонів і матриці, а також більш швидке зношування пуансонів і матриці внаслідок високих температур, термонапруг, термоциклічних навантажень.

В залежності від відношення геометричних розмірів зразка можливі різні граничні умови охолодження зразка.

1. – довгий стрижень; , - тепловідвід в матрицю, при цьому значних термонапруг в стрижні не виникає, так як всередині стрижня температура вирівнюється швидше навіть граничного випадку 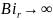і

2. – диск, – тепловідвід в пуансони, можливе виникнення значних термонапруг при так як .

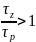Слід також відмітити істотне обмеження при електроімпульсному пресуванні і формуванні [14,15] зразків з відношенням , яке виходить із аналізу теплових процесів. В методах [14,15] використовується потужний високочастотний імпульс струму, і для рівномірного нагріву диска необхідно щоб скін – ефект не впливав на розподіл температури в зразку:

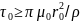
З другої сторони не повинно бути великого тепловідводу з поверхні диска:

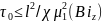
Обидва рівняння дають обмеження на :

(26)

Наприклад для порошку заліза із (26) маємо

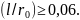
На процес ущільнення порошку впливає поряд з особливостями розподіл температури по об’єму всього зразка і неоднорідний разовий розігрів частинок порошкового середовища. При проходженні імпульсу струму через електропровідний порошковий матеріал найбільше енерговиділення відбувається на контактах між частинками порошку [15]. Поблизу контактів температура значно вища, ніж в об’ємі зерен порошку, і матеріал в області контактів значно деформується і може навіть плавитися [16].

Розглянемо умови виникнення рідкої фази на контактах між частинками порошку. Для імпульсів струму тривалістю тепловіддачею у внутрішнє середовище можна знехтувати, так як характерний час тепловіддачі 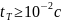[16]. При цьому введена в порошок енергія повністю іде на його розігрів. В залежності від параметрів імпульсу струму і характеристик порошкоподібного матеріалу можливі різні випадки прогріву частинок:

1. однорідний прогрів зерен порошку (температуропровідність речовини порошку);

2. неоднорідний прогрів зерен порошку .

Для однорідного прогріву частинок порошку момент виникнення рідкої фази в області контакту визначається із співвідношення:

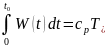(27)

Тут – потужність яка вводиться в порошок при проходженні імпульсу струму, Дж∙кг^-1∙см^-1; 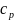– теплоємність речовини порошку, Дж∙кг^-1∙град^-1; - температура плавлення речовини порошку. Вираз (27) дозволяє легко оцінити момент виникнення рідкої фази в молібденовім порошку для імпульсів W₀=2,6∙10⁹ Дж∙кг^-1∙см^-1. (Така величина W₀ відповідає прямокутним імпульсам струму з макроскопічною щільністю струму в порошковім матеріалі )

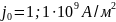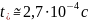(28)

При цьому 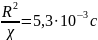– нагрів зерен порошку достатньо однорідний. Приведені вище оцінки показують, що для імпульсів струму з вказаною амплітудою і тривалістю плавлення в контактах частинок порошку не відбувається.

При неоднорідному прогріві зерен порошку 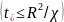геометрія контактних зон позначається на характері пресування. Розглянемо два можливих граничних випадки: – точковий характер контактів частинок порошку при малих тисках припресування (а – характерний розмір контактної зони) і 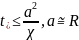– великий тиск припресування.

Для малих тисків припресування момент початку плавлення в контактах між частинками визначається відношенням:

(29)

де, – емпірична константа , характеризує середнє число контактів частинки порошку. При сталості введеної потужності із співвідношення (29) слідує результат: плавлення в контактах виникає з початку проходження імпульсу струму і триває до моменту часу обумовленого із (29):

(30)

Для великих тисків припресування утворення рідкої фази і контактної зони починається з часу яке визначається виразом:

(31)

Відношення (31) дозволяє також оцінити величину введеної потужності вище якої починає позначатися неоднорідність прогріву частинок порошку:

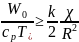(32)

(В оцінці (32) прийнято що )

Для порошку молібдену вираз (32) дає:

W₀=6,8∙10¹⁰ Дж∙кг^-1∙см^-1

Наведено оцінки, що дозволяють виявити вплив параметрів пресування і імпульсів струму на теплові процеси при електроімпульсному пресуванні.