13Б. Найти значение tg46о
14а. Студент знает ответы на 30 из 35 вопросов программы. Найти вероятность того, что он знает ответы на предложенные ему экзаменатором 3 вопроса.
14б. В июле 5 пасмурных дней. Какова вероятность, что 1-го и 2-го числа будет пасмурно?
15а. Задан закон распределения дискретной случайной величины Х. Найти:
а) математическое ожидание М(х); б) дисперсию D(х); в) среднее квадратическое отклонение (х).
Х 4 5 6 8
Р 0,3 0,4 0,2 0,1
15б. Х 6 7 8 10
Р 0,3 0,4 0,2 0,1
16А. Вероятность того, что цех своевременно выполнит заказ, равна 0,9. Найти вероятность того, что из 6 заказов будет своевременно выполнено не менее5.
16Б. Вероятность того, что цех своевременно выполнит заказ, равна 0,8. Найти вероятность того, что из 6 заказов будет своевременно выполнено 4 или 5.
17. Отдел технического контроля обнаружил 6 бракованных книг в партии из случайно отобранных 100 книг. Найти относительную частоту появления бракованных книг.
18. В урне 2 белых, 3 красных и 5 синих одинаковых по размеру шаров. Какова вероятность, что шар, наугад вынутый из урны (без возращения), будет цветным?
19а. Сколькими способами можно выбрать трех дежурных из группы в 20 человек?
19б. Сколькими способами можно расставить 5 книг?
21. Вычислить по определению производные след. Функций: x2, sin X, сos X
22.
Найти обратную матрицу
А=
В=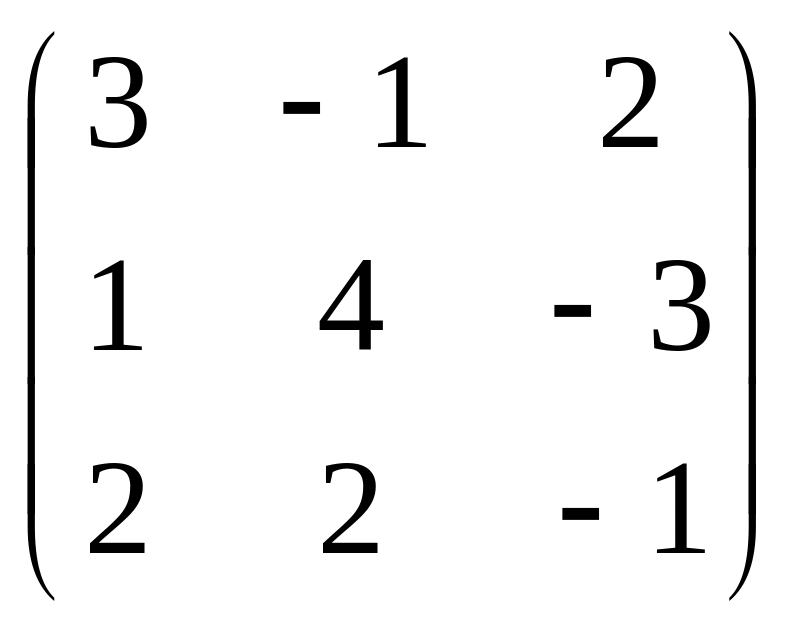
23. Построить выпуклый многоугольник, заданный системой неравенств и, пользуясь графическим методом, найти минимум и максимум линейной формы L = 2x1 + x2 + 3.
23.1.
23.2.
24. Дана вероятность р появления события а в каждом из п независимых испытаний. Найти вероятность того, что в этих испытаниях событие а появится не менее раз и не более раз.
п = 360, р = 0,8, = 300, = 320.
25. Известны математическое ожидание a и среднеквадратическое отклонение нормально распределенной случайной величины X. Написать плотность вероятности и найти вероятность попадания этой величины в заданный интервал (; ).
a = 11, = 5, = 5, =
Дальность полета
7 Легких
10 Средних
16 Трудных