1. Предмет теории вероятностей. Виды событий. Примеры. Испытания и события. Классическое определение вероятности. Свойства вероятности. Относительная частота.

2. Формулы комбинаторики: перестановки, размещения, сочетания. Примеры.

3. Сумма событий. Произведение событий. Примеры.

4. Совместные и несовместные, зависимые и независимые события. Примеры.

5. Теоремы сложения вероятностей совместных и несовместных событий.

6. Полная группа событий. Противоположные события. Примеры.

7. Теоремы умножения вероятностей зависимых и независимых событий. Условная вероятность.

8. Формула полной вероятности.

9. Повторные испытания. Формула Бернулли. Пример.

10. Повторные испытания. Интегральная ф-ла Лапласа (теоремы Лапласа).

11. Случайная величина. Дискретная и непрерывная случайные величины. Примеры.

12. Закон распределения дискретной случайной величины. Мат. ожидание, дисперсия и среднее квадратическое отклонение дискретной случайной величины.

13. Функция распределения вероятностей непрерывной случайной величины и её график. Вероятность попадания в заданный интервал. Пример.

14. Плотность распределения вероятностей непрерывной случайной величины и её график. Вероятность попадания сл. вел. в заданный интервал. Пример.

15. Числовые характеристики: мат. Ожидание, дисперсия и среднее квадратическое отклонение непрерывной случайной величины. Пример.

16. Нормальное распределение случайной величины. График нормального распределения. Вероятность попадания в заданный интервал нормальной случайной величины. Пример.

17. Математическая статистика. Генеральная и выборочная совокупность.

18. Статистическое распределение выборки. Вариационный ряд. Частоты, относительные частоты.

19. Графики статистического распределения: полигоны и гистограммы

47. . Что называется общим решением и частным решением дифференциального уравнения первого порядка (пример)? Что такое «задача Коши»? Для чего нужны начальные условия? Как выглядят графически общее решение, частное решение и начальное условие (для дифференциального уравнения первого порядка)?

48. Дифференциальные уравнения с разделяющимися переменными и их решение (пример).

49. Линейные дифференциальные уравнения первого порядка и их решение (пример).

Требования к ответу на экзамене.

Требования: ответ на теоретический вопрос должен содержать примеры, которые иллюстрируют теоретические положения и показывают, как применяется теория.

Решение примера (задачи) должно быть правильным, полным, мотивированным (содержать комментарии, в т.ч. обоснование применения используемых формул) и разборчиво написанным. Ответ без решения не засчитывается.

Критерии формирования экзаменационной оценки:

Отлично - студент не только знает теоретический курс, но и может применять его разделы на практике, умеет решать задачи и может обосновать решение.

Хорошо – студент недостаточно усвоил теоретический курс, но хорошо решает задачи и может обосновать решение.

Удовлетворительно – студент недостаточно хорошо усвоил теоретический и практический курс.

Неудовлетворительно – студент не усвоил теоретический и практический курс математики, в т.ч.не показал навыков решения задач.

Типовые задачи

Задание 1.

а. Начертить прямую y = –2х+4. Проходит ли она через точку (2; 5)?

б. Начертить прямую y = 3х/4 + 3. Проходит ли она через точку (4; 6)?

в. Написать уравнение прямой с угловым коэффициентом, проходящей через точки (1;2) и (–3;0).

г. Дана прямая y = –2х+4. Написать уравнение прямой, которая параллельна данной и проходит через начало координат.

д. Начертить линию _y=(1-x²₎^0,5

Задание 2. Даны матрицы А и В.

2.1. Найти С=2А+3В А= ; В= .

2.2. Найти С=3А-2В А=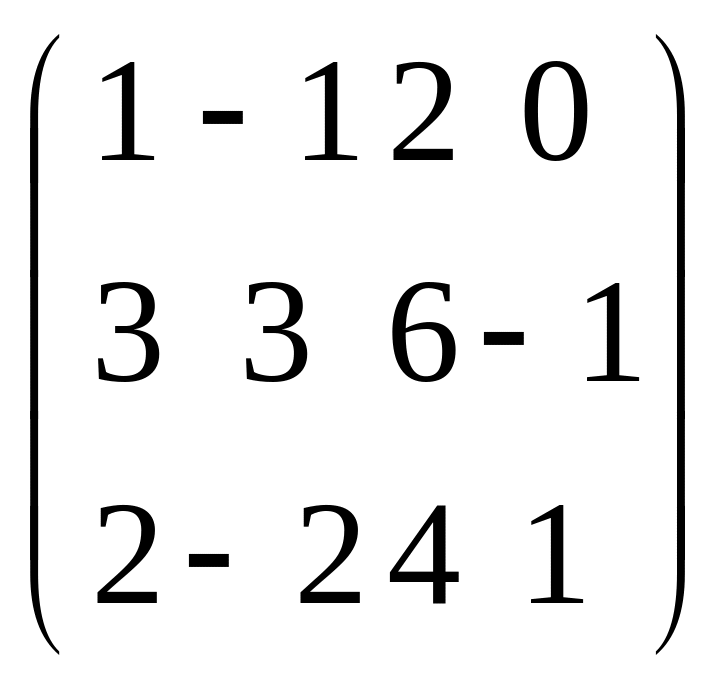 ; В= .

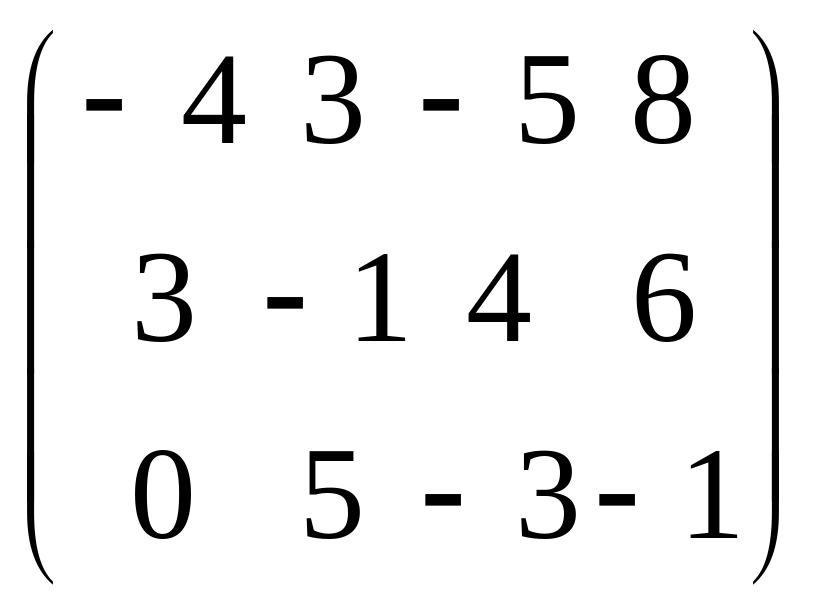Задание 3. Найти произведение АВ и ВА.

3.1 А= , В= . 3.2 А= , В= .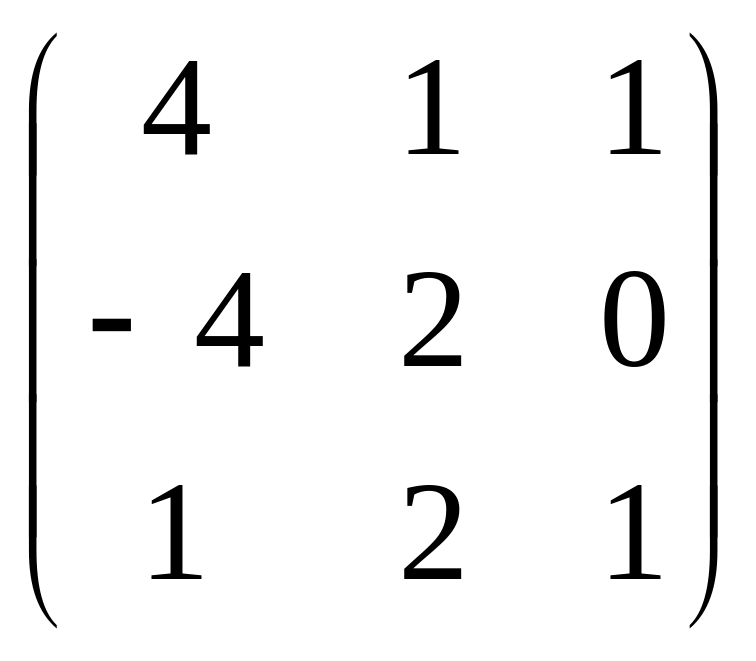

Задание 4. Привести матрицы к ступенчатому виду.

А= В=

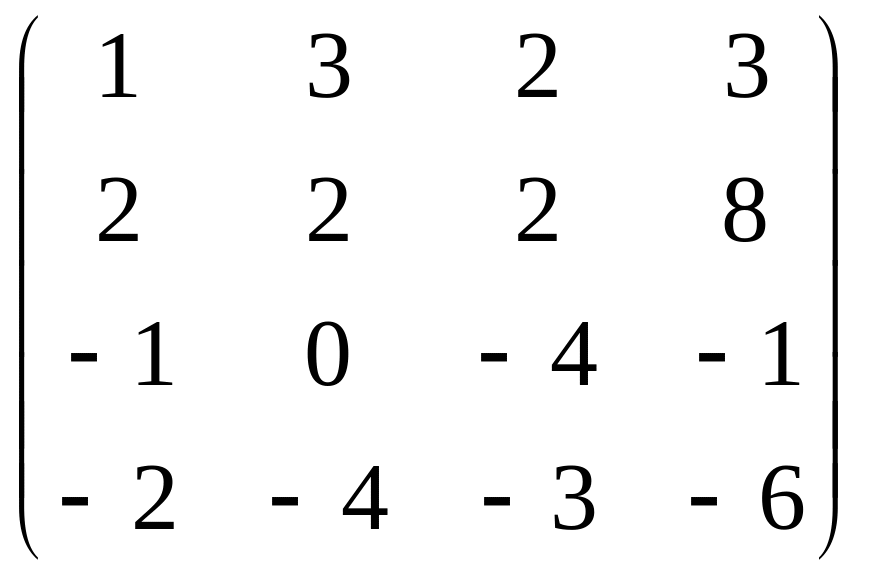
Задание 5. Вычислить определитель матриц.

А= В=

Задание 6. Решить систему линейных уравнений методом Крамера

6.1. 6.2.

Задание 7 Решить систему линейных уравнений методом Гаусса.

Те же, что в п.12.

Задание 1. Найти область определения функции.

а. ; б. .

Задание 2. Построить график функции, (перечислив шаги преобразования) и описать ее основные свойства: область определения, интервалы монотонности, четность – нечетность, точки разрыва.

Задание 3. Найти предел числовой последовательности и предел функции.

Задание 4. Определить координаты (х и y) точки, в которой касательная к графику функции – параболы - имеет наклон 45º к оси абсцисс. Начертить график функции и касательную. Выражение для функции y = x² - x +12, y = x² – 4x – 5

Задание 5. Дана функция y = x² - x +12. В какой точке касательная горизонтальна?

Дана функция y = x² -4 x -5. В какой точке касательная горизонтальна?

Задание 6.

6а. Вычислить наклон касательной в точке х=2 графика функции y = х² –2х+2

6б. В какой точке касательная к графику функции горизонтальна? y = х³ –2х+2

Задание 7. Найти производную функции.

а) y = б )

Задание 8. Зная производные основных элементарных функций и правила дифференцирования, вычислить производные след. функций :

а ) б )

Задание 9. Исследовать функцию и построить график.

у = ( х³ + 9х² + 15х – 9). у = х + 9/х

Задание 10. Найти неопределенный интеграл а)

б)

в)

Задание 11а. Найти с помощью определённого интеграла площадь плоской фигуры, расположенной в первом квадранте и ограниченной параболой прямой и осью OX.

11б. параболой y = 4x² прямой y = -2x+2 и осью OX.

Задание 12а. Найти с помощью определённого интеграла объём тела, образованного вращением вокруг оси ОХ фигуры, расположенной в первом квадранте и ограниченной параболой прямой х=2 и осью ОХ

Задание 12б. Найти с помощью определённого интеграла объём тела, образованного вращением вокруг оси ОХ фигуры, расположенной в первом квадранте и ограниченной прямой .

Задание 13а. Найти значение (4,008)^0,5