Действительные числа: рациональные, иррациональные. Дробные числа. Примеры.

Абсолютная величина (модуль) действительного числа. Свойства абсолютных величин. Построить график функции

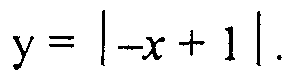
Понятие функции. Способы задания функции. Область определения и область значений функции на примере

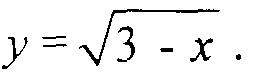
Функции четные и нечетные, периодические, монотонные, ограниченные и неограниченные. Примеры.

Элементарные функции. Основные элементарные функции и их графики.

Числовая последовательность. Общий член последовательности. Примеры. Монотонно возрастающая и монотонно убывающая последовательность. Примеры.

Предел последовательности. Сходящаяся и расходящаяся последовательность. Примеры.

Предел функции. Основные теоремы о пределах. Примеры.

Бесконечно большие и бесконечно малые величины. Их свойства и действия над ними. Примеры.

Раскрытие неопределенностей вида 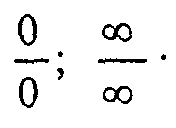Примеры.

Первый и второй замечательные пределы. Примеры:

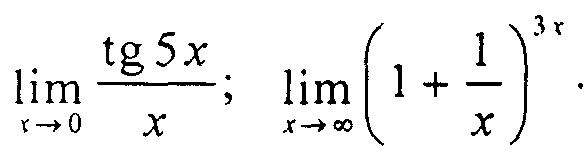
Приращение аргумента. Приращение функции. Пример.

Определение непрерывности функции. Доказать, что функция у = х² непрерывна для любого значения х.

Задача о скорости движения точки.

Задача о касательной. Уравнение касательной.

Определение производной. Ее геометрический и физический смысл.

Правила дифференцирования функции. Производная сложной функции. Примеры.

Доказать:

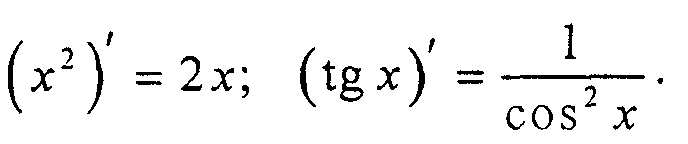
Таблица производных. Доказать справедливость двух формул.

Дифференциал функции. Его геометрический смысл.

Применение дифференциала для приближ. вычислений

Правило Лопиталя. Примеры:

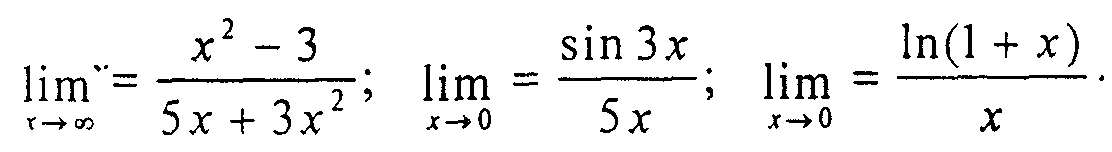
Возрастание и убывание функции. Найти интервалы возрастания и убывания функции

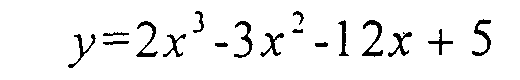
Необходимые и достаточные условия существования экстремума функции. Найти экстремумы функции

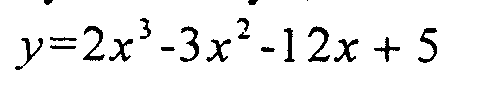
Выпуклость и вогнутость графика функции. Точки перегиба.

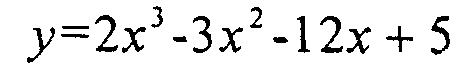
Наибольшее и наименьшее значение функции на данном отрезке. Пример: функция 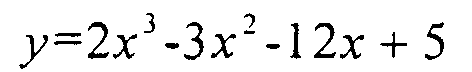отрезок [ -2;З].

Асимптоты. Вертикальные асимптоты. Наклонные и горизонтальные асимптоты. Пример:

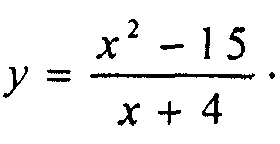
Общая схема исследования функции и построение графика.

Первообразная и неопределённый интеграл (определения).

Основные свойства неопределённого интеграла.

Таблица интегралов (12 -14 формул).

Основные методы интегрирования (перечислить. 3 примера.

Что такое определённый интеграл? Его геометрический смысл.

Основные свойства определённого интеграла.

Вычисление определённого интеграла по формуле Ньютона – Лейбница). Пример.

Вычисление площадей с помощью определённого интеграла (привести пример).

Вычисление объёмов тел вращения с помощью определённого интеграла (пример).

Непрерывность функции на интервале. Что означают слова: функция непрерывна слева, функция непрерывна справа. Точки разрыва функции.

Свойство функции непрерывной на отрезке (теорема).

Методы интегрирования по частям и замены переменной для определённого интеграла.

Интегрирование чётных и нечётных функций на отрезке, симметричном относительно начала координат.

Обратная функция и ее график. Примеры. Производная обратной функции. Найти производную функции у = arcsin х

Производная обратной функции. Найти производную функции у = arcsin х

Сложная функция. Примеры. Производная сложной функции

. Что называется общим решением и частным решением дифференциального уравнения первого порядка (пример)? Что такое «задача Коши»? Для чего нужны начальные условия? Как выглядят графически общее решение, частное решение и начальное условие (для дифференциального уравнения первого порядка)?

Дифференциальные уравнения с разделяющимися переменными и их решение (пример).