11. Основные метрологические понятия. Предел абсолютной допускаемой погрешности. Влияющие физические величины. Основная и дополнительная погрешности.

Предел абсолютной допускаемой погрешности средства измерения - это наибольшая (по модулю) абсолютная погрешность средства измерения, при которой он может быть признан годным ц допущен к применению. Эту величину для краткости часто называют предельной погрешностью.

Влияющая физическая величина - это величина, не измеряемая данным прибором, но оказывающая влияние на результат измерения.

Основная погрешность средства измерений - это предел абсолютной допускаемой погрешности средства измерений, используемого в нормальных условиях.

Дополнительная погрешность - это увеличение предельной погреш­ности средства измерения при отклонении одной из влияющих величин за пределы нормальной области (но при условии, что влияющая величина не выйдет за пределы рабочей области).

12. Основные метрологические понятия. Случайная и систематическая погрешности. Поправка.

Систематическая погрешность средства измерения - составляю- щая погрешности, остающаяся постоянной или закономерно изменяющаяся.

Систематическую погрешность нужно определять не по абсолютной величине, а с учетом знака. Это очень важно для введения поправки в пока­зания прибора.

Систематическая погрешность, не зависящая от значений измеряемой величины, называется аддитивной погрешностью.

Поправка - значение величины, одноименной с измеряемой, прибавляе­мое к полученному при измерении значению с целью исключения системати­ческой погрешности.

Случайная погрешность средства измерений - составляющая погреш­ности, остающаяся постоянной или закономерно изменяющаяся.

13. Понятие о классе точности. Четыре способа выражения классов точности.

Класс точности средства измерений - это обобщенная характери­стика средства измерений, определяемая пределами допускаемых основной и дополнительной погрешностей, а также другими свойствами средства измерений, влияющими на точность, значения которых устанавливаются в стандартах.

1. Класс точности задан числом ∆осн=(к*Д)/100

2. Класс точности задан 2 кружке ∆осн=(к*Х)/100

3. Класс точности задан с/d в этом случае ∆осн=х/100 *(с+d(|B/х|-1))

Где х-текущее показание прибора

В- верхний предел измерения

4. Класс точности задан римскими цифрами или буквами латинского алфавита. К буквам допускается присоединять индексы в виде арабских цифр в этом случае ∆п задается в виде графиков, таблиц сложных функций. Недостатком является условный характер.

15. Погрешности косвенных измерений и их определение.

Пусть у- величина подвергаемая косвенному измерению и у- есть функция у=f(x_1,x₂,…x_n), величины x_1,x₂,…x_n

Подвергаются прямым измерениям и каждое из них имеет предельную погрешность ∆x_1,∆x₂,…∆x_n, тогда абсолютная погрешность косвенного измерения: ∆у=|

Для функции вида:

1. у=х1+х2 ∆у=|∆x₁|+|∆x₂|

2. y=x1*x2 ∆у=|x₁|_*∆x₂+_*|x₂|*∆x₁

3. y= ∆у=

16. Элементы теории случайных погрешностей. Показание прибора как случайная величина. Функция плотности вероятности. Доверительный интервал и доверительная вероятность.

Случайные ошибки представляют не что иное, как случайные события по теории вероятностей. Гаусс, рассматривая случайные события, установил нормальный закон распределения случайной величины, который применим и для результатов измерений при наличии случайных ошибок Δx_i:

__ (-Δx²_i/2σ²)

f(Δx_i) = (1/ σ² √2π ) e (3)

г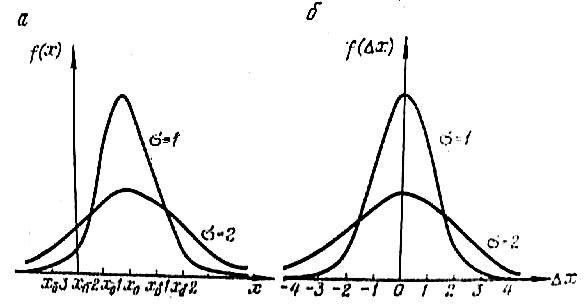 де f (Δx_i) – вероятность отклонения случайной величины x от ее наиболее вероятного значения x₀. Параметр σ в формуле (3) называется стандартной ошибкой, а ее квадрат σ² – дисперсией измерений. График функции f(Δx_i) для разных значений σ представлен на рис. 1, а, б.

Рис. 1.

Нормальная кривая разделяется на три зоны, каждой из которых соответствует определенная вероятность попадания случайной величины. В интервал от x_ср – s до x_ср + s попадает 68% всех измерений. В интервале от x_ср– 2s до x_ср+ 2s то есть с удвоенной стандартной ошибкой, укладывается 95% всех измерений, а в интервал от x_ср – 3s до x_ср +3s – 99,7%. Только 0,003% всех измерений выходит за пределы интервала (x_ср – 3s, x_ср +3s). Практически вероятность таких измерений равна нулю. Таким образом, удобство применения стандартной ошибки в качестве основного выражения погрешности измерения заключается в том, что ей соответствует математически обоснованная определенная вероятность, называемая доверительной вероятностью, а соответствующий ей интервал называется доверительным интервалом.