Метод припасовывания.

Идея метода в следующем – переходный процесс НЛС разбивается на участки соответствующие различным диапазонам регулируемой величины. Причем на каждом из пределов этих участков система может рассматриваться как НЛ-ая. Затем участки стыкуются друг с другом, конечное значение которого является начальным условием для другого.

Особенно этот метод эффективен для релейных систем, для которых он является точным.

Линейная часть

Нелинейная часть

Рассмотрим отрезок :

НЛ часть равна (7)+(5)

(8)+(5)

предположим, что известны начальные условия.

Дифференцируем уравнение (5):

:

(9)

:

,

(10)

с – свободное состояние

kc – вынужденное состояние

;

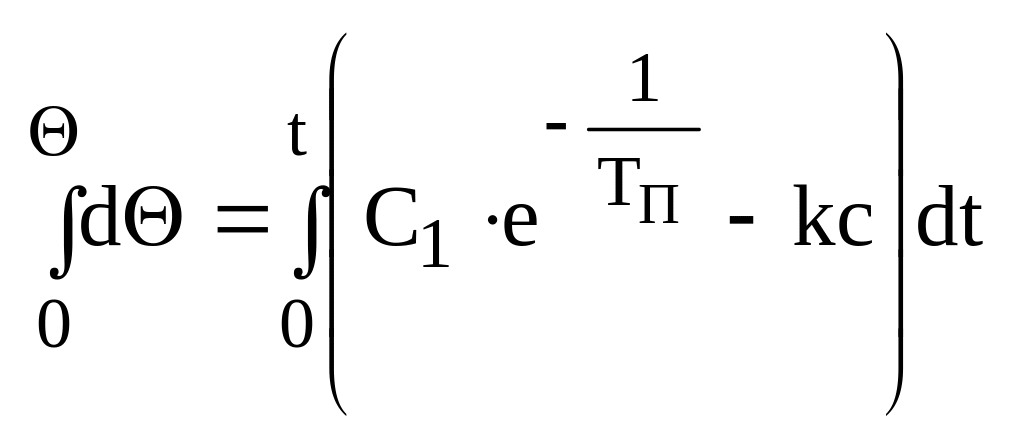
(11)

Уравнение (11) описывает изменение температуры во времени на участке АВ. Чтобы определить численные значения С₁ и С₂ перенесем в начало отсчета т. А,

тогда

- считаем известным

из уравнения (10): (12)

из уравнения (11): (13)

Решение на участке АВ полностью определено.

Поведение системы на участке описывается уравнением (5) и (8)

(14)

(15)

Уравнение (15) описывает изменение температуры на . Мысленно переносим начало координат в точку В.

Для этого можно воспользоваться уравнением (10), в котором С₁ определена из уравнения (12) в предположении, что .

Получим начальные условия для второго участка. Определяем имеются ли в системе автоколебания. Для этого:

1. выясним, есть ли в системе периодические движения (необходимое условие автоколебаний)

2. если в системе существуют периодические движения, определяем, устойчивы ли колебания. Если они устойчивы, то системе присущ автоколебательный режим.

1). Есть ли в системе периодические движения (они имеют место, если состояние системы в точке D повторяет состояние системы в точке А)

(16)

Если условие (16) выполняется, то в системе имеют место периодические движения.

Допустим, что (16) выполняется. Найдем период колебаний – вещественное положительное число, и на этом основании сделаем вывод, что периодические движения в системе возможны. Если в системе движения периодические, то период колебаний составлен двумя полупериодами.

(17)

Условие 1 в рассматриваемой системе выполняется автоматически, так как это фазопереключающая система.

Из (10) найдем и в соответствии с (17) запишем следующее:

Из (10) (18)

Из (12) подставим в (13)

(19)

для нахождения t₀ в уравнении (19)

С₁ найдем из (11) путем подстановки вместо получим

для определения С₂ используем уравнение (13)

(20)

поделим (20) на (19):

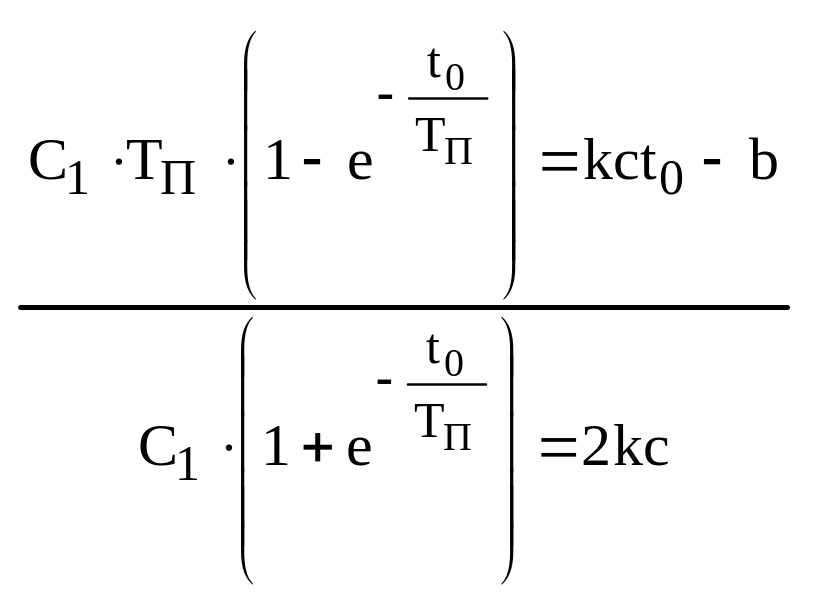
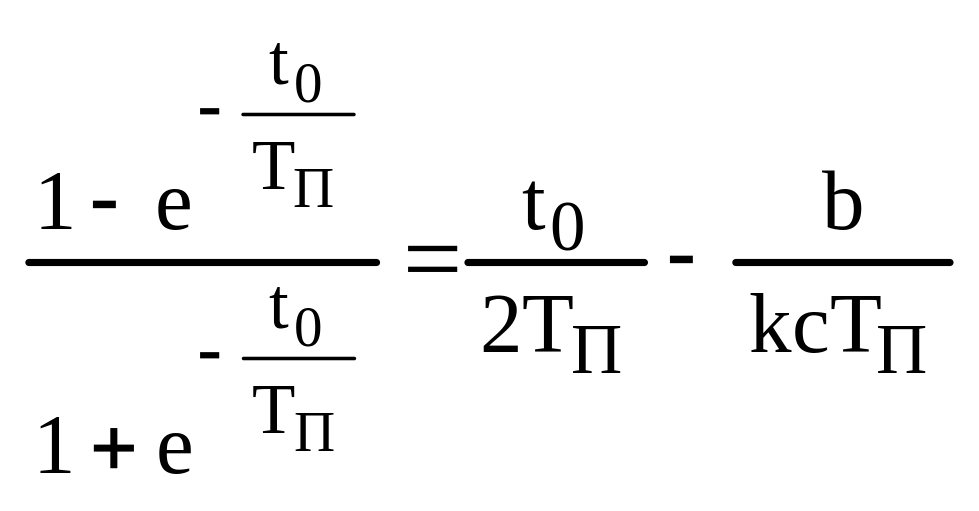
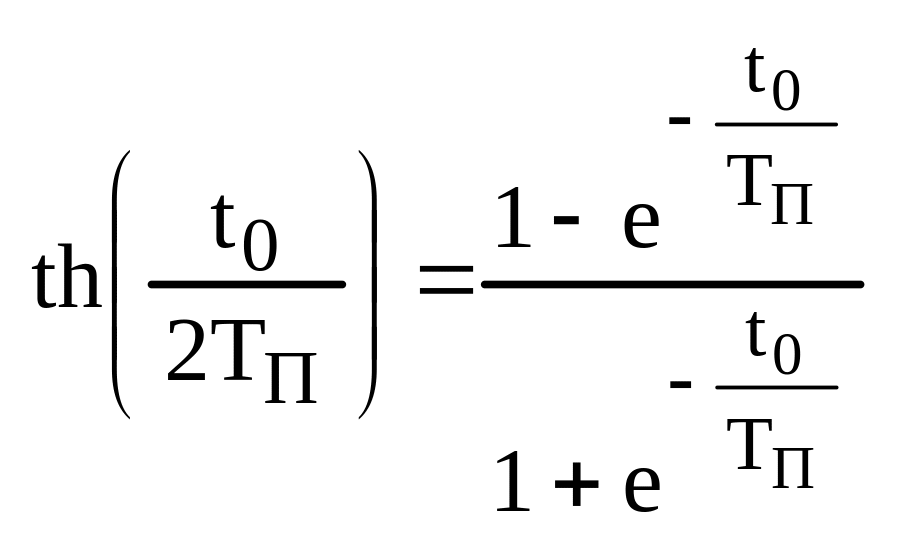
th – тангенс гиперболический.

- это уравнение трансцендентное решается графическим способом, так как аналитически оно не решается.

Нашли t₀ – положительное вещественное число. Значит, в данной системе могут быть периодические колебания. Чем больше b, тем больше t₀, то есть при больших значениях времени будут происходить переключения. Чем меньше с, тем больше t₀. Точно так же t₀ зависит от коэффициента k (обратно пропорционально). Влияние величины T_П иное, так как Т_П входит и в y₁ и в y₂, но обычно при увеличении Т_П увеличивается t₀. Если в (10) подставить численное значение C₁ и C₂, полученные из начальных условий по уравнениям (12) и (13), то, исследовав затем полученную функцию на экстремум найдем значение амплитуды колебаний.

По методу припасовывания находим период колебаний и амплитуду. Однако вопрос устойчивости не может быть решен в рамках этого метода. Необходимы другие методы.