- •Звено с многозначными характеристиками.
- •Статика нелинейных систем.
- •Преобразование нелинейных структурных схем.
- •Методика составления уравнения нлс.
- •Место для схемы печи!!!
- •Метод припасовывания.
- •Исследование устойчивости нлс на фазовой плоскости.
- •Формулировка теоремы Ляпунова об устойчивости систем.
- •Корни вещественные, отрицательные.
- •Корни положительные вещественные.
- •Корни вещественные различных знаков.
- •Особые точки и особые линии.
- •Случай соответствует системе на границе устойчивости.
- •Приближенные методы построения фазовых траекторий.
- •Метод гармонической линеаризации. (Метод гармонического баланса).
- •Устойчивость нелинейных систем.
Нелинейные системы.
Общая характеристика нелинейности.
Сложность – нет общего метода решения нелинейных дифференциальных уравнений.
Аппроксимация нелинейных систем до линейных.
Представление нелинейных элементов линейными.
линейные системы работоспособны только в том случае, когда они устойчивы, а нелинейные системы имеют неустойчивые режимы (автоколебания) даже в нормальных условиях работы.
для нелинейных систем неприменим принцип суперпозиции.
Нелинейные звенья систем управления.
![]()
Нелинейность можно классифицировать по различным показателям:
симметричность;
гладкость;
однозначность.
Симметрия: 1.
![]()

![]()
2.
![]()

![]()
Если функция не обладает свойствами 1 и 2, то несимметричная нелинейность.
Гладкость. Если
в любой точке
![]() существует
существует
![]() ,
то такая зависимость
называется гладкой.
,
то такая зависимость
называется гладкой.

Однозначность. Если для каждого значения х имеется определенное число z, то такая характеристика однозначна.
Нелинейная характеристика с определенным участком двузначности.
Многозначная нелинейная система.
Типовые нелинейные звенья.
Это звенья с однозначными непрерывными характеристиками.
1). «Зона нечувствительности».

![]()
Механическая модель звена типа «зона нечувствительности».

2). «Ограничение или насыщение».
Негладкая, так как
производная имеет 2 точки разрыва.
![]()
Механическая модель звена типа «ограничение или насыщение».

3). «Ограничение с зоной нечувствительности».

![]()
Механическая модель звена типа «ограничение с зоной нечувствительности».

Звенья с однозначными разрывными характеристиками.
1). Звено типа «двухпозиционное реле без гистерезиса».

![]()

2). Звено типа «трехпозиционное реле без гистерезиса».

![]()

при
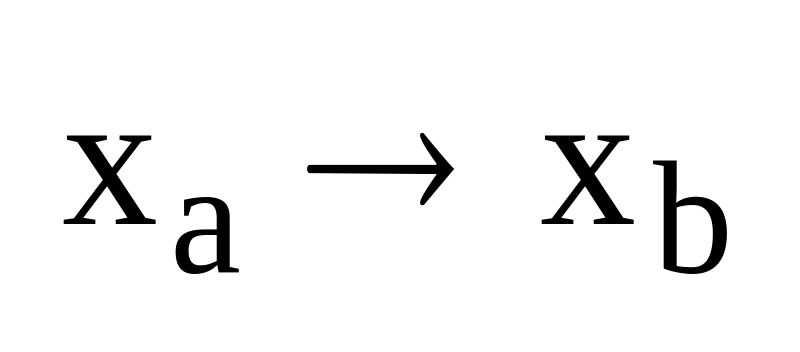 б)
при
б)
при
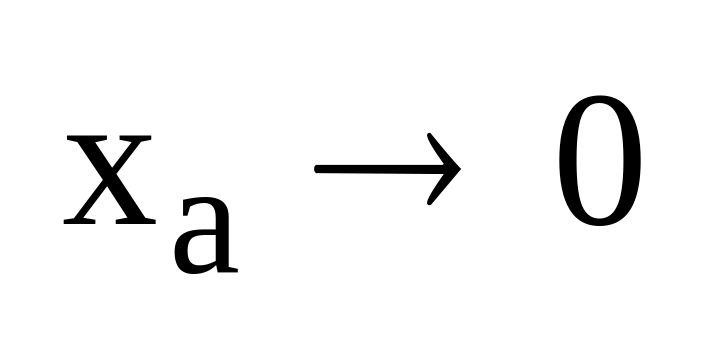 ,
,
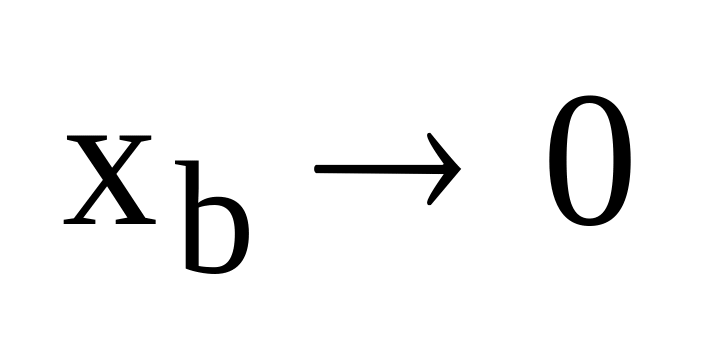

При анализе и синтезе нелинейных систем часто пользуются идеализированными характеристиками, полученными в результате предельных переходов.
Звенья с двузначными характеристиками.
Звено типа «двухпозиционное реле с гистерезисом».

![]()
На участке
![]() выходная величина z
имеет два значения zb
и
zb
в зависимости
от предшествующих значений х.
Эту зону двузначности ограничивают
переходы:
выходная величина z
имеет два значения zb
и
zb
в зависимости
от предшествующих значений х.
Эту зону двузначности ограничивают
переходы:
снизу вверх при
![]() и
и
![]()
сверху вниз при
![]() и
и
![]()
Звено типа «трехпозиционное реле с гистерезисом».

![]()
Переход от z=0
к
![]() происходит в точке
происходит в точке![]() ,
а обратный переход от
к z=0
происходит в точке
.
Зону двузначности на участке, где
,
а обратный переход от
к z=0
происходит в точке
.
Зону двузначности на участке, где
![]() проходим в соответствии со знаком
проходим в соответствии со знаком
![]() .
.
Звено с многозначными характеристиками.
З
 вено
типа «люфт».
вено
типа «люфт».

Если в нелинейности типа «зона нечувствительности» убрать механическую пружину, стремящуюся вернуть вал в нулевое положение, получим нелинейность типа «люфт».
Зависимость между
положением ведущего x
и ведомого z
вала неоднозначна. Каждому положению
ведущего вала x
соответствует множество положений
ведомого вала z,
лежащего в пределах
![]()
Механическая модель.

Аналитическое описание:
![]()
Статика нелинейных систем.
Особенности характеристик соединений нелинейных звеньев.
![]()
![]() -
оператор лямбда (символ преобразования).
-
оператор лямбда (символ преобразования).
Входная величина
![]() преобразуется в выходную величину
преобразуется в выходную величину
![]() в соответствии с нелинейным дифференциальным
уравнением, описывающим динамику
нелинейного элемента, и может быть
обозначена оператором преобразования
.
в соответствии с нелинейным дифференциальным
уравнением, описывающим динамику
нелинейного элемента, и может быть
обозначена оператором преобразования
.

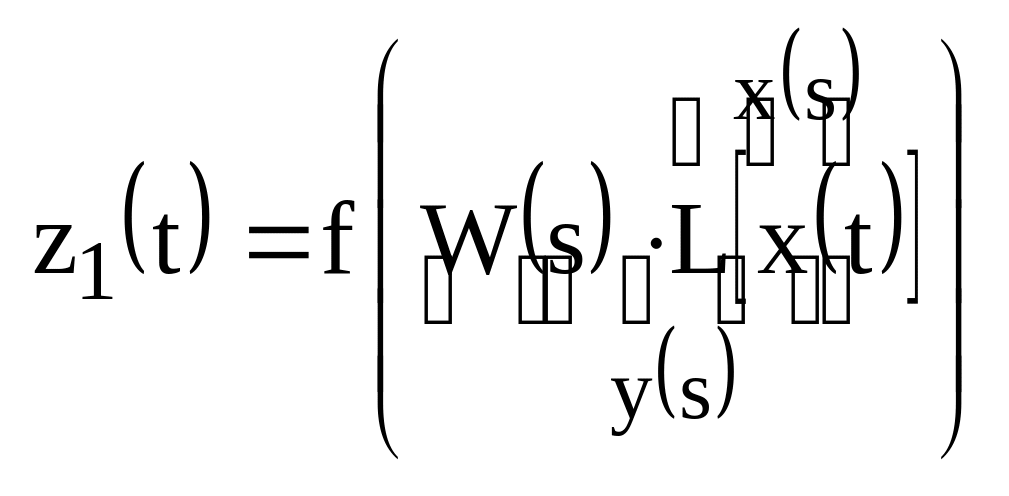
Преобразование
сигнала
![]() может быть представлено в виде
последовательного воздействия линейного
оператора
может быть представлено в виде
последовательного воздействия линейного
оператора
![]() ,
выражающего динамические свойства
звена, и нелинейного оператора
,
выражающего динамические свойства
звена, и нелинейного оператора
![]() ,
выражающего статическое преобразование
сигнала.
,
выражающего статическое преобразование
сигнала.
2.
![]()
- линейный оператор
![]() -
нелинейный оператор
-
нелинейный оператор
![]() - прямой и обратный
преобразователь Лапласа
- прямой и обратный
преобразователь Лапласа
![]()
![]()
В случае, когда
![]() тогда
тогда
![]() .
.
В общем случае недопустима перестановка линейного и нелинейного операторов, реализующих нелинейное преобразование . Исключение – когда в качестве линейного оператора звено чистого запаздывания . Поскольку перенос звена запаздывания через нелинейное звено не изменяет свойств системы.
![]()
![]()
При рассмотрении
статики нелинейных систем величины x
и z
не зависят от времени, а линейное звено
может рассматриваться как приближенное
![]() .
.
Аналогично соединениям линейных звеньев будем исходить из 3-ех видов соединения:
а) последовательное НЛЗ
б) параллельное согласное НЛЗ
в) параллельное встречное НЛЗ
а) Последовательное соединение звеньев.
![]()
![]()
![]()
![]()
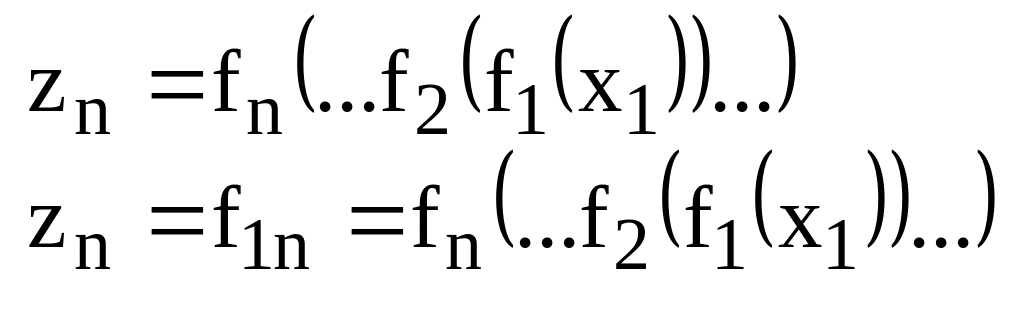
Построим графически
![]() при заданных характеристиках
при заданных характеристиках
![]() и
и
![]() .
При построении в 4-ех квадрантах в 3-ем
удобно воспроизвести
.
При построении в 4-ех квадрантах в 3-ем
удобно воспроизвести
![]() ,
дополнительную характеристику (прямая
под 45),
которая облегчает переход от
,
дополнительную характеристику (прямая
под 45),
которая облегчает переход от
![]() в характеристике
в характеристике
![]() к оси
в характеристике
к оси
в характеристике
![]()
![]()
![]()
![]()
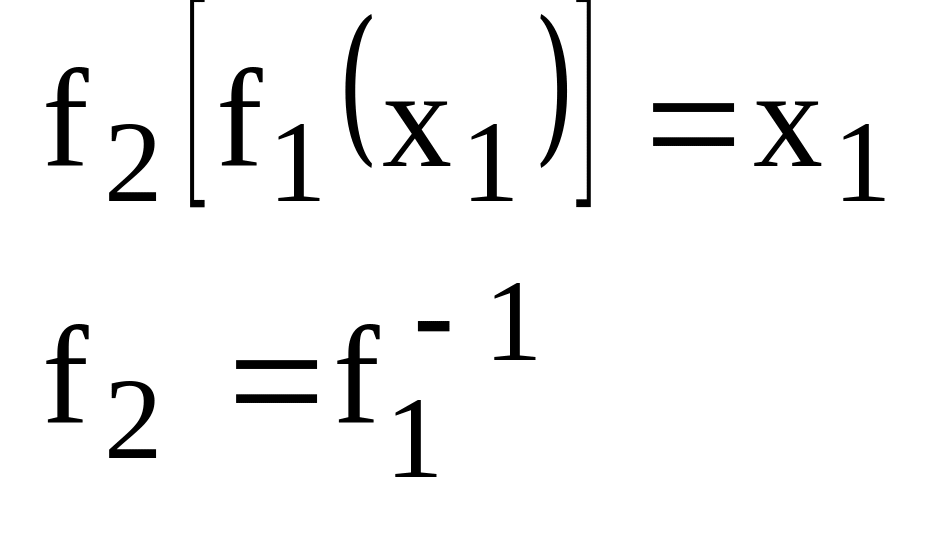
![]() - такие звенья
называются взаимообратными.
- такие звенья
называются взаимообратными.
![]()
Последовательное действие взаимообратных звеньев эквивалентно действию линейного элемента с коэффициентом усиления =1.
kобщ=1
б) Параллельное согласное соединение.

В результате графического наложения может показаться, что результат линеен и kобщ=1. Такие звенья называются взаимодополнительными и для них:
![]()
![]()

Когда
![]() - эквидистанционность на оси z
относительно прямой
- эквидистанционность на оси z
относительно прямой
![]() .
.
в) Параллельно-встречное соединение.

![]()
условия формирования параллельно-встречного соединения