Работа перемещения проводника с током в постоянном магнитном поле

Элементарная работа, совершаемая силой Ампера при малом перемещении в магнитном поле элемента тока, рассчитывается следующим образом

.

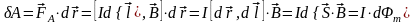При малом перемещении в магнитном поле проводника конечной длины с постоянным током I силы Ампера совершают работу

A = I ·dФ _m,

где dФ _m  магнитный поток сквозь поверхность, которую описывает проводник при его малом перемещении.

Работа сил Ампера при перемещении в магнитном поле замкнутого контура с постоянным током I рассчитывается по формуле

A_1-2 = I  = INФ_m,

где – изменение потокосцепления контура при перемещении; N  количество витков контура; Ф_m  магнитный поток через поверхность контура. Все приведенные соотношения справедливы, если в проводниках поддерживается постоянная сила тока при любых перемещениях.

22, явление электромагнитной индукции.

Электромагнитная индукция. Основной закон электромагнитной индукции

Закон электромагнитной индукции (закон Фарадея – Максвелла)

ЭДС электромагнитной индукции в контуре численно равна скорости изменения магнитного потока сквозь поверхность, натянутую на этот контур, т. е.

.

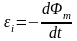Закон электромагнитной индукции можно также записать в форме

,

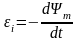где _потокосцепление электрической цепи.

Знак «минус» в выражении для ЭДС индукции объясняется правилом Ленца

«При всяком изменении магнитного потока сквозь поверхность, натянутую на замкнутый проводящий контур, в контуре возникает индукционный ток такого направления, что его собственное магнитное поле противодействует изменению магнитного потока, вызвавшему индукционный ток» (рис. 2.18).

Я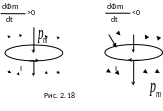 вление электромагнитной индукции в неподвижном замкнутом проводнике объясняется тем, что переменное магнитное поле вызывает появление вихревого электрического поля, циркуляция напряжённости которого вдоль замкнутого проводящего контура L равна ЭДС электромагнитной индукции

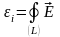_вихр.d = .

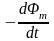Явление электромагнитной индукции в проводнике, движущемся в постоянном магнитном поле, объясняется действием силы Лоренца: разделение зарядов в проводнике (т.е. создание ЭДС) производится составляющей силы Лоренца, параллельной проводнику; составляющая, перпендикулярная проводнику, тормозит его движение (поэтому необходимо прикладывать внешнюю силу для создания ЭДС). Работа силы Лоренца в целом равна нулю.

23, взаимная ЭМИ.

Взаимная электромагнитная индукция

Взаимной индукцией называется явление возникновения ЭДС электромагнитной индукции в одной электрической цепи при изменении электрического тока в другой цепи или при изменении взаимного расположения этих двух цепей.

ЭДС взаимной индукции, возникающая во второй цепи вследствие изменения потокосцепления ₂₁ взаимной индукции этой цепи и другой (первой) цепи с током, рассчитывается по формуле

.

Потокосцепление ₂₁ обусловлено магнитным полем тока I₁ в первой цепи и, при прочих равных условиях, пропорционально силе тока I₁

_ L₂₁I₁,

где L₂₁  взаимная индуктивность второго и первого контуров (цепей). В отсутствие ферромагнетиков она зависит от размеров и формы контуров, их взаимного расположения, магнитной проницаемости среды и не зависит от силы тока. Если контуры находятся в неферромагнитной среде, то L₁₂ = L₂₁. Если L₁₂=L₂₁=const, то ЭДС взаимной индукци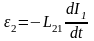и

и .

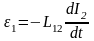24. самоиндукция.