1. два вида электричекого заряда

Закон сохранения электрического заряда

Алгебраическая сумма электрических зарядов тел или частиц, образующих электрически изолированную систему, не изменяется при любых процессах, происходящих в этой системе.

Закон Кулона

Сила электрического взаимодействия двух точечных электрических зарядов, находящихся в вакууме, прямо пропорциональна произведению этих зарядов, обратно пропорциональна квадрату расстояния между зарядами и направлена вдоль прямой, соединяющей заряды (рис. 1.1).

,

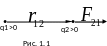
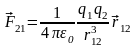Напряженность электрического поля равна силе, действующей со стороны поля на положительный единичный точечный заряд, помещённый в данную точку поля, В/м.

.

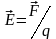Напряжённость электрического поля системы зарядов равна геометрической сумме напряжённостей полей каждого из зарядов в отдельности.

,

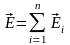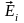
где  напряжённость поля i-го заряда системы в рассматриваемой точке пространства, n  общее число дискретных зарядов системы.

Потенциал какой-либо точки электростатического поля численно равен работе, совершаемой силами поля при перемещении положительного единичного заряда из данной точки в точку поля, где потенциал принят равным нулю.

Циркуляция вектора напряженности электростатического поля равна нулю:

потенциал электрического поля системы зарядов равна алгеобраической сумме каждого из зарядов в отдельности.

2 Напряженность и потенциал поля точечного заряда.

принципа суперпозиции

Напряжённость электрического поля системы зарядов равна геометрической сумме напряжённостей полей каждого из зарядов в отдельности.

Заряды могут быть распределены в пространстве либо дискретно, либо непрерывно. В первом случае напряжённость поля для системы точечных зарядов

,

где  напряжённость поля i-го заряда системы в рассматриваемой точке пространства, n  общее число дискретных зарядов системы.

Принцип суперпозиции для потенциала

,

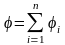т.е. при наложении электростатических полей их потенциалы складываются алгебраически.

Работа А, совершаемая кулоновскими силами при малом перемещении 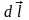точечного заряда q в электростатическом поле:

,

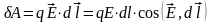где 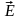 напряжённость поля в месте нахождения заряда q. Работа кулоновской силы при перемещении заряда q из точки 1 в точку 2 не зависит от формы траектории движения заряда (т.е. кулоновские силы являются консервативными силами). Работа сил электростатического поля при перемещении заряда q вдоль любого замкнутого контура L равна нулю. Это можно записать в виде теоремы о циркуляции вектора напряженности электростатического поля.

Циркуляция вектора напряженности электростатического поля равна нулю:

.

Потенциалом электростатического поля называется скалярная физическая величина , равная потенциальной энергии W_П положительного единичного точечного заряда, помещённого в рассматриваемую точку поля, В.

.

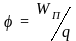Потенциал поля точечного заряда q в вакууме

.

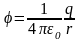Принцип суперпозиции для потенциала

,

т.е. при наложении электростатических полей их потенциалы складываются алгебраически.

Потенциал какой-либо точки электростатического поля численно равен работе, совершаемой силами поля при перемещении положительного единичного заряда из данной точки в точку поля, где потенциал принят равным нулю.

При изучении электростатических полей в каких-либо точках важны разности, а не абсолютные значения потенциалов в этих точках. Поэтому выбор точки с нулевым потенциалом определяется только удобством решения данной задачи. Связь между потенциалом и напряжённостью имеет вид

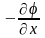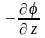Е_х = , Е_у = , Е_z = и ,

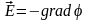т.е. напряжённость электростатического поля равна по модулю и противоположна по направлению градиенту потенциала.

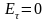Геометрическое место точек электростатического поля, в которых значения потенциалов одинаковы, называется эквипотенциальной поверхностью. Если вектор направлен по касательной к эквипотенциальной поверхности, то и . Это означает, что вектор напряженности перпендикулярен эквипотенциальной поверхности в каждой точке, т.е. E = E_n.

3. Поток вектора напряженности. . Поток напряжённости. Теорема Гаусса для электростатического поля в вакууме

Элементарным потоком напряжённости электрического поля сквозь малый участок площадью dS поверхности, проведённой в поле, называется скалярная физическая величина

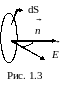
dN = 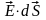= EdScos( 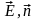) = E_ndS = EdS_,

где — вектор напряжённости электрического поля на площадк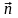е dS,  единичный вектор, нормальный к площадке dS, 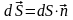 вектор площадки, Е_n = Ecos( )  проекция вектора на направление вектора , dS_ = dScos( )  площадь проекции элемента dS поверхности на плоскость, перпендикулярную вектору (рис. 1.3).

Теорема Гаусса

Поток напряжённости электростатического поля в вакууме сквозь произвольную замкнутую поверхность пропорционален алгебраической сумме электрических зарядов, охватываемых этой поверхностью:

,

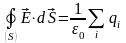4. работа сил электростатического поля по перемещению заряда.

Работа А, совершаемая кулоновскими силами при малом перемещении точечного заряда q в электростатическом поле:

,

где  напряжённость поля в месте нахождения заряда q. Работа кулоновской силы при перемещении заряда q из точки 1 в точку 2 не зависит от формы траектории движения заряда (т.е. кулоновские силы являются консервативными силами). Работа сил электростатического поля при перемещении заряда q вдоль любого замкнутого контура L равна нулю. Это можно записать в виде теоремы о циркуляции вектора напряженности электростатического поля.

Циркуляция вектора напряженности электростатического поля равна нулю:

.

Это соотношение, выражающее потенциальный характер электростатического поля, справедливо как в вакууме, так и в веществе.

Работа А, совершаемая силами электростатического поля при малом перемещении точечного заряда q в электростатическом поле, равна убыли потенциальной энергии этого заряда в поле:

А= - dW_П и А₁₂= - W_П = W_П1 - W_П2,

где W_П1 и W_П2  значения потенциальной энергии заряда q в точках 1 и 2 поля. Энергетической характеристикой электростатического поля служит его потенциал.

Потенциалом электростатического поля называется скалярная физическая величина , равная потенциальной энергии W_П положительного единичного точечного заряда, помещённого в рассматриваемую точку поля, В.

.

Потенциал поля точечного заряда q в вакууме

.

Принцип суперпозиции для потенциала

,

т.е. при наложении электростатических полей их потенциалы складываются алгебраически.

Потенциал поля электрического диполя в точке С (рис. 1.2)

.

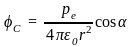Если заряды распределены в пространстве непрерывно, то потенциал  их поля в вакууме:

.

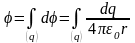Интегрирование проводится по всем зарядам, образующим рассматриваемую систему.

Работа А₁₂, совершаемая силами электростатического поля при перемещении точечного заряда q из точки 1 поля (потенциал ₁) в точку 2 (потенциал ₂):

А₁₂ = q (₁ - ₂).

Если ₂ = 0, то .

Потенциал какой-либо точки электростатического поля численно равен работе, совершаемой силами поля при перемещении положительного единичного заряда из данной точки в точку поля, где потенциал принят равным нулю.

При изучении электростатических полей в каких-либо точках важны разности, а не абсолютные значения потенциалов в этих точках. Поэтому выбор точки с нулевым потенциалом определяется только удобством решения данной задачи. Связь между потенциалом и напряжённостью имеет вид

Е_х = , Е_у = , Е_z = и ,

т.е. напряжённость электростатического поля равна по модулю и противоположна по направлению градиенту потенциала.

Геометрическое место точек электростатического поля, в которых значения потенциалов одинаковы, называется эквипотенциальной поверхностью. Если вектор направлен по касательной к эквипотенциальной поверхности, то и . Это означает, что вектор напряженности перпендикулярен эквипотенциальной поверхности в каждой точке, т.е. E = E_n.

5. поляризация диэлектриков.

Существуют два основных вида однородных и изотропных диэлектриков:

1) неполярные диэлектрики (атомы и молекулы таких диэлектриков в отсутствие внешнего электрического поля не имеют дипольных моментов, а при помещении в электрическое поле приобретают индуцированные дипольные моменты, пропорциональные величине напряженности поля);

2) полярные диэлектрики (атомы и молекулы таких диэлектриков в отсутствие внешнего электрического поля обладают дипольными моментами, при помещении в электрическое поле дипольные моменты ориентируются преимущественно по направлению вектора напряженности поля).

Поляризованность равна электрическому дипольному моменту единицы объема диэлектрика:

.

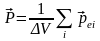Вещества, которые не проводят электрический ток, называются диэлектриками. В диэлектриках, в отличие от проводников, нет свободных носителей заряда. Все молекулы диэлектрика электрически нейтральны. Тем не менее, молекулы обладают электрическими свойствами. В первом приближении молекулу можно рассматривать как электрический диполь с дипольным электрическим моментом .

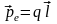Как всякий электрический диполь молекула создаёт электрическое поле, поэтому электрические поля диполей, складываясь, создают некоторое собственное поле 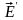, которое, налагаясь на внешнее поле , образует результирующее электрическое поле в диэлектрике .
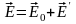