Линиатура растра?
Для характеристики изображений, которые создаются методом дизеринга, используют термин линиатура растра. Линиатура вычисляется как количество линий (ячеек) на единицу длины – сантиметр, миллиметр, дюйм. В последнем случае единицей измерения для линиатуры является lpi (по аналогии с dpi).
Реализация дизеринга в графической системе?
Как реализовать метод дизеринга в графической системе? Рассмотрим примеры преобразования растрового изображения размером p x q с определенной глубиной цвета в другой растр, предназначенный для отображения с помощью графического устройства, в котором используется ограниченное количество основных цветов. В таком случае нужно выбрать размеры ячейки т x п, которые обеспечивают достаточное количество цветовых градаций. Затем каждый пиксел растра превращается в пиксел растра отображения. Это можно осуществить двумя способами.
Первый способ. Каждый пиксел заменяется ячейкой из т x п пикселов. Это самое точное преобразование по цветам, но размер растра увеличивается и равен mp x nq пикселов.
Второй способ. Размер растра в пикселах не изменяется, если пиксел растра отображения образовывается следующим образом:
1.Определяем координаты пиксела (х, у) для преобразуемого растра.
2.Находим цвет пиксела (х, у).
3.По цвету пиксела находим номер (k) ячейки, наиболее адекватно представляющей этот цвет.
4.По координатам (х, у) вычисляем координаты пиксела внутри ячейки: xk = x mod m; yk = y mod n.
5.Находим цвет (С) пиксела ячейки с координатами (xk, yk).
6.Записываем в растр отображения пиксел (х, у) с цветом С.
Такой способ можно использовать не для любых вариантов расположения пикселов в ячейках. Конфигурации пикселов должны быть специально разработаны для таких преобразований. Одно из требований можно сформулировать так. Если ячейки разработаны на основе двух цветов, например, белого и черного, а градации изменяются пропорционально номеру ячейки, то необходимо, чтобы ячейка с номером (i) для более темной градации серого содержала бы все черные пикселы ячейки номер (i - 1).
Диагональные растры?
Для улучшения восприятия изображения можно использовать не квадратный растр а иное расположение ячеек, например, диагональное. Подобное расположение можно получить, если сдвигать четные строки ячеек (рис. 3.7).
Рис. 3.7. Пример диагонального расположения ячеек
Координаты пикселов ячеек можно вычислять следующим образом:
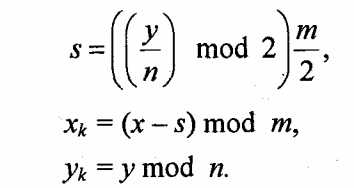
Для того чтобы получить диагональную структуру растра подобную той, что используется для печати газет, можно использовать квадратное расположение ячеек, но иного типа, нежели представленные раньше, которое при рассмотрении нескольких пикселов также дает диагональную структуру (рис. 3.8).
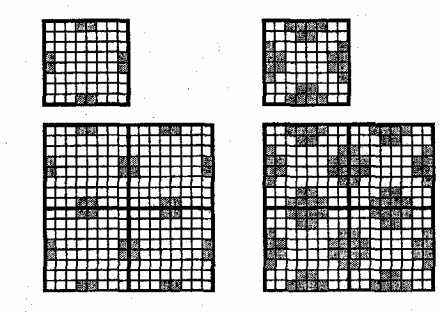
Рис. 3.8. Диагональная структура, полученная без смещения строк
Можно заметить, что для всех приведенных выше примеров дизеринга ячейки образовывают точки переменного размера с постоянным шагом.
Частотная модуляция?
Часто используется иной подход – переменная густота расположения точек постоянного размера. Такой способ получил название частотной модуляции (ЧМ) (рис. 3.9).
Рис. 3.9. Частотная модуляция для ячеек 6 х 6
Положительная черта способа ЧМ – меньшая заметность структуры растра. Однако его использование затруднено в случае, когда размер пикселов больше, чем их шаг. Начиная с определенной густоты, пикселы смыкаются. Кроме того, на дискретном растре невозможно обеспечить плавное изменение густоты (частоты), в особенности для ячеек небольшого размера. Рассмотрим пример ячеек 5х5, реализующих ЧМ-дизеринг (рис. 3.10).
Рис. 3.10. Набор ЧМ-ячеек 5 х 5
Для изображений, созданных методом ЧМ-дизеринга, наблюдается меньшая заметность растровой структуры. Однако при регулярном расположении одинаковых ячеек всегда образовывается текстура, муар, лишние контуры. Одна из важных задач – разработка таких вариантов ячеек, которые предопределяют наименее заметную растровую структуру (кроме тех случаев, когда, наоборот, такую структуру нужно подчеркнуть для создания изображения в стиле гравюры).
Один из способов создания достаточно качественных изображений – это диффузный дизеринг (diffused dithering). Суть его в том, что ячейки создаются случайно (или псевдослучайно). Если для каждой градации создавать случайные ячейки, то даже для фрагмента растра пикселов с постоянным цветом не будут образовываться регулярные структуры. Это соответствует диффузному отражению света от матовой поверхности.