Свойство функции количественной невидимости в особых точках?
Какими свойствами обладает функция v(x) на линиях складки проектирования (или контурных линиях) в случае поверхности общего положения? Можно показать, что функция v(x) может менять свое значение на линиях складки лишь в двух типах точек (рис. 12.12):
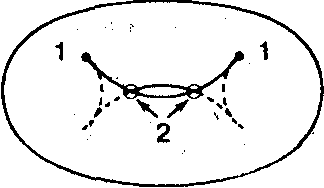
Рис. 12.12.
А. В точках, проекции которых являются пересечением, или самопересечением, проекций линий складки на картинную плоскость (в этих точках функция v(x) имеет скачок, кратный 2).
Б. В точках сборки отображения проектирования (в этих точках v(x) меняется на 1).
Первый случай достаточно очевиден: участок поверхности загораживается складкой другого участка поверхности.
Второй случай менее прост (и потому более интересен). В окрестности точек сборки проектирования поверхность загораживает сама себя и потому изменение значения функции v(x) происходит, казалось бы, без видимой причины (рис. 12.13).
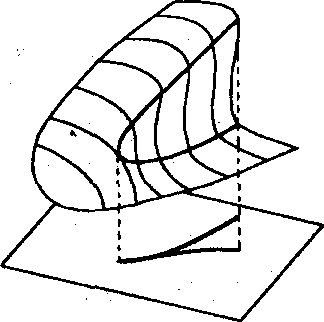
Рис. 12.13.
Отметим, что при решении задачи загораживания для многогранных поверхностей геометрические соображения, связанные с функцией видимости, также можно использовать. Функция видимости на многогранниках обладает свойствами, аналогичными рассмотренным выше. правда, анализ несколько усложняется.
Алгоритмы, использующие понятие количественной невидимости, в отличие от алгоритмов "грубой силы" имеют линейные характеристики временной сложности от разрешения поверхности, что является неулучшаемым по порядку результатом для алгоритмов, работающих в объектном пространстве. Однако в результате работы такого алгоритма получается контурное изображение, что предполагает в дальнейшем его наполнение видимыми каркасными линиями или полутоновой закраской. Это составляет отдельную задачу машинной графики. Для ее решения используются свойства функции v(x) в точках, являющихся прообразами регулярных значений отображения проектирования.
Такие точки образуют на поверхности открытое множество. Так как функция v(x) локально постоянна на этом множестве, то на всякой его связной компоненте она постоянна. Вычисляя значение функции v(x) в некоторой точке x0 и выявляя все точки, лежащие в той же компоненте связности, мы последовательно определим видимость всех участков поверхности.