84. Алгоритм удаления невидимых граней выпуклого многогранника?

В случае, если многогранник является выпуклым, коэффициенты A_i, B_i и C_i легко выбрать так, чтобы вектор n_i = (A_i, B_i, C_i) был вектором внешней нормали. Для этого найдем какую-либо внутреннюю точку многогранника W, например его барицентр:

где Р₁, Р₂,... Р_m, - множество всех вершин многогранника; и положим

и , далее,

Положительное R₊ и отрицательное R_-. по отношению к грани F_i полупространства определяются соответственно неравенствами

Сформулируем условия, определяющие, является ли грань лицевой. В случае центрального проектирования грань F_i, является лицевой, если

L_i(р) > 0, и нелицевой, если L_i (p) < 0.

В случае ортогонального проектирования грань F_i, - лицевая, если (n_i, l) > 0,

и нелицевая, если (n_i, l) < 0.

85. Количественная невидимость?

Рассмотрим на поверхности целочисленную функцию, значение которой в точке поверхности определяется как количество закрывающих ее точек. Эта функция называется функцией количественной невидимости точки и обозначается через v(x).

Обозначим через f(x) отображение проектирования гладкой поверхности S на картинную плоскость R².

Точка поверхности называется регулярной точкой отображения f, если она вместе с некоторой своей малой окрестностью проектируется взаимно однозначно на картинную плоскость, и нерегулярной, если это условие не выполнено (рис. 12.7).

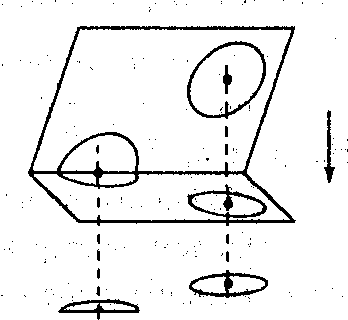
Рис. 12.7.

Множество всех нерегулярных точек отображения f естественным образом распадается на связные компоненты, каждая из которых, как правило, имеет структуру гладкой кривой, лежащей на поверхности. Эти кривые часто называют контурными линиями. Видимые части контурных линий составляют очертания любого предмета (рис. 12.8).

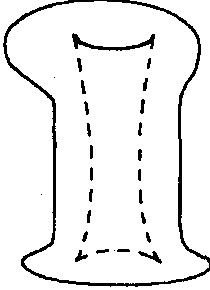
Рис. 12.8.

86. Общие свойства функции количественной невидимости?

Если поверхность находится "в общем положении", то отображение проектирования имеет лишь "типичные особенности" - линии складки (представляющие собой регулярные кривые на поверхности, взаимно однозначно проектирующиеся на картинную плоскость) и изолированные точки сборки, которые лежат на линиях складки и являются особыми точками проектирования линии складки на картинную плоскость. Подчеркнем, что в точках сборки сама линия складки не имеет особенностей. Особенность имеет отображение проектирования (рис. 12.9).

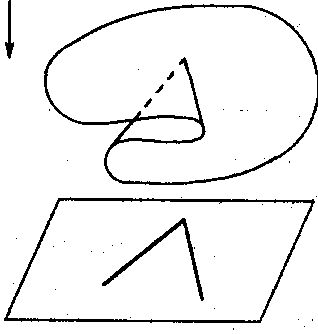
Рис. 12.9.

Возникает вопрос: насколько "типичным" является случай общего положения поверхности по отношению к проектированию на картинную плоскость? В теории особенностей гладких отображений доказывается, что всякую поверхность можно привести в общее положение сколь угодно малым "шевелением", если же поверхность находится в общем положении, то никакое достаточно малое шевеление поверхности не может испортить этого свойства.

Понаблюдав за изменением видимости при движении точки по поверхности, можно выявить следующие свойства функции v(x) (рис. 12.10).

А. Функция v(x) является локально постоянной во всех точках поверхности, на которых отображение проектирования f принимает регулярные значения, т. е. в

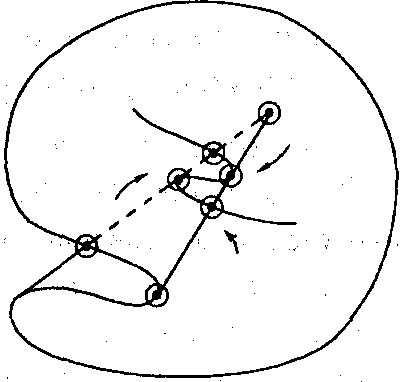
Рис. 12.10.

прообразе значения v(x) нет нерегулярных точек отображения f.

Б. Функция v(x) меняет скачком свое значение только в окрестности точек поверхности, проектирующихся на проекции контурных линий (состоящих из точек складок проектирования).

Эти наблюдения позволяют свести задачу загораживания на гладкой поверхности к анализу взаимного расположения элемента поверхности и ее контурных линий. Впрочем, дальнейшие рассмотрения показывают, что и этот анализ избыточен и достаточно изучить функцию v(x) лишь на контурных линиях поверхности. Для этого, в свою очередь, нужно исследовать взаимное расположение линий, состоящих из точек складок проектирования на поверхности при отображении проектирования (рис. 12.11.).

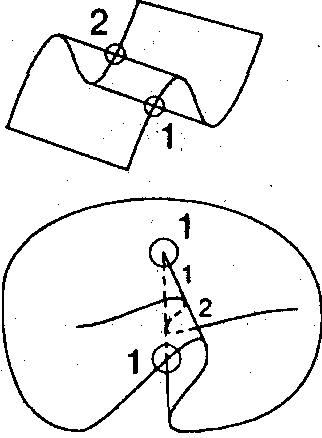
Рис. 12.11.