Сортировка граней по глубине?
Для удаления невидимых граней воспользуемся методом упорядоченного вывода граней. В данном случае треугольники выводятся не по мере удаления от картинной плоскости, а по мере их приближения, начиная с дальних и заканчивая ближними: треугольники, расположенные ближе к плоскости экрана, выводятся позже и закрывают собой невидимые части более дальних треугольных граней так, что если данный пиксель накрывается сразу несколькими гранями, то в этом пикселе будет видна грань, ближайшая к картинной плоскости (рис. 11.7).
Рис. 11.7
В результате применения описанной процедуры мы получаем правильное изображение поверхности.
Для определения
порядка, в котором должны выводиться
грани, воспользуемся тем, что треугольники,
лежащие в полосе
не могут закрывать треугольники из
полосы
.
Таким образом, грани можно выводить по
полосам, по мере их приближения к
картинной плоскости. Данный метод носит
название сортировки
граней по глубине.
Метод z-буфера?
Метод Z-буфера основывается на использовании дополнительного массива (буфера в памяти), в котором хранятся координаты Z для каждого пикселя растра. Координата Z отвечает расстоянию точек пространственных объектов до плоскости проектирования. Например, она может быть экранной координатой в системе экранных координат, если ось OZ перпендикулярна плоскости экрана.
Положим теперь, что чем ближе точка в пространстве к плоскости проецирования, тем больше значение Z. Тогда сначала Z-буфер заполняется минимальными значениями. Потом начинается вывод всех объектов. Причем порядок вывода объектов в этом методе значения не имеет. Во время вывода каждого пиксела по его координатам (X, Y) находится текущее значение Z в Z-буфере. Если рисуемый пиксел имеет большее значение, чем значение Z в Z-буфере, то это означает, что данная точка ближе к объекту. В этом случае пиксел действительно рисуется, а его Z-координата записывается в Z-буфер. Таким образом после рисования всех пикселов растровое изображение будет состоять из тех пикселов, которые соответсвуют точкам объектов с самыми большими координатами Z, то есть – видимые точки, расположенные ближе всего к наблюдателю.
Эвристические концепции невидимости?
Рассмотрим простые эвристические соображения, которые могут служить отправной точкой для решения задачи загораживания.
А. Пусть сцена разбита на два фрагмента - А и В. Если самые дальние точки фрагмента А лежат ближе к наблюдателю, чем самые ближние точки фрагмента В, то части В, очевидно; никак не могут загородить фрагмента А. Поэтому, если мы сначала построим изображение фрагмента В, а затем изображение фрагмента А, то в результате получим правильное изображение всей сцены. Тем самым мы устанавливаем приоритет, в соответствии с которым нужно производить обработку исходных данных для получения целостного изображения (рис.12.1).
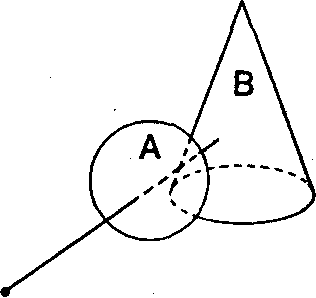
Рис.12.1.
Б. Предложим несколько иной способ вычисления приоритетов отдельных фрагментов сцены. Пусть в объектном пространстве нам удалось найти плоскость, которая разделяет все пространство на такие два полупространства, в одном из которых находятся фрагмент А и наблюдатель, а в другом - фрагмент В. Ясно, что при этих условиях фрагмент В не может загораживать фрагмент А.
В качестве примера рассмотрим сцену, состоящую из двух непересекающихся шаров. В данном случае разделяющая плоскость строится легко: она проходит через точку отрезка, соединяющую центры шаров перпендикулярно ему (рис. 12.2). Остается лишь узнать, в какое полупространство попал наблюдатель.
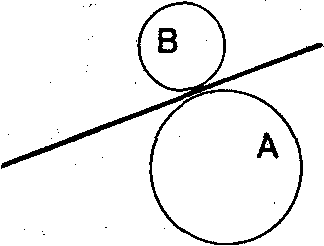
Рис.12.2.
Если непересекающиеся фрагменты А и В выпуклы, то, как известно, разделяющая плоскость обязательно имеется. Если же фрагменты А и В невыпуклые, то можно попытаться поместить их в непересекающиеся выпуклые тела (например, в шары возможно меньших радиусов), что в случае успеха позволит свести задачу к предыдущему более простому случаю. Так же можно поступить и при вычислении расстояний до наблюдателя (см. А).
В. Предыдущие примеры показывают, что полезно установить, при каких условиях обработка одного из фрагментов сцены, скажем А, может производиться позже, чем обработка другого фрагмента, и при этом изображение в целом останется правильным. Полезно также знать, когда два фрагмента могут обрабатываться независимо друг от друга. Даже если у нас нет
средств для параллельных вычислений, решение задачи загораживания подобных случаях все равно заметно упрощается. Например, если проекции фрагментов А и В на картинную плоскость не пересекаются, то обработка каждого из них может производиться независимо.
Общая задача о пересечении проекций произвольных объектов весьма сложна, однако использование простых достаточных условий не пересечения часто оказывается полезным. Например, описав вокруг проекций прямоугольники со сторонами, параллельными осям координат, и убедившись, что они не пересекаются (это сведется к проверке нескольких неравенств), мы можем быть уверены, что исходные фигуры также не пересекаются. Правила вычисления приоритета или установления факта независимости фрагментов должны быть достаточно простыми, иначе "средство" не оправдает "цель".
Г. Заметим, что высказанные выше соображения можно применить для построения каждого из фрагментов А и В: нужно только разбить фрагмент А на подфрагменты А' и А", а фрагмент В - на В' и В" и снова применить описанную выше процедуру. Идея этого метода состоит в применении общего принципа, известного под названием "разделяй и властвуй". Вместо решения одной сложной задачи рекурсивно решается серия простых задач. Задача дробится до тех пор, пока ситуация не упростится настолько, что ее можно будет разрешить на основе простых правил (рис. 12.3).
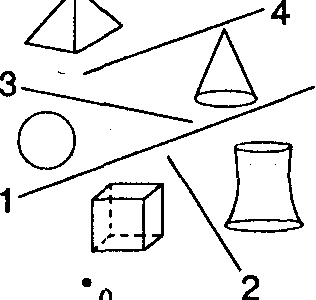
Рис.12.3.
Д. Вместо того, чтобы расчленять сцену, можно попытаться разбивать картинную плоскость и обрабатывать независимо те части изображения, которые попадают в соответствующие фрагменты картинной плоскости. Принцип тот же, что и выше (см. Г), только анализ производится не в объектном пространстве, а на плоскости изображения.
Е. Нетрудно заметить, что свойства сцены связаны со свойствами изображения на картинной плоскости, и поэтому их стоит учитывать при выборе метода решения задачи загораживания.