Задача удаления невидимых линий и поверхностей?
Одной из важнейших задач трехмерной графики является определение того, какие части объектов (ребра, грани), находящиеся в трехмерном пространстве, будут видны, а какие будут закрыты от наблюдателя другими объектами. В качестве возможных видов проектирования традиционно рассматривается параллельное и центральное.
Само проектирование осуществляется на экран, который в данном случае и представляет собой картинную плоскость; через каждую точку объекта проводится проектирующий луч (проектор) к картинной плоскости (Рис.11.1).
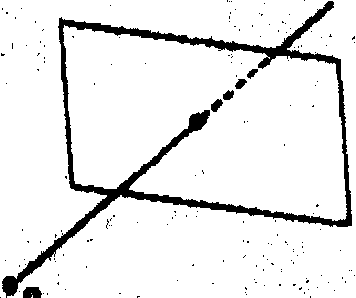
Рис. 11.1.
Все проекторы образуют пучок либо параллельных лучей (при параллельном проектировании) либо лучей, выходящих из одной точки (центральное проектирование). Пересечение проектора с картинной плоскостью дает проекцию точки. Видимыми будут только те точки, которые вдоль направления проектирования расположены ближе всего к картинной плоскости. Все три точки P1, P2, P3 (Рис. 11.2) лежат на одном и том же проекторе, но так как точка P1 лежит ближе к картинной плоскости, чем точки P2, P3, и закрывает их при проектировании, то из этих трех точек именно она одна является видимой.
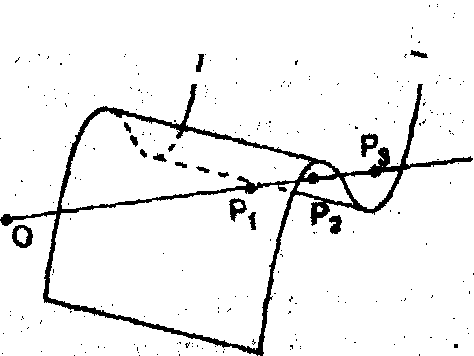
Рис.11.2.
Несмотря на кажущуюся простоту, задача удаления невидимых линий и поверхностей является достаточно сложной и зачастую требует очень больших объемов вычислений. Поэтому существует целый ряд различных методов решения этой задачи, включая и методы, опирающиеся на аппаратные решения.
Эти методы различаются по следующим основным параметрам:
способу представления объектов;
способу визуализации сцены;
пространству, в котором производится анализ видимости;
виду получаемого результата (его точности).
Общие характеристики методов удаления невидимых линий и поверхностей?
В качестве возможных способов представления объектов могут выступать аналитические способы (явные и неявные), параметрические и полигональные.
Далее будем считать, что все объекты представлены набором выпуклых плоских граней, например треугольников (полигональный способ), которые могут пересекаться одна с другой только вдоль ребер.
Координаты в исходном трехмерном пространстве будем обозначать через (х, у, z), а координаты в картинной плоскости - через (X, Y). Будем также считать, что на картинной плоскости задана целочисленная растровая решетка - множество точек (i, j), где i, j - целые числа.
Если это не оговорено особо, будем считать для простоты, что проектирование осуществляется на плоскость Оху. Проектирование при этом происходит либо парраллельно,оси Оz, т. е. задается формулами
X = x; Y = y
либо является центральным с центром, расположенным на оси Oz, и задается формулами
Существуют два различных способа изображения трехмерных тел - каркасное (wireframe - рисуется только .ребра) и сплошное (рисуются закрашенные грани). Тем самым возникают два типа задач. - удаление, невидимых линий (ребер для каркасных изображений) и удаление невидимых поверхностей (граней .для сплошных изображений)
Анализ видимости, объектов можно производить как в исходном трехмерном пространстве, так и на картинной плоскости. Это приводит к разделению методов на два класса:
методы, работающие непосредственно в пространстве самих объектов;
методы, работающие в пространстве картинной плоскости, т.е. работающие с проекциями объектов.
Получаемый результат представляет собой либо набор видимых областей или отрезков, заданных с машинной точностью (имеет непрерывный вид), либо информацию о ближайшем объекте для каждого пикселя экрана (имеет дискретный вид). Методы первого класса дают точное решение задачи удаления невидимых линий поверхностей, никак не привязанное к растровым свойствам картинной плоскости. Они могут работать как с самими объектами, выделяя те их части, которые видны, так и с их проекциями на картинную плоскость, выделяя на ней области, соответствующие проекциям видимых частей объектов, и, как правило, практически не привязаны к растровой решетке и свободны от погрешностей дискретизации. Так как эти методы работают с непрерывными исходными данными и получающиеся результаты не зависят от растровых свойств, то их иногда называют непрерывными (continuous methods).
Простейший вариант непрерывного подхода заключается в сравнении каждого объекта со всеми остальными, что дает временные затраты, пропорциональные n2, где n - количество объектов в сцене. Однако следует иметь ввиду, что непрерывные методы, как правило, достаточно сложны.
Методы второго класса (point-sampling methods) дают приближенное решение задачи видимости, определяя видимость только в некотором наборе точек картинной плоскости – в точках растровой решетки. Они очень сильно привязаны к растровым свойствам картинной плоскости и фактически заключаются в определении для каждого пикселя той грани, которая является ближайшей к нему вдоль направления проектирования. Изменение разрешения приводит к необходимости полного перерасчета всего изображения.
Простейший вариант дискретного метода имеет временные затраты порядка С где С - общее количество пикселей экрана, a n - количество объектов.
Всем методам второго класса традиционно свойственны ошибки дискретизации (aliasing artifacts). Однако, как правило, дискретные методы отличаются известной простотой.
Кроме этого существует довольно большое количество смешанных методов, использующих работу как в объектном пространстве, так и в картинной плоскости, методы, выполняющие часть работы с непрерывными данными, а часть - с дискретными.
Большинство алгоритмов удаления невидимых граней и поверхностей тесно связано с различными методами сортировки. Некоторые алгоритмы проводят сортировку явно, в некоторых она присутствует в скрытом виде. Приближенные методы отличаются друг от друга фактически только порядком и способом проведения сортировки.
Очень распространенной структурой данных в задачах удаления невидимых линий и поверхностей являются различные типы деревьев - двоичные (BSP-trees), четвертичные (Quadtrees), восьмеричные (Octtrees) и др.
Методы, практически применяющиеся в настоящее время, в большинстве являются комбинациями ряда простейших алгоритмов, неся в себе целый ряд разного рода оптимизаций.