61. Векторная полигональная модель?

Для описания пространственных объектов здесь используются такие элемен ты: вершины; отрезки прямых (векторы); полилинии, полигоны; полигональные поверхности (рис. 9.2).

Элемент "вершина" (vertex) – главный элемент описания, все другие являются производными. При использовании трехмерной декартовой системы координаты вершин определяются как (x_i, y_i, z_i). Каждый объект однозначно определяется координатами собственных вершин.

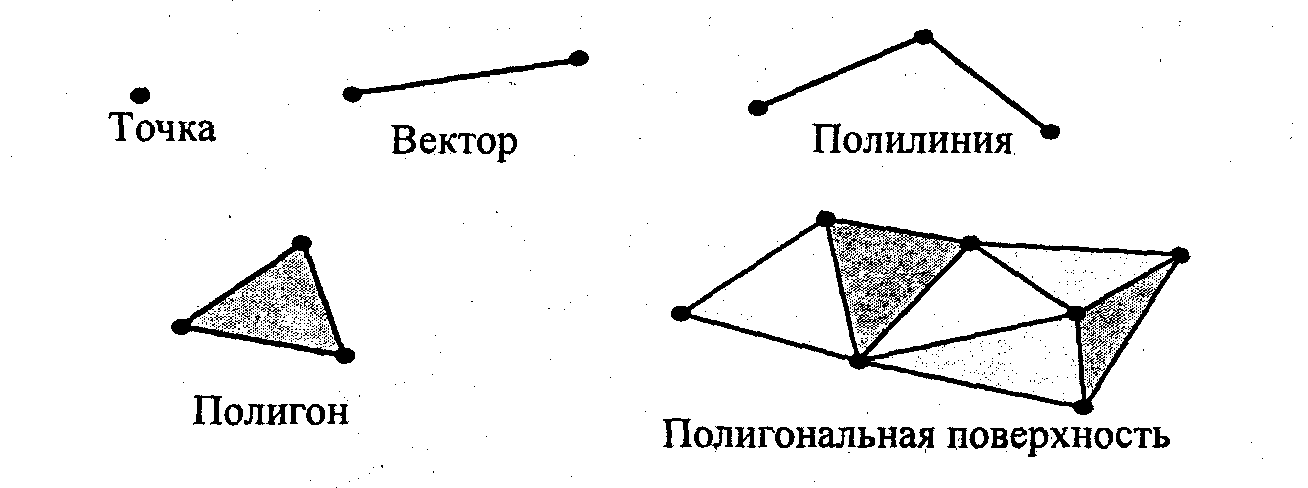
Рис. 9.2. Базовые элементы векторно-полигональной модели '

Вершина может моделировать отдельный точечный объект, размер которое не имеет значения, а также может использоваться в качестве конечных точек для линейных объектов и полигонов. Двумя вершинами задается вектор. Несколько векторов составляют полилинию. Полилиния может моделировать отдельный линейный объект, толщина которого не учитывается, а также может представлять контур полигона. Полигон моделирует площадный объект. Один полигон может описывать плоскую грань объемного объекта. Несколько граней составляют объемный объект в виде полигональной поверхности – многогранник или незамкнутую поверхность (в литературе часто употребляется название "полигональная сетка").

Векторную полигональную модель можно считать наиболее распространен ной в современных системах трехмерной КГ. Ее используют в системах автоматизированного проектирования, в компьютерных играх и тренажерах в САПР, геоинформационных системах и тому подобное.

Рассмотрим на примере куба структуры данных, которые используются в векторной полигональной модели. Описание такого объекта в структурах данных можно описать следующими способами.

62. Первый способ описания структур данных в векторной модели?

В первом способе при описании все грани куба сохраняются в отдельности (рис. 9.3).

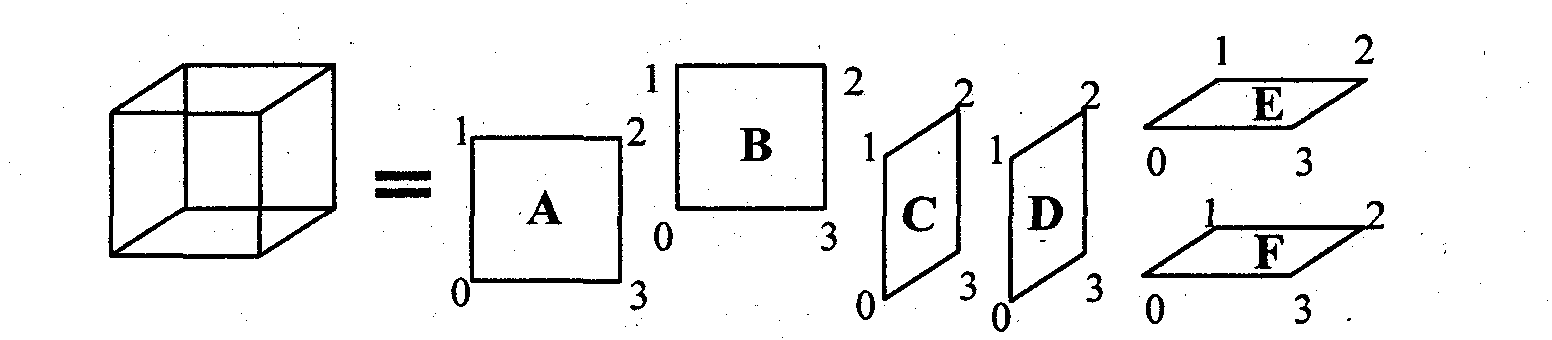
Рис. 9.3. Первый способ описания куба

Тогда грань A - это кортеж из 4-х троек координат:

{ (x_ао, у_ао, z_ао), (x_а1, у_а1, z_а1), (x_а2, у_а2, z_а2), (x_а3, у_а3, z_а3) }

Остальные грани определяются аналогично. Например, грань B задается как:

{ (x_Bо, у_Bо, z_Bо), (x_B1, у_B1, z_B1), (x_B2, у_B2, z_B2), (x_B3, у_B3, z_B3) }

С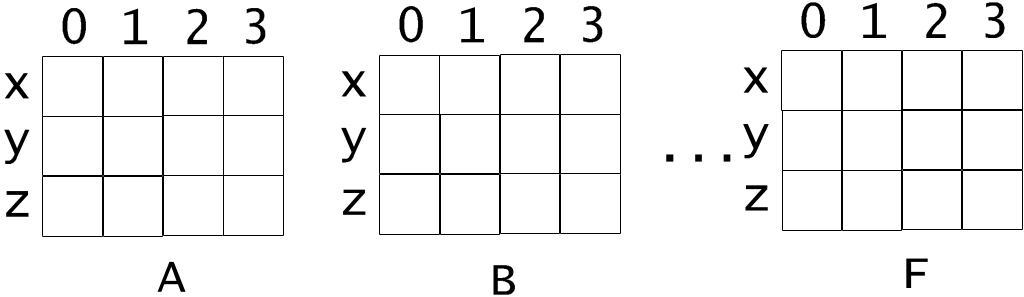 хематично это видно на рис. 9.4.

Рис. 9.4. Отдельные грани

В компьютерной программе такой способ описания объекта можно реализовать разнообразно. Например, для каждой грани открыть в памяти отдельный массив. Можно все грани записывать в один массив-вектор. А можно использовать классы (языком C++) как для описания отдельных граней, так и объектов в целом. Можно создавать структуры, которые объединяют тройки (x, у, z), или сохранять координаты отдельно. В значительной мере это относится уже к компетенции программиста.

Если внимательно посмотреть на вышеприведенный способ описания, то можно отметить, что каждая из вершин (во всяком случае в кубе) описывается трижды – так как она принадлежит сразу трем смежным граням

63. Второй и третий способы описания структур данных в векторной модели?

В торой вариант описания не содержит повторов. Вершины пронумерованы, например, как на рис 9.5

Рис. 9.5. Куб с пронумерованными вершинами

А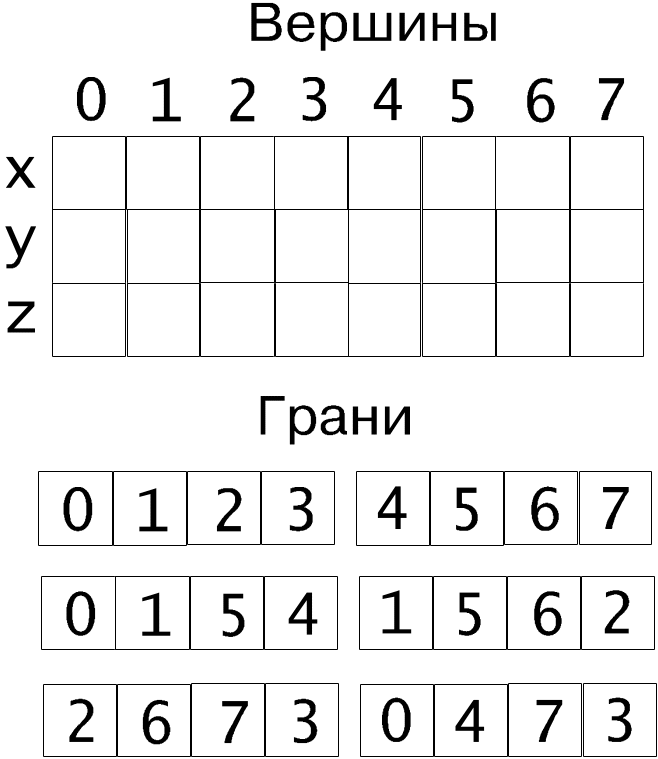 каждая грань дается в виде списка указателей на вершины (рис. 9.6)

Рис. 9.6. Индексы вершин в массивах граней.

Третий способ известен под названием линейно-узловой модели и основывается на иерархии: вершины – ребра – грани (рис. 9.7).

При построении подобных моделей большую роль играет скорость вывода полигонов. Если для того, чтобы изобразить полигоны нужно нарисовать линию контура и точки заполнения, то первый и второй варианты близки по скорости. Отличие лишь в том, что для второго варианта нужно сначала выбирать индекс вершины, что замедляет процесс вывода. Для третьего варианта можно предусмотреть такой способ рисования контура, чтобы каждая линия рисовалась только один раз (помечать уже нарисованную линию). Это обусловливает преимущество третьего варианта по быстродействию.

Представим теперь, что мы поменяли координаты одной вершины (рис 9.8.)

Что произойдет в этом случае? Если использовался второй или третий способы, где каждая вершина присутствует в одном экземпляре, изменение ее координат приведет автоматически к изменению всех граней, в описании которых п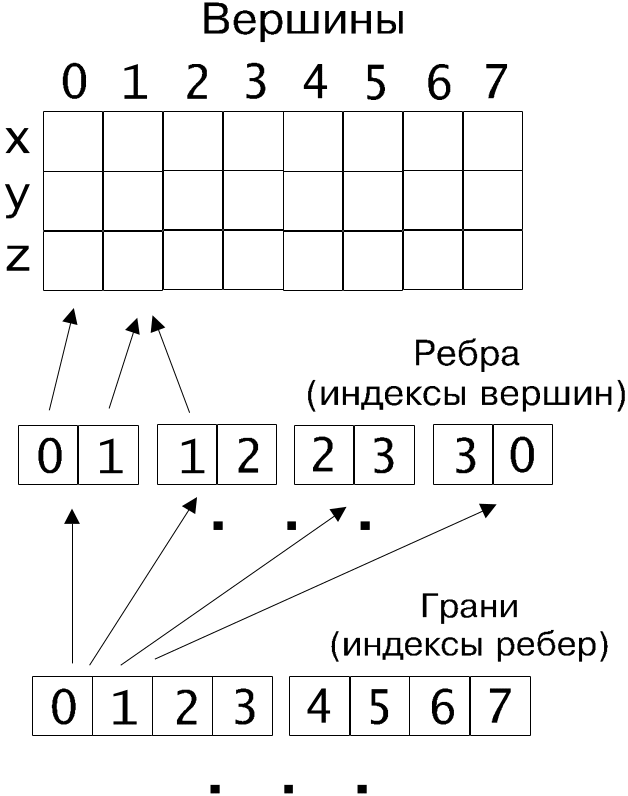 рисутствует индекс этой вершины.

Рис. 9.7. Линейно-узловая модель

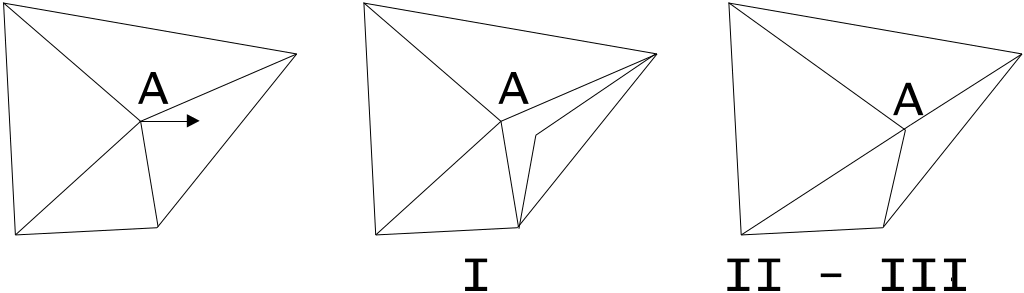
Рис.9.8.Результат изменения координат одной вершины (по вариантам).

В первом же варианте картинка исказится, поскольку добавятся новые грани. Однако, когда нужно разъединить смежные грани, то для второго и третьего вариантов это сложнее, чем для первого – необходимо дополнить структуру данных новой вершиной, новыми ребрами и определить индексы в массивах граней.