58. Аналитическая модель описания поверхности?

Аналитической моделью будем называть описание поверхности математическими формулами. В КГ можно использовать много разновидностей такого описания. Например, в виде функции двух аргументов z = f (x, у). Можно использовать уравнение F (x, у, z) = 0.

Зачастую используется параметрическая форма описания поверхности. Запишем формулы для трехмерной декартовой системы координат (x, у, z):

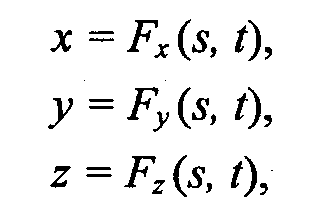
где s и t – параметры, которые изменяются в определенном диапазоне, а функции Fx, Fy и Fz будут определять форму поверхности. '

Преимущества параметрического описания – легко описывать поверхности, которые отвечают неоднозначным функциям, замкнутые поверхности. Описание можно сделать таким образом, что формула не будет существенно изменяться при поворотах поверхности, масштабировании.

В качестве примера рассмотрим аналитическое описание поверхности шара Сначала как функцию двух аргументов:

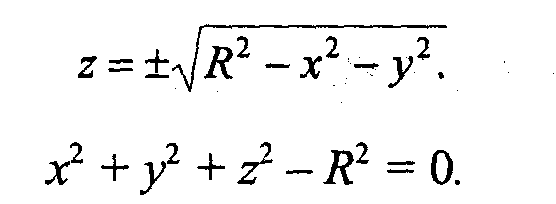
А также в параметрической форме:

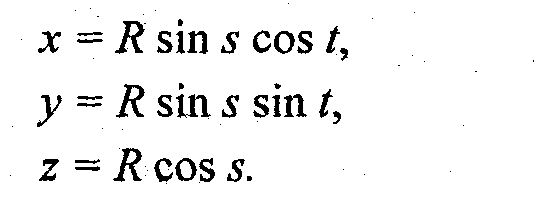
59. Аппроксимация сплайна?

Для описания сложных поверхностей часто используют сплайны. Сплайн – это специальная функция, более всего пригодная для аппроксимации отдельных фрагментов поверхности. Несколько сплайнов образовывают модели сложной поверхности. Другими словами, сплайн – эта тоже поверхность, на такая, для которой можно достаточно просто вычислять координаты ее точек.

60. Кубический сплайн?

Для описания сложных поверхностей часто используют сплайны. Сплайн – это специальная функция, более всего пригодная для аппроксимации отдельных фрагментов поверхности. Несколько сплайнов образовывают модели сложной поверхности. Другими словами, сплайн – эта тоже поверхность, на такая, для которой можно достаточно просто вычислять координаты ее точек. Обычно используют кубические сплайны. Почему именно кубические? Потому, что третья степень – наименьшая из степеней, позволяющих описывать любую форму, и при стыковке сплайнов можно обеспечить непрерывную первую производную – такая поверхность будет без изломов в местах стыка. Сплайны часто задают параметрически. Запишем формулу для компоненты x(s, t) кубического сплайна в виде многочлена третьей степени параметров s и t:

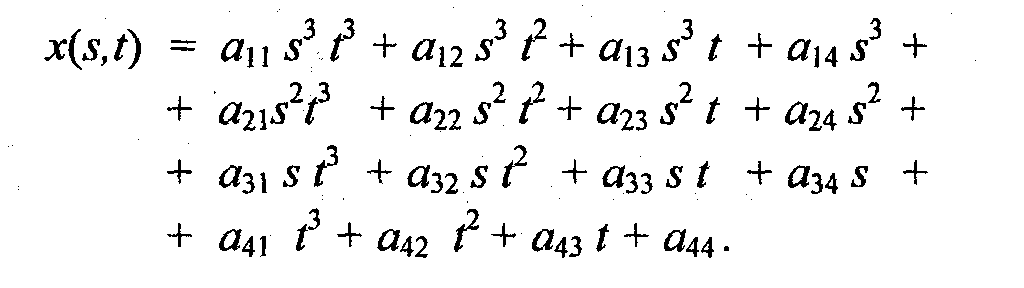
В математической литературе можно ознакомиться со способами определения» коэффициентов Оу для сплайнов, которые имеют заданные свойства.

Интерполяционным кубическим сплайном называется функция S(x), обладающая следующими свойствами:

1) S(x_i) = y_i, i = 0,1,…,N (N + 1 – количество опорных точек для построения кривой).

2)[x_i, x_{i + 1}]:

;

3) На всем отрезке [x₀, x_N] функция S(x) имеет непрерывную вторую производную.

Так как на каждом из отрезков [x_i, x_{i + 1}] сплайн S(x) определяется четырьмя коэффициентами, то для его полного построения на всем отрезке задания необходимо найти 4N чисел. Для выполнения третьего условия достаточно потребовать непрерывности сплайна во всех внутренних узлах x_i i = 1,…,N-1 (это дает N-1 условие на коэффициенты), а также его первой (еще N-1 условие) и второй (и еще N-1 условие) производных в этих узлах. Всего с первым требованием получаем 4N – 2 равенства. Недостающие два условия можно получить, задав, к примеру значения первых производных на концах отрезка [x₀, x_N]:

S’(x₀) = l₀, S’(x_N) = l_N.

Аналогично строятся сплайны и в трехмерном случае, но здесь они носят название бикубических.

Рассмотрим еще одну из разновидностей сплайнов – сплайн Безье. Приведем его сначала в обобщенной форме – степени m x n:

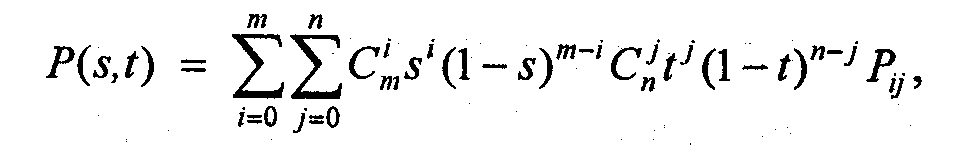
где Pij – опорные точки-ориентиры, 0  s  l, 0  t  1, C_mⁱ , и С_n^j –коэффициенты бинома Ньютона, они рассчитываются по формуле:

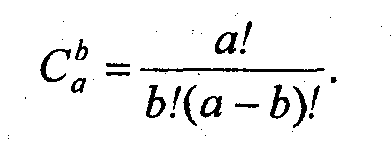
Кубический сплайн Безье соответствует значениям т = 3, п = 3. Для его определения необходимо 16 точек-ориентиров Pij (рис. 9.1); коэффициенты C_mⁱ, С_n^j равны 1,3,3,1 при i,j =0,1,2,3.

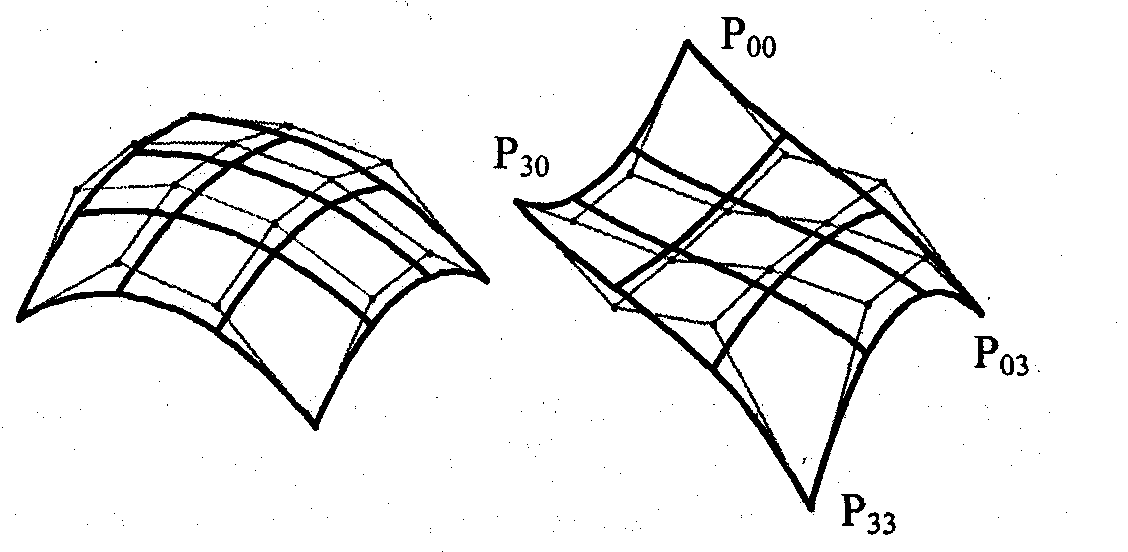
Рис. 9.1. Кубические сплайны Безье

Характеризуя аналитическую модель в целом» можно сказать, что эта модель наиболее пригодна для многих операций анализа поверхностей. С позиций КГ можно указать такие положительные черты модели: легкая процедура расчета координат каждой точки поверхности, нормали; небольшой объем информации для описания достаточно сложных форм.

К недостаткам относятся следующие: сложные формулы описания с использованием функций, которые медленно вычисляются на компьютере, снижают скорость выполнения операций отображения; невозможность в большинстве случаев применения данной формы описания непосредственно для построения изображения поверхности. В таких случаях поверхность отображают как многогранник, используя формулы аналитического описания для расчета координат вершин граней в процессе отображения, что уменьшает скорость по сравнению с, например, полигональной моделью описания.