Алгоритм закрашивания линиями?
Алгоритм закрашивания линиями. получил широко распространение в компьютерной графике. От приведенного ранее простейшего рекурсивного алгоритма он отличается тем, что на каждом шаге закрашивания рисуется горизонтальная линия, которая размещается между пикселами контура. Алгоритм рекурсивный, но поскольку вызов функции осуществляется для линии, а не для каждого отдельного пиксела, то количеств вложенных вызовов уменьшается пропорционально длине линии. Это уменьшает нагрузку на стековую память компьютера. Приведем алгоритм рекурсивной функции закрашивание линиями:
Функция ЗАКРАШИВАНИЕ_ЛИНИИ(x, y, dir, preXL, preXR)
{
xl = x;
xr = x; //выбор начальной точки
Выполнять цикл пока clr <> Border_Color
{
clr = ЦВЕТ_ПИКСЕЛ(xl-1, y)
}
Выполнять цикл пока clr <> Border_Color
{
clr = ЦВЕТ_ПИКСЕЛ(xr+1, y)
}
xl = xl + 1;
xr = xr – 1;
ЛИНИЯ(xl, y) – (xr +1, y);
Выполнять цикл по x от xl до xr
{
clr = ЦВЕТ_ПИКСЕЛ(x, y+dir);
Если clr <> Border_Color то
x = ЗАКРАШИВАНИЕ_ЛИНИИ(x, y+dir, dir, xl, xr);
}
Выполнять цикл по x от xl до preXL-1
{
clr = ЦВЕТ_ПИКСЕЛ(x, y-dir);
Если clr <> Border_Color то
x = ЗАКРАШИВАНИЕ_ЛИНИИ(x, y-dir, -dir, xl, xr);
}
Выполнять цикл по x от preXR до xr-1
{
clr = ЦВЕТ_ПИКСЕЛ(x, y-dir);
Если clr <> Border_Color то
x = ЗАКРАШИВАНИЕ_ЛИНИИ(x, y-dir, -dir, xl, xr);
}
ВОЗВРАТ xr
}
Пример работы алгоритма закрашивания линиями приведен на рис. 7.4.
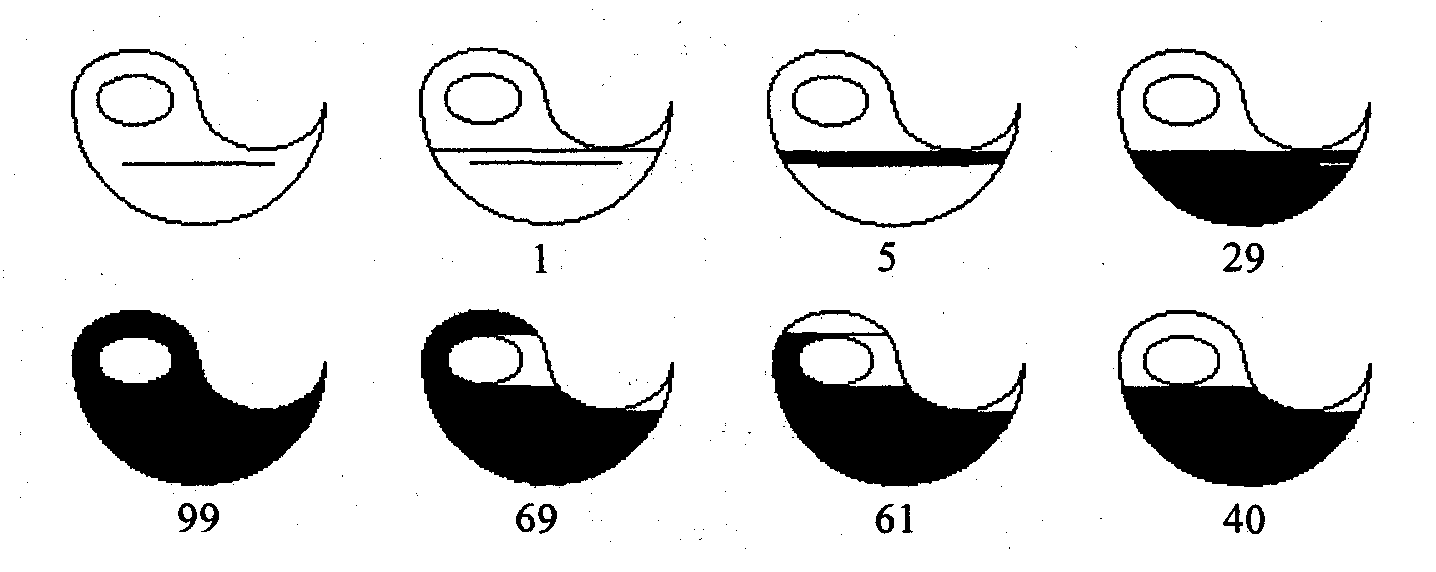
Рис. 7.4. Количество циклов при закрашивании линиями
Заполнение прямоугольника и круга?
Среди всех фигур прямоугольник заполнять наиболее просто. Если прямоугольник задан координатами противоположных углов, например, левого верхнего (х1, у1) и правого нижнего (х2, у2), тогда алгоритм может заключаться в последовательном рисовании горизонтальных линий заданного цвета (рис. 7.5).
Рис. 7.5. Заполнение прямоугольника
Для заполнения круга можно использовать алгоритм Брезенхэма для окружности, который рассматривался ранее В процессе выполнения этого алгоритма последовательно вычисляются координаты пикселов контура в границах одного октанта. Для заполнения надлежит выводить горизонтали, которые соединяют пары точек на контуре, расположенные симметрично относительно оси у (рис. 7.6).
Так же может быть построен и алгоритм заполнения эллипса.
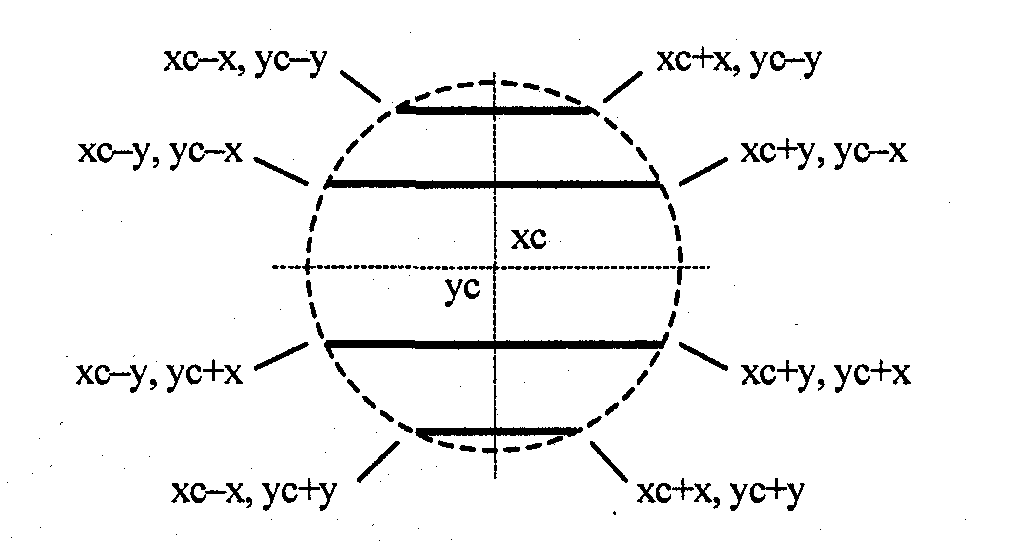
Рис. 7.6. Заполнение круга
Заполнение полигонов?
Контур полигона определяется вершинами, которые соединены отрезками прямых (рис. 7.7). Это – векторная форма задания фигуры.
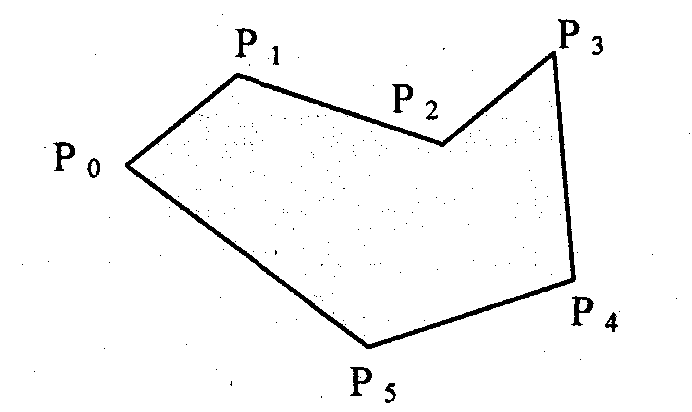
Рис. 7.7. Пример полигона
Рассмотрим один из наиболее популярных алгоритмов заполнения полигона, основная идея которого состоит в закрашивании фигуры отрезками прямых линий. Наиболее удобно использовать горизонтали. Алгоритм представляет собою цикл вдоль оси у, в ходе этого цикла выполняется поиск точек сечения линии контура с соответствующими горизонталями. Этот алгоритм получил название «ХУ»:
Шаг 1. Найти min(yi) и max(yi) среди всех вершин Pi.
Шаг 2. Выполнить цикл по у от у = min до у = max.
Шаг 3. Нахождение точек пересечения всех отрезков контура с горизонталью у.
Координаты хj точек сечения записать в массив X.
Шаг 4. Сортировка массива X по возрастанию х.
Шаг 5. Вывод горизонтальных отрезков с координатами
(х0, у) - (х1, у)
(х1, у) - (х2, у)
………………
(х2k, у) - (х2k+1, у)
Каждый отрезок выводится цветом заполнения
В этом алгоритме использовано свойство топологии контура фигуры. Оно;
состоит в том, что любая прямая линия пересекает любой замкнутый контур четное количество раз (рис. 7.8). Для выпуклых фигур точек пересечения с любой прямой всегда две. Таким образом, на шаге 3 этого алгоритма в массив x всегда должно записываться парное число точек сечения.
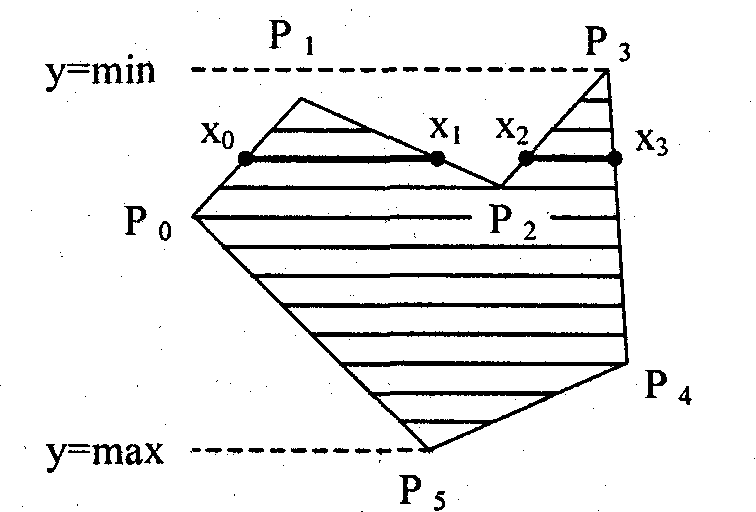
Рис.7.8. Заполнение полигона •