47. Построение эллипса?

Уравнение эллипса имеет вид:

или

.

В силу симметрии эллипса относительно координатных осей достаточно найти растровое представление только для одной из его четвертей, лежащей в квадранте координатной плоскости: x  0, y  0.

Разобьем четверть эллипса на две части: 1 - ту где угловой коэффициент касательной к нему лежит между –1 и 0, и 2 - ту, где угловой коэффициетн меньше –1 (рис.6.4).

Р ис.6.4.Четверть эллипса с касательной и нормалью

Вектор нормали к касательной в точке (x, y) имеет вид:

.

В точке, разделяющей части эллипса с разными угловыми коэффициентами,

.

Поэтому y-компонента градиента в 1-й части больше x-компоненты. Во 2-й области – наоборот. Таким образом, если в следующей срединной точке

то мы переходим из области 1 в область 2.

Вычислим теперь, как и при построении окружности значение функции F для потенциально возможных следующих точек и используем знак этой функции, чтобы определить, лежит ли средняя точка внутри эллипса или вне его.

Если текущий пиксел для 1-й части равен (x_i, y_i), то

.

При d_i < 0 полагаем y_{i + 1} = y_i и

При d_i  0 полагаем y_{i + 1} = y_i + 1 и

Если текущий пиксел для 2-й части равен (x_i, y_i), то

,

а все дальнейшие выкладки аналогичны 1-му случаю.

2-я часть начинается в точке (0, b) и первая средняя точка имеет координаты (1, b – ½). Поэтому начальной выбирается точка

.

Отметим, чтоо здесь на каждой итерации не только проверяется знак d_i но и вычисляется градиент в средней точке, с помощью которого отслеживается, не пора ли переходить в часть 2.

48. Кривая Безье?

Большое семейство линий представляют собой так называемые кривые Безье, названные так по имени разработавшего их математика. Кривые Безье описываются в параметрической форме:

P_x(t) и P_н(t) – многочлены, зависящие от параметра t и имеющие вид:

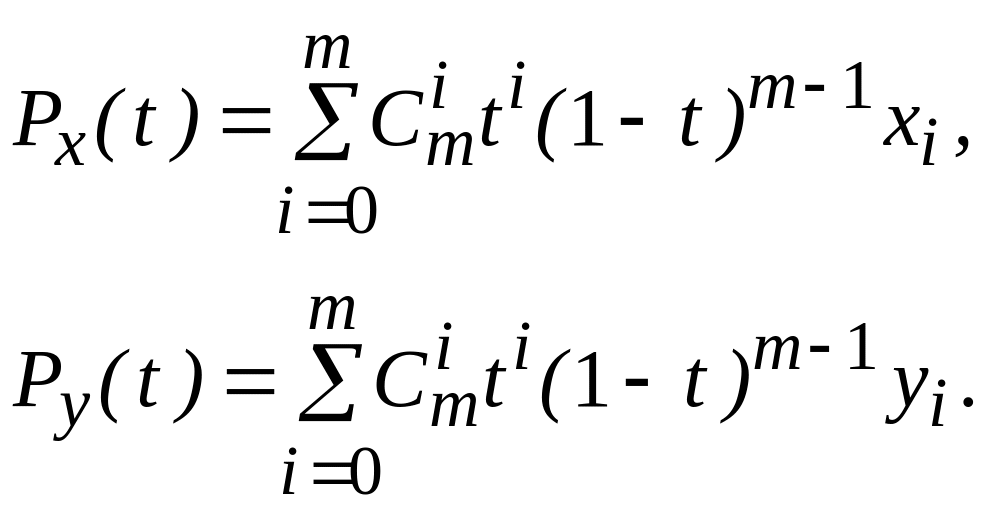
где - число сочетаний из m элементов по i. Напомним, что

,

а x_i и y_i – координаты точек ориентиров P_i . Значения m рассматриваются как степень полинома, при этом m должно быть на единицу меньше, чем количество точек - ориентиров. Таким образом при m = 1 кривая Безье строится по 2-м точкам. Понятно, что при этом она вырождается в отрезок прямой, опрделеяемый концевыми точками P₀ и P₁:

.

При m = 2 кривая Безье строится по трем точкам (рис.6.5).

Р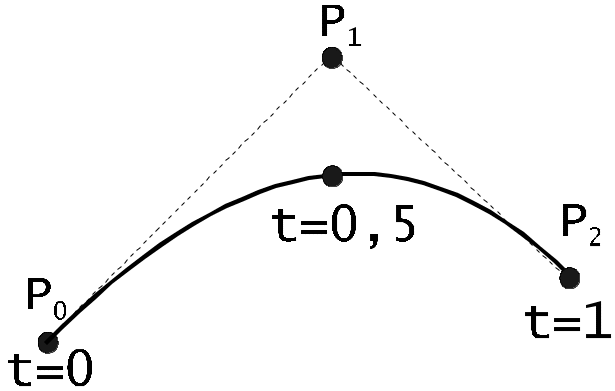 ис.6.5. Построение кривой Безье по трем точкам.

Уравнение для t [0,1] будет иметь вид:

.

Однако наиболее часто используются кубические кривые Безье, которые строятся по 4-м точкам. Уравнение такой кривой будет иметь вид:

.

49. Геометрический алгоритм?

следующий алгоритм для построения кривых Безье, называемый геометрическим. Он состоит из следующих шагов:

1. Каждая сторона контура многоугольника, проходящего по точкам - ориентирам, делится пропорционально значению t.

2. Точки деления соединяются отрезками прямых и образуют новый многоугольникю Количество узлов нового контура на единицу меньше, чем количество узлов предыдущего контура.

Рис.6.6. Кривые Безье 3-го порядка.

3. Стороны нового контура снова делятся пропорционально значению t. И так далее. Это продолжается до тех пор, пока не будет получена единственная точка деления. Она и будет точкой кривой Безье.

П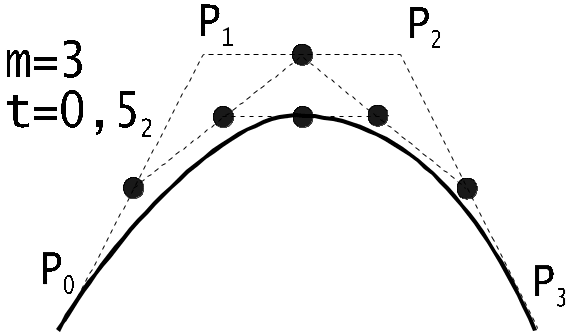 остроение показано на рис.6.7.

Рис.6.7. Геометрический алгоритм Безье.