42. Понятие соседей и связности?

Сформировать растровое изображение можно по разному. Так, можно просто скопировать готвый растрв видеопамять. Но можно создавать изображение объекта путем последовательного рисования отдельных простых элементов: линий и фигур. Такие простые элементы носят название графических примитивов (ГП).

Современные методы рисования ГП основываются на так называемых инкрементных алгоритмах, разработанных Брезенхэмом. Основной целью для разработки таких алгоритмов было построение циклов вычисления координат пикселов, образующих ГП на основе только целочисленных операций сложения/вычитания без использования умножения и деления

Инкрементные алогритмы выполняются как последовательное вычисление координат соседних пикселов путем добавления приращений координат, которые рассчитываются на основе анализа функции погрешности

Алгоритмы Брезенхэма опираются на понятия соседей и связности.

Пусть имеется квадратная сетка на плоскости с шагом 1. Узлы данной решетки являются центрами соответствующих квадратных ячеек сетки. Будем называть такую решетку растром Инициализация точки растра с координатами (i, j) означает закрашивание ее квадратной окрестности.

43. Принцип работы четырехсвязного алгоритма Брезенхэма?

Точки на плоскости называются 4-соседями, если у них отличаются только x-координаты или только y-координаты, причем только на 1.

Т.о. всякая точка на плоскости имеет 4-х непосредственных соседей и 8 косвенных соседей.

4-путем (сильносвязанным) на плоскости является множество точек, для которых две соседние точки являются 4-соседями.

44. Принцип работы восьмисвязного алгоритма Брезенхэма?

Точки на плоскости называются 8-соседями, если у них отличаются x-координаты и y-координаты, но только на 1.

8-путем (сильносвязанным) на плоскости является множество точек, для которых две соседние точки являются 8-соседями.

45. Пример восьмисьмисвязного алгоритма?

Приведем пример восьмисвязного алгоритма Брезенхэма:

xerr = 0, yerr = 0;

dx = x2 – x1, dy = y2 – y1;

Если dx > 0, то incX = 1;

dx = 0, то incX = 0;

dx < 0, то incX = -1;

Если dy > 0, то incY = 1;

dy > 0, то incY = 0;

dy > 0, то incY = -1;

dx = |dx|, dy = |dy|;

Если dx > dy, то d = dx иначе d = dy;

x = x1, y = y1;

Пиксел (x,y);

Выполнить цикл d раз:

(

xerr = xerr + dx;

yerr = yerr +dy;

Если xerr > d, то xerr = xerr – d, x = x + incX;

Если yerr > d, то yerr = yerr – d, y = y + incY;

Пиксел (x,y);

)

П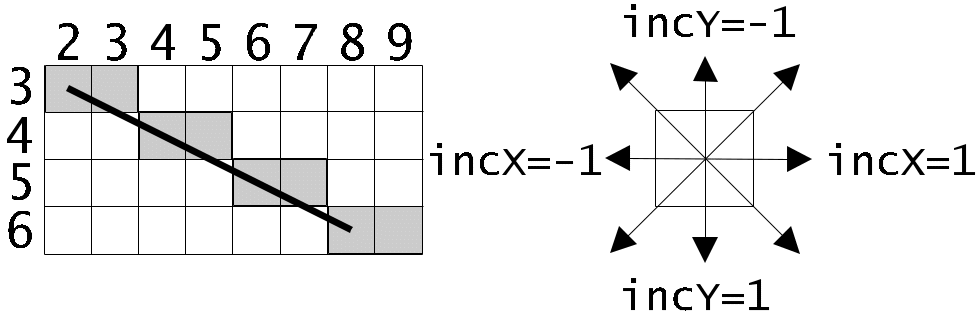 ринцип работы этого алгоритма виден из рисунка (рис. 6.1.). Алгоритм для

Рис. 6.1. Восьмисвязность

данного примера работает 7 тактов.

46. Построение окружности?

Для вывода контура окружности используется соотношение:

,

где R – радиус окружности. При этом для упрощения пользуются ее симметрией относительно координатных осей, проходящих через ее центр и прямых y =  x. Тем самым достаточно построить только 1/8 часть окружности

Рассмотрим участок окружности из 2-го октанта

.

Особенностью данного участка является то обстоятельство, что угловой коэффициент касательной к окружности не превосходит 1 по модулю, а точнее – лежит между –1 и 0.

Функия

обращается в 0 на самой окружности, отрицательна внутри окружности и положительна вне ее.

П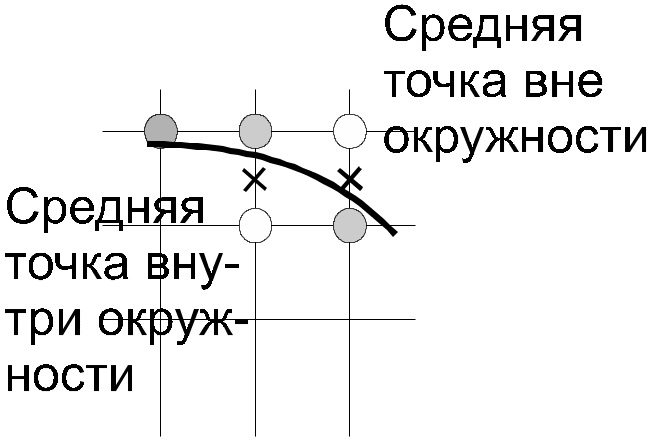 усть точка (x_i, y_i) уже поставлена (рис.6.3).

Рис.6.3. Выбор точки для рисования дуги окружности

Для определения того, какую именно точку следует взять в качестве y_i+1 введем переменную

.

В случае, когда d_i < 0 полагаем, что y_{i + 1} = y_i. Тогда

Когда d_i  0, то делаем шаг вниз, выбирая y_{i + 1} = y_i + 1. При этом

Таким образом мы определили итеративный механизм перехода от одного пиксела к другому.

В качестве стартового пиксела берется