Какая проекция называется косоугольной?
Косоугольные проекции сочетают в себе свойства ортографических проекций со свойствами аксонометрию. В этом случае проекционная плоскость перпендикулярна главной координатной оси, поэтому сторона объекта, перпендикулярная этой оси проецируется так, что углы и расстояния остаются неизменными. На других сторонах искажаются углы.
Какая проекция называется кабинетной?
Одной из самых важных косоугольных проекций является кабинетная проекция. В ней направление проецирования составляет с проекционной плоскостью 45. При этом отрезки, перпендикулярные проекционной плоскости составляют 1/2 их действительной длины.
Выписать матрицы проектирования вдоль координатных осей?
Для описания преобразований проектирования удобно пользоваться матрицами. Например, матрица проектирования на плоскость OYZ вдоль оси OX имеет следующий вид:
.
Если M(x,y,z) - заданная точка, то соответствующая ей точка на картинной плоскости находится так:
.
Таким образом точка M(x,y,z) проектируется в точку M*(0,y,z). Если плоскость проектирования параллельна координатной плоскости OYZ и отстоит от нее на расстоянии p = const вдоль оси X, то матрица проектирования будет иметь вид:
Для остальных двух координатных плоскостей нулевой элемент на главной диагонали будет соответствовать оси, вдоль которой ведется проектирование.
Какую информацию нужно задать для проективного преобразования пространственного объекта?
Пусть мы хотим применить это преобразование к единичному квадрату (рис. 23а). Тогда, рассматривая поочередно все вершины квадрата
Рис. 23. Проективное преобразование единичного квадрата.
имеем:
что и изображено на рис. 4б.
Из полученного можно сделать вывод (и доказать его), что в результате преобразования, определяемого матрицей Q, произвольная прямая параллельная оси OX, переходит в прямую, описываемую уравнением вида
,
а пучок параллельных оси абсцисс прямых преобразуется в пучок прямых, проходящих через точку (-a,0) (рис.24а, б).
Рис. 24. Преобразование пучка прямых.
Получаемая таким образом точка называется точкой схода преобразования, задаваемого матрицей Q.
Привести вид матрицы проектирования для косоугольной проекции?
В виде матрицы записываются преобразования проектирования и для случаев, когда проектирующий пучок не перпендикулярен плоскости проекции. Например, при косоугольной проекции вдоль оси OZ на плоскость OXY под углом 45 матрица будет иметь вид:
Теперь имеет смысл вновь обратиться к однородным координатам, которые мы рассматривали ранее. Чтобы лучше понять их свойства, которые не были нужны при аффинных преобразованиях, но крайне полезны при проективных преобразованиях, рассмотрим, например, преобразование плоскости, задаваемое матрицей
,где
a
= const
0.
Произвольная точка плоскости M(x,y) преобразуется по правилу
.
Чтобы вернуться к однородным координатам
,
разделим x
и y
на величину
и получим точку M*
с координатами
Выписать вид матрицы проектирования в однородных координатах и докажите, что она осуществляет проектирование в двумерные координаты?
В самом деле, переходя к однородным координатам, прямым вычислением совсем легко проверить, что
Вспоминая свойства однородных координат, запишем полученный результат в несколько ином виде:
и затем путем непосредственного сравнения убедимся в том, что это координаты той же самой точки. Отметим, что матрица проектирования, разумеется, вырожденна.
Матрица соответствующего перспективного преобразования (без проектирования) имеет следующий вид:
Обратим внимание на то, что последняя матрица не вырождена.
Рассмотрим пучок прямых, параллельных оси Z, и попробуем разобраться в том, что с ним происходит под действием матрицы Q.
Каждая прямая пучка однозначно определяется точкой (скажем, M(x, y, z)) своего пересечения с плоскостью XY и описывается уравнениями X = x, Y = y, Z = t.
Переходя к однородным координатам и используя матрицу Q, получаем:
Устремим t в бесконечность. При переходе к пределу точка (x, y, t, 1) преобразуется в (0, 0, 1, 0). Чтобы убедиться в этом, разделим каждую из координат на t.
Тем самым бесконечно удаленный (несобственный) центр (0, 0, 1, 0) пучка прямых, параллельных оси Z, переходит в точку (0, 0, -c, 1) оси Z.
Вообще каждый несобственный пучок прямых (совокупность прямых, параллельных заданному направлению), не параллельной картинной плоскости
под действием преобразования, задаваемого матрицей Q, переходит в собственный пучок
Центр этого пучка
называется точкой схода.
Принято выделять так называемые главные точки схода, которые соответствуют пучкам прямых, параллельных координатным осям.
Для преобразования с матрицей Q существует лишь одна главная точка схода. В общем случае (когда оси координатной системы не параллельны плоскости экрана) таких точек три.
Матрица соответствующего преобразования выглядит следующим образом:
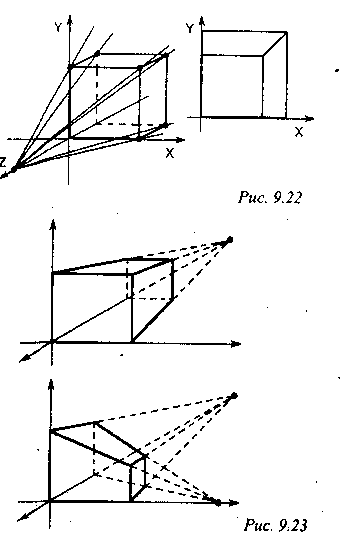
На последних рисунках изображены проекции куба со сторонами, параллельными координатным осям, с одной и с двумя главными точками схода.
Точки (-a, 0,0) и (0, -b, 0) суть главные точки схода.