Какая проекция называется ортографической?
В зависимости от взаимного расположения картинной плоскости и направления пучка прямых, осуществляющих проектирование, различают несколько случаев. Самым простым является тот, когда картинная плоскость совпадает с одной из координатных плоскостей или параллельна ей (рис. 22). Такая проекция называется ортографической. Ортографические проекции мы часто называем просто: вид сбоку, вид спереди, вид сверху.
Рис. 22. Размещение картинных плоскостей при параллельном проектировании.
Матрица проектирования вдоль оси X на плоскость YZ имеет вид:
В случае, если плоскость проектирования параллельна координатной плоскости, необходимо умножить матрицу Px на матрицу сдвига. В результате получаем
Аналогично записываются матрицы проектирования вдоль двух других координатных осей:
Отметим, что все три полученные матрицы проектирования вырожденны.
В случае аксонометрических ортографических проекций используются проекционные плоскости не параллельные координатным плоскостям, поэтому на них могут быть изображены сразу несколько сторон объекта.
В соответствии со взаимным расположением плоскости проектирования и координатных осей различают три вида проекций:
- триметрию - нормальный вектор картинной плоскости образует с ортами координатных осей попарно различные углы;
- диметрию - два угла между нормалью картинной плоскости и координатными осями равны;
- изометрию - все три угла между нормалью картинной плоскости и координатными осями равны.
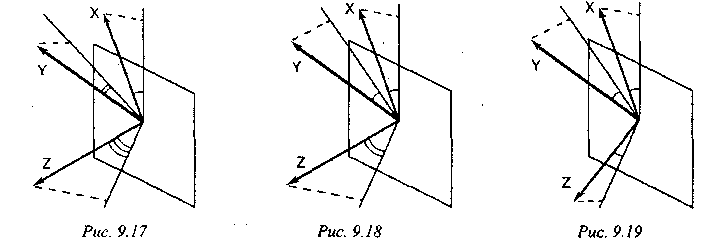
Каждый из трех видов указанных проекций получается комбинацией поворотов, за которой следует параллельное проектирование. При повороте на угол относительно оси ординат, на угол вокруг оси абсцисс и последующего проектирования вдоль оси аппликат возникает матрица
При аксонометрическом проецировании сохраняется параллельность прямых, а углы изменяются.
Какая проекция называется аксонометрической?
В случае аксонометрических ортографических проекций используются проекционные плоскости не параллельные координатным плоскостям, поэтому на них могут быть изображены сразу несколько сторон объекта.
В соответствии со взаимным расположением плоскости проектирования и координатных осей различают три вида проекций:
- триметрию - нормальный вектор картинной плоскости образует с ортами координатных осей попарно различные углы;
- диметрию - два угла между нормалью картинной плоскости и координатными осями равны;
- изометрию - все три угла между нормалью картинной плоскости и координатными осями равны.
Каждый из трех видов указанных проекций получается комбинацией поворотов, за которой следует параллельное проектирование. При повороте на угол относительно оси ординат, на угол вокруг оси абсцисс и последующего проектирования вдоль оси аппликат возникает матрица
При аксонометрическом проецировании сохраняется параллельность прямых, а углы изменяются.
Какая проекция называется изометрической?
Самым известным видом аксонометрии является изометрия, когда нормаль к проекционной плоскости (направление проецирования) составляет равные углы с каждой из главных координатных осей. Изометрическая проекция обладает следующим важным свойством: все три главные координатные оси укорачиваются одинаково. Следовательно, если выбрать масштабный множитель равный 1, то изменение длин ни по одной из этих осей не произойдет.