
- •76. Линейный криптоанализ.
- •78. Семейство алгоритма, вычисляющих хэш – функцииMd (md2, md4, md5).
- •79. Стандарт sha-1.
- •80. Цифровая подпись.
- •81. Схема подписи rsa
- •82. Верификация цифровой подписи.
- •83. Схема цифровой подписи Рабина.
- •84. Схема подписи dss.
- •Использование dsa [править]
- •85. СхемаподписиЭль – Гамаля.
- •Шифрование
- •Расшифрование
- •86. Схема подписи по гост 34.10 – 90.
- •Алгоритм Параметры схемы цифровой подписи [править]
- •Двоичные векторы [править]
- •87. Схема подписи Шнорра.
Двоичные векторы [править]
Между
двоичными векторами длины
256 ![]() и
целыми числами
и
целыми числами ![]() ставится взаимно-однозначное
соответствие по
следующему правилу
ставится взаимно-однозначное
соответствие по
следующему правилу 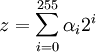 .
Здесь
.
Здесь ![]() либо
равно 0, либо равно 1. Другими словами,
либо
равно 0, либо равно 1. Другими словами, ![]() —
это двоичное представление числа z.
—
это двоичное представление числа z.
Результатом
операции конкатенации двух
векторов ![]() и
и ![]() называется
вектор длины 512
называется
вектор длины 512 ![]() .
Обратная операция — операция разбиения
одного вектора длины 512 на два вектора
длины 256.
.
Обратная операция — операция разбиения
одного вектора длины 512 на два вектора
длины 256.
Отличия от ГОСТ 34.10-94 (старый стандарт)
Новый
и старый ГОСТы цифровой подписи очень
похожи друг на друга. Основное отличие —
в старом стандарте часть операций
проводится над полем
![]() ,
а в новом — над группой точек
эллиптической кривой, поэтому требования
налагаемые на простое число
в
старом стандарте(
,
а в новом — над группой точек
эллиптической кривой, поэтому требования
налагаемые на простое число
в
старом стандарте(![]() или
или ![]() )
более жёсткие, чем в новом.
)
более жёсткие, чем в новом.
Алгоритм
формирования подписи отличается
только в пункте
4. В старом стандарте в
этом пункте вычисляются ![]() и
и ![]() и,
если
и,
если ![]() ,
возвращаемся к пункту 3. Где
,
возвращаемся к пункту 3. Где ![]() и
и ![]() .
.
Алгоритм
проверки подписи отличается только
в пункте
6. В старом стандарте в
этом пункте вычисляется ![]() ,
где
,
где ![]() —
открытый ключ для проверки подписи,
—
открытый ключ для проверки подписи, ![]() .
Если
.
Если ![]() ,
подпись правильная, иначе неправильная.
Здесь
—
простое число,
и
является
делителем
,
подпись правильная, иначе неправильная.
Здесь
—
простое число,
и
является
делителем ![]() .
.
Использование математического аппарата группы точек эллиптической кривой, позволяет существенно сократить порядок модуля , без потери криптостойкости.[1]
Также старый стандарт описывает механизмы получения чисел , и .
ВОЗМОЖНЫЕ ПРИМЕНЕНИЯ
Использование пары ключей (открытый, закрытый) для установления ключа сессии.[4]
Использование в сертификатах открытых ключей.[5]
Использование в S/MIME (PKCS#7, Cryptographic Message Syntax).[6]
Использование для защиты соединений в TLS (SSL, HTTPS, WEB).[7]
Использование для защиты сообщений в XML Signature (XML Encryption).[8]
Защита целостности Интернет адресов и имён (DNSSEC).[9]
87. Схема подписи Шнорра.
Схема Шнорра — протокол идентификации, который является альтернативой протоколам Фиата-Шамира и Гиллу-Кискатра. Надежность алгоритма основывается на сложности вычисления дискретного логарифма. Данный алгоритм позволяет проводить предварительные вычисления, что удобно при малых вычислительных ресурсах. Нужно отметить, что в протоколе передается только три сообщения. Это было сделано специально для уменьшения взаимодействия в сетях с низкой пропускной способностью.
ОПИСАНИЕ ПРОТОКОЛА:
Выбор параметров системы [править]
Выбирается простое p и простое q, такое, что
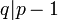 (p≈
(p≈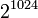 ,
, 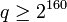 )
)Выбирается элемент β, такой, что
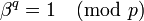
Параметры (p,q,β) свободно публикуются
Выбирается параметр t,
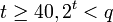 (t-уровень
секретности)
(t-уровень
секретности)
Выбор параметров доказывающей стороны [править]
Пусть каждая доказывающая сторона A выбирает секрет a (закрытый ключ), такой, что
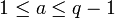 и
вычисляет
и
вычисляет  ,
где v-открытый
ключ
,
где v-открытый
ключ
Передаваемые сообщения [править]
A
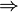 B :
B : 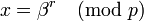
A
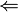 B :
e (где
B :
e (где 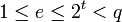 )
)A B :
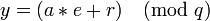
Основные действия [править]
A выбирает случайное r (
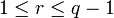 ),
вычисляет
и
отсылает x стороне
B (доказательство)
),
вычисляет
и
отсылает x стороне
B (доказательство)Сторона B отсылает случайное e из диапазона
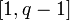 (вызов)
(вызов)A возвращает B
B проверяет, действительно ли z=x, где
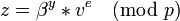 и,
если это так, то идентификация считается
успешной.
и,
если это так, то идентификация считается
успешной.
Модификация для цифровой подписи
Пусть сторона A хочет отправить сообщение М стороне B; причем B должен убедиться в том, что сообщение пришло именно от A. Тогда:
A выбирает случайное r ( ), вычисляет
Пусть имеется однонаправленная хеш-функция H(M). Сторона А объединяет M с x и хеширует результат
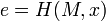
Далее A вычисляет
 .
Значения e и y являются
цифровой подписью и отсылаются B.
.
Значения e и y являются
цифровой подписью и отсылаются B.B вычисляет . Затем z и полученное сообщение M' пропускаются через хеш-функцию:
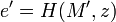 .
Если
.
Если 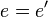 ,
то подпись считается верной.
,
то подпись считается верной.
