
- •Министерство образования и науки Российской федерации
- •«Новгородский государственный университет имени Ярослава мудрого»
- •Содержание
- •Перечень сокращений, символов и специальных терминов
- •Введение
- •Обобщеные циклотомические оследовательности
- •Основные опрЕделения
- •1.3 Обобщенные циклотомические классы по модулю
- •Вычисление линейной сложности последовательностей четвертого порядка
- •Список использованной литературы
Вычисление линейной сложности последовательностей четвертого порядка
Пусть
последовательность четвертого порядка,
то есть
 ,
тогда, согласно лемме 1.1, она формируется
по правилу:
,
тогда, согласно лемме 1.1, она формируется
по правилу:
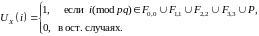 (2.1)
(2.1)
Заметим, что правило
(2.1) задает последовательность только
тогда, когда
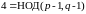 .
Здесь откажемся
от этого предположения и рассмотрим
общий случай. Таким образом, по теореме
1.1, имеем
.
Здесь откажемся
от этого предположения и рассмотрим
общий случай. Таким образом, по теореме
1.1, имеем
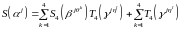 .
(2.2)
.
(2.2)
Как и в [7] из формулы (2.2) получаем следующее утверждение.
Лемма 2.1. Если
последовательность
определена по правилу (2.1), тогда для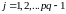 имеем
имеем

Следствие 2.1.
Значение
многочлена
 последовательности постоянно, когда
принадлежит
обобщенным циклотомическим классам ,
множествам
последовательности постоянно, когда
принадлежит
обобщенным циклотомическим классам ,
множествам
 .Пусть
.Пусть
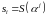 ,
когда
,
когда
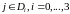 .
.
Воспользовавшись формулой (1.7) из леммы 2.1 получаем, что
 , (2.3)
, (2.3)
где
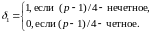 и
и

Прежде
чем приступить к вычислению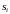 ,
введем несколько обозначений. Пусть,
далее,
,
введем несколько обозначений. Пусть,
далее,
 и
и
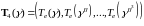 .
Определим матрицу
.
Определим матрицу
 четвертого
порядка следующим образом:
четвертого
порядка следующим образом:
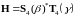 (*-
транспонирование матрицы).
(*-
транспонирование матрицы).
Лемма
2.2.Если
,
то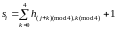 или
или
 (2.4)
(2.4)
Данная формула следует непосредственно из леммы 2.1.
Таким образом,
фактически, для расчета линейной
сложности циклотомических последовательностей
достаточно рассчитать матрицу
для этого случая. В [9] были найдены
значения
 для
для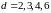 и частично для
и частично для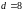 .
В частности, если
,
то всегда справедливо разложение
.
В частности, если
,
то всегда справедливо разложение
 ,
,
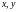 -
целые числа и
-
целые числа и
 ,
посредством которого и находятся
значения
,
посредством которого и находятся
значения
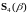 .
Согласно [9] имеют место следующие
соотношение:
.
Согласно [9] имеют место следующие
соотношение:
1.
 или
или ,
если
,
если
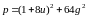 ,
то есть
,
то есть
 и
и
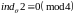 ,
где
,
где
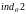 - дискретный логарифм 2 по основанию
по модулю
;
- дискретный логарифм 2 по основанию
по модулю
;
2.
![]() ,
где
,
где
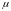 –
корень уравнения
–
корень уравнения
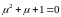 ,
если
,
если
 ,
то есть
и
,
то есть
и
 ;
;
3.
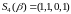 или
или
 ,
если
,
если
![]() ,
то есть
,
то есть
 и
;
и
;
4.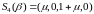 ,
если
,
если
 ,
то есть
и
;
,
то есть
и
;
5.  или
или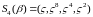 ,
если
,
если
 ,
где
,
где
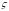 - корень пятнадцатой степени из единицы
в расширении поля
,
при этом он удовлетворяют уравнению
- корень пятнадцатой степени из единицы
в расширении поля
,
при этом он удовлетворяют уравнению
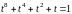 .
В первом варианте
.
В первом варианте
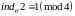 ,
а во втором
,
а во втором
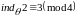 .
Отметим, что
.
Отметим, что
 будет корнем 3 из единицы, поэтому можно
считать без нарушения общности, что
будет корнем 3 из единицы, поэтому можно
считать без нарушения общности, что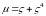 .
.
Далее, так как
справедливо разложение
 ,
то для
,
то для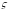 возможны
два варианта:
возможны
два варианта:
1. - корень первого множителя, тогда является корнем пятой степени из единицы;
2. -корень второго множителя, тогда он первообразный корень пятнадцатой степени из 1.
Для удобства
вычислений обозначим через
именно корень пятнадцатой степени из
единицы и, в первом случае заменим ς
на .
Таким образом, мы имеем 4 варианта:
.
Таким образом, мы имеем 4 варианта:
5a. ,
здесь
;
,
здесь
;
5b.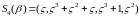 ,
здесь
,
здесь
 ;
;
5c.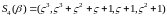 ,
здесь
;
,
здесь
;
5d.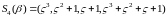 ,
здесь
.
,
здесь
.
При этом выполняются
соотношения: ,
,
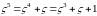 ,
,
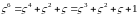 и так далее.
и так далее.
Формулы для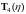 аналогичны.
аналогичны.
Сразу же заметим,
что в первых четырех вариантах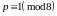 ,
то есть
,
то есть
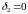 ,
а в пятом
,
а в пятом
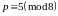 ,
тогда
,
тогда
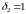 .
Аналогично, если для q
имеет место
один из первых четырех вариантов, то
.
Аналогично, если для q
имеет место
один из первых четырех вариантов, то
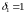 ,
а в пятом -
,
а в пятом -
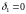 .
.
Приведем несколько значений простых чисел, удовлетворяющих условиям каждого из вариантов:
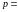 13,
353,593;
13,
353,593;17, 929;
73, 89, 233;
41, 313, 761;
5,13, 61;
5a) 13, 29,61;
5b) 397,1069;
5c) 5, 37, 53;
5d) 277, 1093.
Введем дополнительно
следующие обозначения. Пусть
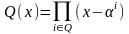 ,
,
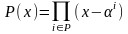 и
и
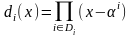 .
.
Для получения быстрых и точных расчетов простых чисел была использована следующая программа:

Рисунок 1.Пример
расчета простых чисел для![]() .
.

Рисунок 2. Пример расчета простых чисел для .
Для получения
значений
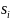 была использована программа Mathcad.
С помощью неё были рассчитаны матрицы
H:
была использована программа Mathcad.
С помощью неё были рассчитаны матрицы
H:

Рисунок 3. Пример расчета матрицы Н в программе Mathcad.
Лемма 2.3. Если
последовательность X
задана правилом (2.1) и
, ,то
,то
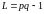 и
и
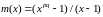 .
.
Доказательство.
Согласно
приложению ,
а по условию леммы
и
,
тогда согласно формуле (2.3)
,
а по формуле
.
,
а по условию леммы
и
,
тогда согласно формуле (2.3)
,
а по формуле
.
Таблица 1 — Численные примеры для леммы 2.3.
p |
Q |
N |
L |
p |
Q |
N |
L |
17 |
13 |
221 |
220 |
17 |
29 |
493 |
492 |
41 |
13 |
533 |
532 |
41 |
29 |
1189 |
1188 |
73 |
61 |
4453 |
4452 |
73 |
13 |
949 |
948 |
89 |
61 |
5429 |
5428 |
89 |
29 |
2581 |
2580 |
Лемма 2.4. Если
последовательность X
задана правилом (2.1) и

 то
то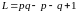 и
и
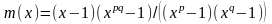 .
.
Доказательство.
Согласно
приложению
,
а по условию леммы и
,
тогда согласно формуле (2.3)
и
и
,
тогда согласно формуле (2.3)
и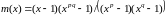 .
.
Таблица 2 — Численные примеры для леммы 2.4.
p |
Q |
N |
L |
p |
q |
N |
L |
5 |
17 |
85 |
64 |
5 |
41 |
205 |
160 |
13 |
17 |
221 |
192 |
13 |
73 |
949 |
864 |
29 |
73 |
2117 |
2016 |
29 |
17 |
493 |
448 |
61 |
41 |
2501 |
2400 |
61 |
17 |
1037 |
960 |
Аналогично предыдущим леммам получаются следующие утверждения:
Лемма 2.5. Если последовательность X задана правилом (2.1), то:
1)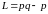 для
для
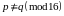 и
и
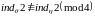 ;
;
2) для
для
 и
и
 ;
;
3)
 для
и
;
для
и
;
4)
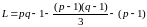 для
для
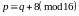 и
;
и
;
Таблица 3 — Численные примеры для леммы 2.5.
Вариант |
p |
q |
N |
L |
1 |
17 |
73 |
1241 |
1224 |
|
113 |
41 |
2993 |
1512 |
2 |
113 |
353 |
39889 |
29920 |
|
17 |
929 |
12064 |
15793 |
|
73 |
89 |
4840 |
6497 |
|
41 |
313 |
12833 |
9672 |
3 |
17 |
113 |
1921 |
1008 |
|
41 |
73 |
2993 |
1512 |
|
41 |
89 |
3649 |
1848 |
|
17 |
353 |
6001 |
3168 |
4 |
73 |
113 |
8249 |
2128 |
|
17 |
41 |
697 |
200 |
|
313 |
17 |
5321 |
1264 |
|
89 |
113 |
10057 |
2576 |
Лемма 2.6. Если последовательность X задана правилом (2.1), то:
1).
Если
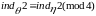 ,
то
,
то
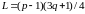 ,
если
,
если
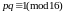 (A)
и
(A)
и
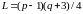 (B),
если
(B),
если
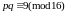 ;
;
2).
Если
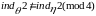 ,
то
,
то
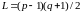 (C),
если
и
(C),
если
и
 (D),
если
.
(D),
если
.
Таблица 3 — Численные примеры для леммы 2.6.
Вариант |
p |
q |
N |
L |
A |
13 |
5 |
65 |
48 |
|
397 |
277 |
109969 |
82368 |
B |
13 |
29 |
377 |
96 |
|
397 |
1069 |
424393 |
106128 |
|
5 |
37 |
185 |
40 |
|
277 |
1093 |
302761 |
75624 |
C |
13 |
277 |
3601 |
1668 |
|
397 |
5 |
1985 |
1188 |
D |
13 |
397 |
5161 |
4764 |
|
5 |
277 |
1385 |
1108 |
ЗАКЛЮЧЕНИЕ
Линейная сложность последовательности является важной характеристикой её качества. Последовательности, обладающие высокой линейной сложностью, важны для криптографических приложений.
В выпускной
квалификационной работе исследована
линейная сложность обощенных
циклотомических последовательностей
четвертого порядка с периодом
 .
Определено, при каких значениях параметров
они обладают высокой линейной сложностью.
.
Определено, при каких значениях параметров
они обладают высокой линейной сложностью.
