
- •Министерство образования и науки Российской федерации
- •«Новгородский государственный университет имени Ярослава мудрого»
- •Содержание
- •Перечень сокращений, символов и специальных терминов
- •Введение
- •Обобщеные циклотомические оследовательности
- •Основные опрЕделения
- •1.3 Обобщенные циклотомические классы по модулю
- •Вычисление линейной сложности последовательностей четвертого порядка
- •Список использованной литературы
1.3 Обобщенные циклотомические классы по модулю
Пусть

![]() – простое число, где
– простое число, где
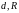
![]() –
натуральные числа. Обозначим через
–
натуральные числа. Обозначим через
 –
класс вычетов степени
–
класс вычетов степени
 по
модулю
,
то есть
по
модулю
,
то есть
 ,
здесь
,
здесь
 – первообразный корень по модулю
– первообразный корень по модулю
![]() [1],
[1],
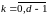 .
Положим
.
Положим
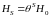
![]() ,
где
,
где ![]()
 (все действия выполняются по модулю
),
тогда
(все действия выполняются по модулю
),
тогда
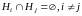 и порядок
и порядок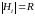 .
.
Согласно [2],
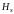 -
являются циклотомическими классами и
-
являются циклотомическими классами и
 .
(1.3.1)
.
(1.3.1)
Пусть
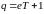 – простое число, где
– простое число, где
 – натуральные числа и
– натуральные числа и
 ,
,
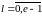 ,
где
,
где
 – первообразный корень по модулю
– первообразный корень по модулю
 ,
тогда порядок
,
тогда порядок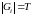 и
и
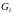 -
циклотомические классы. Как и ранее
-
циклотомические классы. Как и ранее
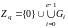 . (1.3.2)
. (1.3.2)
Обозначим
через
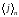
![]() –
наименьший неотрицательный вычет целого
числа
–
наименьший неотрицательный вычет целого
числа ![]()
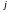 по модулю
по модулю ![]()
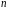 .
.
Рассмотрим классы
вычетов по модулю N,
построенные следующим образом:
 ,
,
 .
Следовательно, каждый класс
.
Следовательно, каждый класс
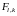 содержит
содержит
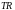 чисел и, если
чисел и, если
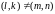 ,
то пересечение
с
,
то пересечение
с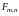 пусто [1]. Из определения следует, что
пусто [1]. Из определения следует, что
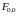 является подгруппой мультипликативной
группы
является подгруппой мультипликативной
группы
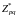 .
.
Согласно китайской
теореме об остатках, кольцо классов
вычетов 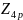
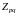
 изоморфно прямому произведению
изоморфно прямому произведению

 .
Пусть
.
Пусть
 -
соответствующий изоморфизм, то есть
-
соответствующий изоморфизм, то есть
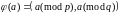 ,
тогда
,
тогда
 при
при
 ,
и, если
,
и, если
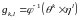 ,
то
,
то
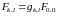 .
Таким образом,
.
Таким образом,
 являются циклотомическими классами и
являются циклотомическими классами и
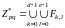 .
(1.3.3)
.
(1.3.3)
Добавим еще три
вида классов вычетов: ,
,
 ,
тогда порядок
,
тогда порядок
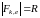 при
при и
и
 при
при
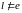 .
Соответственно,
.
Соответственно,
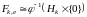 при
и
при
и
 ,
при
и
,
при
и
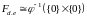 .
Из формул (1.3.1,1.2.,1.3.3) имеем
.
Из формул (1.3.1,1.2.,1.3.3) имеем
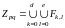 .
(1.3.4)
.
(1.3.4)
Отметим, что
согласно определению ,
,
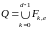 .
Также, далее, для удобства записи будем
отождествлять изоморфные множества
.
Также, далее, для удобства записи будем
отождествлять изоморфные множества
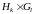 и
и
 .
.
Рассмотрим
примеры разбиения на классы вычетов
для различных значений
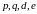 .
.
Пример 1.
Пусть
 ,
,
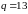 ,
,
 ,
,
 ,
,
 ,
,
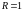 ,
,
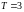 .
.
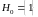 ,
,
 ,
,
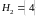 ,
,
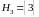 .
.
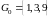 ,
,
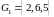 ,
,
 ,
,
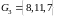 .
.
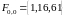 ,
,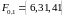 ,
, ,
, .
.
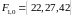 ,
,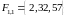 ,
,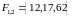 ,
,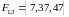 .
.
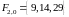 ,
,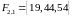 ,
,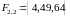 ,
,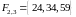 .
.
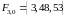 ,
,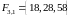 ,
, ,
, .
.
 ,
,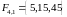 ,
,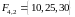 ,
,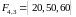 .
.
 ,
,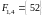 ,
, ,
,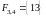 .
.
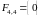 .
.
В [7] было показано, что имеет место следующее утверждение.
Лемма 1.1.
Если
и
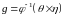 ,
то справедливо равенство:
,
то справедливо равенство:
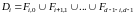 ,
.
(1.3.5)
,
.
(1.3.5)
Пример 4.
Пусть, как и в примере 3 , , , , тогда
 ,
,
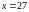 .
После вычислений, получаем:
.
После вычислений, получаем:
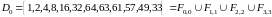 ,
,
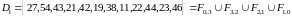 ,
,
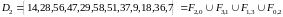 ,
,
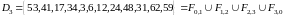 .
.
Таким образом, для
расчета линейной сложности
последовательностей можно использовать
метод, предложенный в [7]. Он заключается
в вычислении значений многочлена на
представителях классов
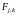 .
Напомним, кратко его основные положения.
.
Напомним, кратко его основные положения.
1.4 ЦИКЛОТОМИЧЕСКИЕ ЧИСЛА И ЛИНЕЙНАЯ СЛОЖНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТЕЙ, СФОРМИРОВАННЫХ НА ОСНОВЕ КЛАССОВ СТЕПЕННЫХ ВЫЧЕТОВ
Определение.
Последовательность
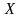 удовлетворяющая соотношению
удовлетворяющая соотношению
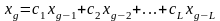 (1.4.1)
(1.4.1)
для
всех
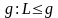 ,
,
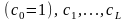 из
называется линейной рекуррентной
последовательностью.
из
называется линейной рекуррентной
последовательностью.
Наименьшее
значение
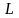 ,
для которого выполняется соотношение
(1.4.1) называется линейной сложностью
(эквивалентной линейной сложностью,
рангом) последовательности над полем
.
,
для которого выполняется соотношение
(1.4.1) называется линейной сложностью
(эквивалентной линейной сложностью,
рангом) последовательности над полем
.
Линейные рекуррентные последовательности можно получить с помощью регистра сдвига с обратной связью. Поэтому, линейную сложность последовательности также определяют как длину самого короткого линейного регистра сдвига с обратными связями, который может воспроизвести последовательность.
Многочлен
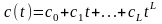 – называют минимальным или характеристическим
многочленом последовательности
– называют минимальным или характеристическим
многочленом последовательности
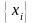 .
.
В этом подразделе рассмотрим метод расчета линейной сложности двоичных последовательностей, сформированных на основе классов степенных вычетов, основанный на применении циклотомических чисел. Известные методы расчета линейной сложности ДКП, сформированных на основе классов степенных вычетов, тесно связаны с применяемым правилом кодирования.
Как и ранее, пусть
ДП X
с периодом
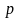 сформирована по обобщенному ПК:
сформирована по обобщенному ПК:
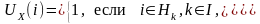 (1.4.2)
(1.4.2)
Согласно
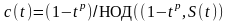 ,
(1.4.3)
,
(1.4.3)
где
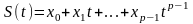 ,
более того:
,
более того:
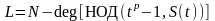 .
(1.4.4)
.
(1.4.4)
Если рассмотреть
разложение многочлена
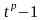 на неприводимые множители над
,
то всегда можно построить конечное
поле, которое содержит все его корни.
Такое поле называется полем разложения
многочлена
.
на неприводимые множители над
,
то всегда можно построить конечное
поле, которое содержит все его корни.
Такое поле называется полем разложения
многочлена
.
Пример 1. Пусть
 ,
тогда, несложно убедиться, что
,
тогда, несложно убедиться, что
 и
многочлены
и
многочлены
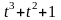 ,
,
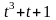 - неприводимы над
.
В этом случае, элементы мультипликативной
группы конечного поля
- неприводимы над
.
В этом случае, элементы мультипликативной
группы конечного поля
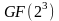 ,
построенного по многочлену
или
будут корнями 7 степени из единицы.
,
построенного по многочлену
или
будут корнями 7 степени из единицы.
Пусть
 – примитивный корень степени
из единицы в поле разложения
– примитивный корень степени
из единицы в поле разложения
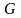 многочлена
над
.
Тогда, согласно формуле (1.4.4), для ДП
(БП):
многочлена
над
.
Тогда, согласно формуле (1.4.4), для ДП
(БП):
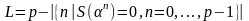 .
(1.4.5)
.
(1.4.5)
Таким образом,
вычисление линейной сложности
последовательности
 сводится к
вычислению корней многочлена
сводится к
вычислению корней многочлена
 в множестве:
в множестве:
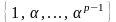 .
.
Введем дополнительный
многочлен
 .
.
Следующая лемма
описывает свойства многочлена
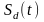 ,
она доказана в [20].
,
она доказана в [20].
Лемма 1.2.
Если
 ,
то в поле
справедливы следующие соотношения:
,
то в поле
справедливы следующие соотношения:
1)
 для
для
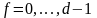 .
.
2)
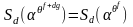 для любого
целого числа
.
для любого
целого числа
.
3) Если
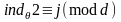 ,
то
,
то
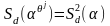 .
.
Пример 1.
Пусть
,
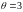 ,
,
 ,
тогда
,
тогда
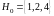 ,
,
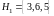 .
По определению
.
По определению
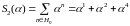 ,
далее
,
далее
 ,
следовательно,
,
следовательно,
 .
.
Отметим ещё одно
свойство многочлена
.
Из равенства
 следует, что в поле
сумма
следует, что в поле
сумма
 ,
т. е.
,
т. е.
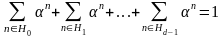 и, по лемме 1.4.1 имеем
и, по лемме 1.4.1 имеем
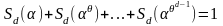 .
(1.4.6)
.
(1.4.6)
Например, если
,
то
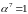 или
или
 .
Тогда
,
.
Тогда
,
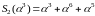 и
и
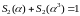 .
.
Далее, не нарушая
общности, можно считать, что
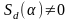 .
В противном случае, выбираем другой
первообразный корень из единицы.
.
В противном случае, выбираем другой
первообразный корень из единицы.
По определению
последовательности получаем, что
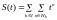 ,
тогда
,
тогда
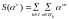 или, по лемме 1.2 ,
или, по лемме 1.2 ,
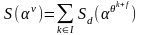 ,
если
,
если
 .
Таким образом, для нахождения корней
многочлена
достаточно определить значения
.
Таким образом, для нахождения корней
многочлена
достаточно определить значения
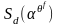 ,
.
Более того, значения
,
.
Более того, значения
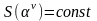 ,
если
и из (4.6.4) получаем, что линейная сложность
ДП
,
если
и из (4.6.4) получаем, что линейная сложность
ДП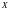 равна
равна
 .
(1.4.7)
.
(1.4.7)
Теорема 1.1.
Если
 ,
то
,
то

где
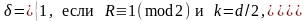
Теорема 1.1. определяет
систему уравнений для неизвестных
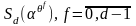 с использованием таблицы циклотомических
чисел порядка
.
Её решение позволяет определить значения
с использованием таблицы циклотомических
чисел порядка
.
Её решение позволяет определить значения
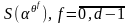 Последнее, согласно соотношению (1.4.7),
делает возможным расчет линейной
сложности рассматриваемых ДП.
Последнее, согласно соотношению (1.4.7),
делает возможным расчет линейной
сложности рассматриваемых ДП.
1.5 МЕТОД ВЫЧИСЛЕНИЯ ЛИНЕЙНОЙ СЛОЖНОСТИ ЦИКЛОТОМИЧЕСКИХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Линейная
составляющая последовательности
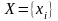 с периодом
с периодом
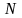 по конечной области
по конечной области
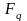 ,
где
,
где
 является простым числом, определяется
как минимальное положительное целое
число
,
для которого существуют константы
является простым числом, определяется
как минимальное положительное целое
число
,
для которого существуют константы
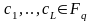 такой, что
такой, что
 for
all
for
all
 [1].
[1].
Полином-многочлен
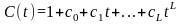 называется минимальным из последовательности
в
котором
называется минимальным из последовательности
в
котором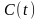 следует [1]
следует [1]
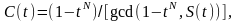 (1.5.1)
(1.5.1)
где
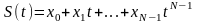 является полином-многочленом
последовательности. Тогда по (1) мы имеем
является полином-многочленом
последовательности. Тогда по (1) мы имеем
 (1.5.2)
(1.5.2)
Пусть
простое,
единственный корень в области
полином-многочлена
 в областий
и
в областий
и .
Из (1.5.2) из этого следует
.
Из (1.5.2) из этого следует
 (1.5.3)
(1.5.3)
Таким
образом, проблема о вычислении линейной
сложности последовательности
уменьшен до определенного значения
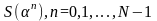 в области
в области
 .
Те же самые условия позволяют вычислять
минимальный полином-многочлен
последовательности, согласно (1.5.1), мы
имеем
.
Те же самые условия позволяют вычислять
минимальный полином-многочлен
последовательности, согласно (1.5.1), мы
имеем
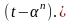 (1.5.4)
(1.5.4)
В
этом разделе мы исследуем метод вычисления
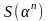 для циклотомических последовательностей
периодом.
для циклотомических последовательностей
периодом.
Пусть
 нечетное, где
нечетное, где
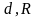 являются натуральными числами,
являются натуральными числами,
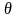 является простым модулем корня
и
является простым модулем корня
и
 ,
,
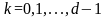 являются циклотомическими классами
значений
[9].
являются циклотомическими классами
значений
[9].
Давайте рассматривать последовательность с периодом , построенный следующим способом:
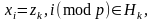 (1.5.5)
(1.5.5)
где
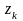 - предопределенные числа в области
.
Давайте предполагать значения
- предопределенные числа в области
.
Давайте предполагать значения
 ,
если переменная не предусмотрена.
,
если переменная не предусмотрена.
Тогда,
мы вводим вспомогательный полином-многочлен
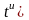 .
.
Следующая
лемма - простое обобщение утверждений,
доказанных в [3,4] для
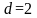 и
и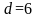 .
.
Лемма
1.3.
Если
 ,
тогда
,
тогда
 ;
;
если
f
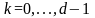 ,
тогда
,
тогда
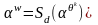 .
.
От леммы 1.3 мы периходим
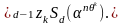 (1.5.6)
(1.5.6)
Таким
образом, чтобы вычислить значения
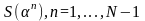 достаточно найти
достаточно найти
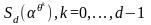 .Что
позволит нам ввести примечание
.Что
позволит нам ввести примечание
 .
Метод вычисления
.
Метод вычисления
 составляет основное содержание раздела.
составляет основное содержание раздела.
Сначала,
мы отмечаем
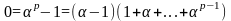 ,
поэтому по лемме 1.3, мы имеем
,
поэтому по лемме 1.3, мы имеем
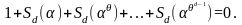 (1.5.7)
(1.5.7)
В частности одна из лемм вспомогательного полином-многочлена всегда отличается от ноля. Не нарушая заурядность мы можем предположить, что .
Мы
напоминаем что циклотомическое число
 порядка
является множеством решений соответствия
порядка
является множеством решений соответствия
 [10]. Следующая лемма вытекает из
определения циклотомических чисел.
[10]. Следующая лемма вытекает из
определения циклотомических чисел.
Лемма
1.4.
Если
 тогда
число решений соответствия
тогда
число решений соответствия
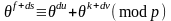 когда
когда
 равняется
.
равняется
.
Тогда докажемм основную теорему раздела.
Теорема
1.2.
Для
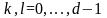 мы имеем
мы имеем

где
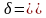
Докозательство.
По определению
и
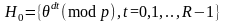 ,
Поэтому
,
Поэтому
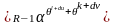 .
If
.
If
 ,
тогда
является простым корнем, из числа
,
тогда
является простым корнем, из числа
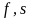 так как
так как
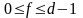 ,
,
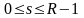 и
и или
или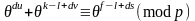 .
По лемме 2, за каждое значение
.
По лемме 2, за каждое значение
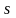 число пар
число пар
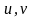 ,
будучи решениями последнего соответствия,
совпадает с циклотомическим числом
,
будучи решениями последнего соответствия,
совпадает с циклотомическим числом
 .
так, что
.
так, что
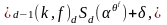
где
 является множеством решений:
является множеством решений:
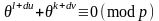 .
По этому
.
По этому
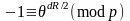 ,
тогда
как в теореме, которая была доказана.
,
тогда
как в теореме, которая была доказана.
вычислить линейную сложность последовательности, в зависимости от модуля отстатка и его представления в форме суммы площадей чисел целого числа. Следствия следующих разделов подтвердят последнее утверждение.
1.6 О ЛИНЕЙНОЙ СЛОЖНОСТИ ДВОЙНЫХ И ТРОИЧНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ, ПОСТОЯННЫХ НА ВТОРЫХ-ВОСЬМЫХ ПОРЯДКОВ ЦИКЛОТОМИЧЕСКИХ ЧИСЕЛ
В
этом разделе мы иллюстрируем изложенные
выше методы с примерами вычисления
линейной сложности двойных и троичных
последовательностей по областям
где .
.
1.6.1.
Пусть
и
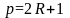 .
Используем теоремму 1 когда
.
Используем теоремму 1 когда
 ,
тогда
,
тогда
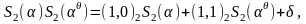 (1.6.1)
(1.6.1)
где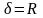 ,
если
является нечетным и нулевым. По формуле
(7) мы имеем
,
если
является нечетным и нулевым. По формуле
(7) мы имеем
 (1.6.2)
(1.6.2)
Циклотомические
числа второго порядка зависящие от
,
если
четно, тогда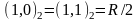 ,
и если
является нечетным, тогда
,
и если
является нечетным, тогда
 .
Поэтому, по (1.6.1) и (1.6.2) формуле мы получаем,
что
.
Поэтому, по (1.6.1) и (1.6.2) формуле мы получаем,
что Следовательно,
Следовательно,
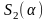 и
и
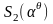 являются корнями полином-многочлена
являются корнями полином-многочлена
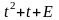 .
Принятие во внимание предположения
.
Принятие во внимание предположения
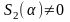 ,
мы получаем
,
мы получаем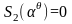 тогда и только тогла
тогда и только тогла
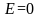 в области
.
в области
.
если
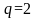 ,
тогда
для
,
тогда
для
 или
или
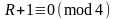 ,
поэтому:
,
поэтому:
1).
 ,
если
,
если
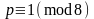 или
или
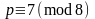 ;
;
2).
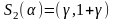 ,
где является корнем уравнения
,
где является корнем уравнения
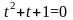 ,
если
,
если
 или
или
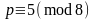 .
.
В
случае, если
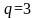 ,
тогда
для
,
тогда
для
 или
или
 ,
так:
,
так:
1).
,
если или
или
 ;
;
2).
 ,
где
,
где
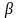 - корень уравнения
- корень уравнения
 ,
если
,
если
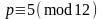 или
или
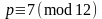 .
.
1.6.2.
Пусть
 ,
и
,
и
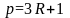 .
Циклотомические числа третьего порядка
сформированы разложением
.
Циклотомические числа третьего порядка
сформированы разложением
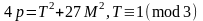 ,
где
,
где
 являются целыми числами [10]. В частности
мы имеем
являются целыми числами [10]. В частности
мы имеем
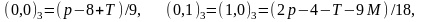
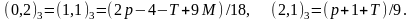
Если
и
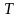 четно, тогда модуль остатков два из
перечисленных циклотомических чисел
равняется нолю, исключая
четно, тогда модуль остатков два из
перечисленных циклотомических чисел
равняется нолю, исключая
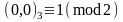 .
По теореме 1.3 и формуле (1.5.7), мы получаем
следующий набор уравнения для неизвестного
.
По теореме 1.3 и формуле (1.5.7), мы получаем
следующий набор уравнения для неизвестного
 ,
,
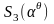 и
и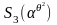 :
:
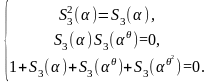 (1.6.3)
(1.6.3)
По
формуле (1.6.3) , мы получаем
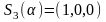 ,
если
,
если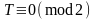 .
.
В
случае, если
 ,
тогда
,
тогда
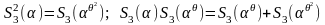 для
для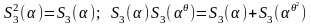 .
Тогда
.
Тогда
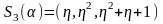 ,
где
,
где
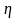 - корень уравнения
- корень уравнения
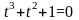 .
.
Полученные
значения
позволяют вычислять линейную сложность
последовательностей, например если
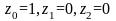 ,
то есть, (1.5.6),
является характерной последовательностью
,
то есть, (1.5.6),
является характерной последовательностью
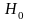 ,
где
,
где
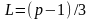 для
для
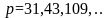 и
и
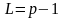 когда
когда
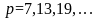 .
.
В
случае, если
,
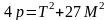 и
is
even,
тогда
и
is
even,
тогда
 и
и
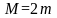 .
В таких остатках выбора циклотомических
чисел третьего порядка, вычислены
формулами:
.
В таких остатках выбора циклотомических
чисел третьего порядка, вычислены
формулами:
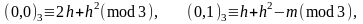

Тогда, для теореме 1.2 и формуле (1.5.7) мы получаем следующую систему уравнений:
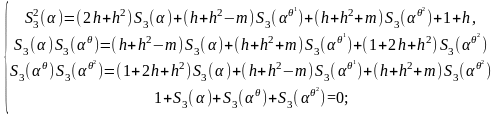 (1.6.4)
(1.6.4)
Исследование
(1.6.4), и также подобронного к нему значения
,
зависящие от остатков
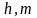 ,
и значений
мы получаем следующие решения:
,
и значений
мы получаем следующие решения:
1).
 (до перестановки), если
(до перестановки), если
 ,
,
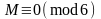 или
или
 ,
,
 ;
;
2).
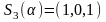 ,
,
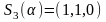 ,
если
,
если
 ,
или
,
или
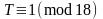 ,
;
,
;
3).
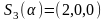 ,
если
,
если
 ,
или
,
или
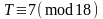 ,
;
,
;
4).
 ,
где
,
где
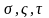 являются корнями уравнения:
являются корнями уравнения:
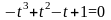 ,
если
,
,
если
,
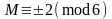 или
,
или
,
 ;
;
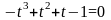 ,
если
,
или
,
;
,
если
,
или
,
;
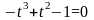 ,
если
,
или
,
.
,
если
,
или
,
.
Циклотомические
изменения значений
не влияют на вычисление линейной
сложности. Кроме того,
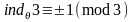 ,
если
,
если
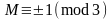 [10], тогда
[10], тогда
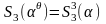 .
По этому,
.
По этому,
 ,
по (7) - корни полином-многочлена
,
по (7) - корни полином-многочлена
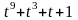 ,
который разложен на множители в области
,
который разложен на множители в области
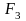 следующим образом
следующим образом
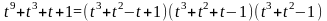 .
Это точно соответствует результатам
последнего, четвертого случая.
.
Это точно соответствует результатам
последнего, четвертого случая.
1.6.3.
Пусть
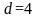 ,
для
,
для
 .
В этом подразделе и в следующих мы
ограничимся с исследованием значений
полином-многочлена двоичной
последовательности, потому что линейная
сложность троичных последовательностей
когда
.
В этом подразделе и в следующих мы
ограничимся с исследованием значений
полином-многочлена двоичной
последовательности, потому что линейная
сложность троичных последовательностей
когда
 в области
был изучен в [11]. Циклотомические числа
четвертого порядка сформированы
разложением:
в области
был изучен в [11]. Циклотомические числа
четвертого порядка сформированы
разложением:
 [10], где
[10], где
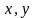 - целые числа, и зависят от
,
совпадает с
- целые числа, и зависят от
,
совпадает с
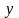 .
.
Если
даже является следствиями подраздела
1.6.1,
.
По определению вспомогательного
полином-многочлена,
 ,
где
,
где
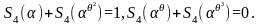 (1.6.5)
(1.6.5)
Для циклотомические числа четвертого порядка, сформированны
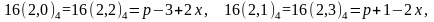
После
вычисления их модуля два остатка
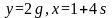 ,
где
,
где
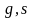 являются целыми числами, по теореме 1.2
и формуле (1.6.5), мы имеем
являются целыми числами, по теореме 1.2
и формуле (1.6.5), мы имеем
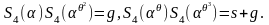 (1.6.6)
(1.6.6)
После изучения (1.6.5) и (1.6.6), в зависимости от модуля остатков мы получаем:
1).
 , если
, если
 ,
,
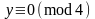 ;
;
2).
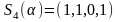 , если
, если
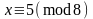 ,
;
,
;
3).
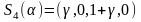 , если
,
, если
,
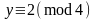 ,
где
,
где
 является корнем уравнения:
;
является корнем уравнения:
;
4).
 , если
,
.
, если
,
.
Если - нечетный, тогда как и показанно в разделе 1.6.1, . В этом случае, то же самое что касается значения .
5).
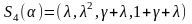 , если
, если
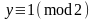 ,
где
,
где
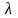 является корнем уравнения:
является корнем уравнения:
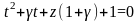 or
or
 ,
где
,
где
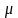 является корнем уравнения
является корнем уравнения
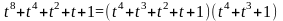 .
Если
.
Если
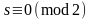 ,
где
является корнем первого порядка, иначе
второго. Полученные формулы для
,
где
является корнем первого порядка, иначе
второго. Полученные формулы для
 позволят вычислять линейную сложность
и минимальный полином-многочлен любой
двоичной последовательности простого
периода
,
построенный в циклотомических классах
четвертого порядка, включая изученные
в [5]. Особенно, если
является характерной последовательностью
биквадратного класса остатка, тогда
позволят вычислять линейную сложность
и минимальный полином-многочлен любой
двоичной последовательности простого
периода
,
построенный в циклотомических классах
четвертого порядка, включая изученные
в [5]. Особенно, если
является характерной последовательностью
биквадратного класса остатка, тогда
 ,
если
,
если
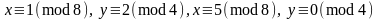 или
.
или
.
1.6.4.
Пусть
,
для
 .
Циклотомические числа 6 порядка
сформированы разложением:
.
Циклотомические числа 6 порядка
сформированы разложением:
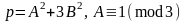 [12], где
[12], где
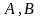 являются целыми числами, в зависимости
от
.
являются целыми числами, в зависимости
от
.
По
определению вспомогательного
полином-многочлена мы имеем
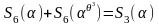 .
Которые показывают в подразделе 1.6.2
значения
завищащие от
,
где
определена от разложения
.
От отношений между
и
[10] мы получаем это, тогда и только тогда,
когда
.
Которые показывают в подразделе 1.6.2
значения
завищащие от
,
где
определена от разложения
.
От отношений между
и
[10] мы получаем это, тогда и только тогда,
когда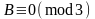 .
Следовательно, если
,
когда
и
.
Следовательно, если
,
когда
и
 (1.6.7)
(1.6.7)
Если
является нечетным, тогда
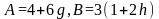 и циклотомические числа шестого порядка
определены [12]:
и циклотомические числа шестого порядка
определены [12]:
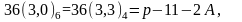
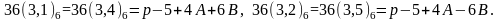
После вычисления их по модулю два по теореме 1.1, мы добираемся
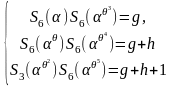 (1.6.8)
(1.6.8)
Решение (1.6.7) и (1.6.8) приводит к следующему:
1).
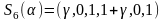 , если
, если
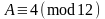 ,
,
 ,
где
i
корень уравнения:
;
,
где
i
корень уравнения:
;
2).
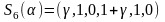 , если
,
, если
,
 ;
;
3). , если
, если
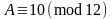 ,
;
,
;
4).
 , если
,
.
, если
,
.
Полученные
значения
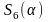 с данными предположениями, позволят
вычислить линейную сложность любой
двоичной последовательности, постоянной
на циклотомических числах шестого
порядка, включая последовательности
[4]. Случаи, когда
четно,
с данными предположениями, позволят
вычислить линейную сложность любой
двоичной последовательности, постоянной
на циклотомических числах шестого
порядка, включая последовательности
[4]. Случаи, когда
четно,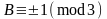 изучены таким же образом.
изучены таким же образом.
1.6.5.
Пусть
 ,
для
,
для
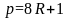 .
Циклотомические числа восьмого порядка
определены разложением
.
Циклотомические числа восьмого порядка
определены разложением
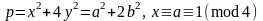 [10, 13] , где
[10, 13] , где
 являются целыми числами, и зависят от
остатка
по модулю четыре. В этом подразделе мы
ограничимся исследованием значений
являются целыми числами, и зависят от
остатка
по модулю четыре. В этом подразделе мы
ограничимся исследованием значений
 только для двоичных последовательностей
с нечетными значениями
и
.
только для двоичных последовательностей
с нечетными значениями
и
.
Как для результатов подраздела 1.6.3 мы имеем
 (1.6.9)
(1.6.9)
Если
является нечетным и
,
тогда от разложения
мы получаем
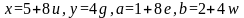 ,
где
,
где
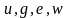 являются целыми числами. После вычисления
модуля двух остатков циклотомических
чисел восьмого порядка
являются целыми числами. После вычисления
модуля двух остатков циклотомических
чисел восьмого порядка
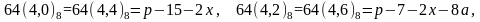
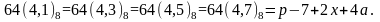
По теореме 1.1 и формуле (1.6.9) мы добираемся
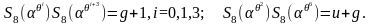 (1.6.10)
(1.6.10)
Так,
по (1.6.9) и (1.6.10) следуя за этим, числа
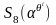 принадлежат множеству
принадлежат множеству
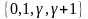 ,
где корень полином-многочлена
,
где корень полином-многочлена
 ,
и зависят от остатков
,
и зависят от остатков
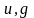 по модулю два. Чтобы упорядочить их, мы
используем заключение теоремы 1.1. В
данном случае
по модулю два. Чтобы упорядочить их, мы
используем заключение теоремы 1.1. В
данном случае
 Наконец мы получаем:
Наконец мы получаем:
1).
 , или
, или
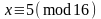 ,
,
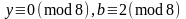 ;
;
2).
 , или
,
, или
,
 ;
;
3).
 , или
, или
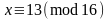 ,
;
,
;
4).
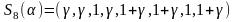 , или
,
;
, или
,
;
5).
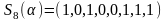 , или
,
, или
,
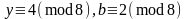 ;
;
6).
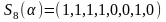 , или
,
, или
,
 ;
;
7).
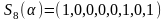 , или
,
;
, или
,
;
8).
 , или
,
.
, или
,
.
Лемма
1.5.
Если
является характерной последовательностью
набора различных остатков, тогда его
линейная сложность равняется
 ,
и в случае, если, когда
соответствует
набору разных остатков и ноля, тогда
,
и в случае, если, когда
соответствует
набору разных остатков и ноля, тогда
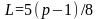 .
.
Док.
Класс остатков
в различных положониях, если
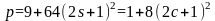 [10]. Поэтому,
[10]. Поэтому,
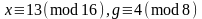 ,
тогда среди значений
есть
пять нолей. По лемме 1.5,
,
тогда среди значений
есть
пять нолей. По лемме 1.5,
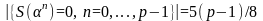 и формуле (1.5.3) следует доказательство
первого утверждения леммы 1.4. Второе мы
доказываем почти таким же способом.
Минимальный полином-многочлен
последовательности
может быть вычислен в случае (1.5.4).
и формуле (1.5.3) следует доказательство
первого утверждения леммы 1.4. Второе мы
доказываем почти таким же способом.
Минимальный полином-многочлен
последовательности
может быть вычислен в случае (1.5.4).
1.7
ПРИМЕРЫ ВЫЧИСЛЕНИЯ ЛИНЕЙНОЙ СЛОЖНОСТИ
ДВОИЧНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ С ПЕРИОДАМИ
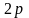 И
И
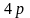
В этом разделе мы
будем демонстрировать что полученные
более ранние результаты относительно
значений
позволит нам в некоторых случаях выбрать
двоичные последовательности с периодом
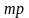 , где
, где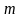 имеет сложную линейную сложность.
имеет сложную линейную сложность.
Согласно китайской
Теореме Остатка, кольца остатков
 является изоморфным к прямому продукту
является изоморфным к прямому продукту
 [9]. Пусть
[9]. Пусть
 ,
где
,
где
 ,
,
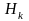 как прежде, циклотомические классы
порядка
,
как прежде, циклотомические классы
порядка
,
 является подмножеством индексов
является подмножеством индексов
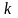 .
.
Исследуем двоичную последовательность , определенную как
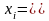 (1.6.11)
(1.6.11)
Для последовательности формула (1.5.2) будет похожа
 (1.6.12)
(1.6.12)
Следовательно, в
этом случае , вычисление линейной
сложности уменьшено до определения
общих корней полином-многочленов
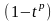 и
,
приводит к исследованию значений
и
,
приводит к исследованию значений
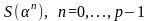 .
.
Лемма 1.6.
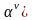 .
.
Докозательство.
Для
 ,
когда
,
когда
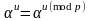 .
Когда
.
Когда
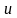 принимает значения от
принимает значения от
 ,
тогда остаток
,
тогда остаток
 принимает значения
от
,
которые должны были быть доказан в
лемме.
принимает значения
от
,
которые должны были быть доказан в
лемме.
Следующая лемма следует из лемм 1.5 и 1.6.
Лемма 1.7. Если полином-многочлен последовательности , т
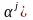
Лемма 1.6 показывает, значения полином-многочлена последовательности которая может быть найдена, в результате уже известных значений .
Лемма 1.8.
Если двоичная последовательность
определенна в (1.6.11)
для подмножества
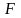 равная
равная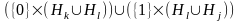 ,
где
-циклотомические
классы четвертого порядка,
,
где
-циклотомические
классы четвертого порядка,
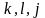 - различных индексов от ноля до трех,
тогда его линейная сложность
- различных индексов от ноля до трех,
тогда его линейная сложность
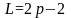 ,
if
,
if
 или
и
или
и
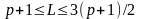 ,
если
или
,
если
или .
.
Докозательство.
По лемме 1.4,
 .
Извлекая пользу из значений
найденные в подразделе 1.6.4, после
подведения итогов мы получаем
.
Извлекая пользу из значений
найденные в подразделе 1.6.4, после
подведения итогов мы получаем
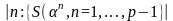 равные нолю, если
равные нолю, если
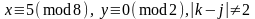 или
и равняется
или
и равняется
 .
.
Просто удостовериться
этому, когда
 значения
значения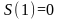 и единственность - кореня со степенью
два. По этому и формуле (1.6.12)
мы получаем утверждение леммы 1.8.
и единственность - кореня со степенью
два. По этому и формуле (1.6.12)
мы получаем утверждение леммы 1.8.
Лемма 1.9.
Если двоичная последовательность
определена циклотомическими классами
четвертого порядка и формулой (1.6.11)
когда
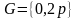 or
or
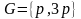 и
и
 ,
,
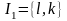 ,
,
 ,
,
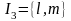 ,
тогда его линейная сложность
,
тогда его линейная сложность
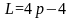 .
.
То
же самое, доказывая лемму 1.9 мы
удостоверяемся, что если утверждение
леммы 1.6 верно, то
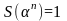 где
где
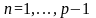 ,
и
и единственность- кореня со степенью
четыре.
,
и
и единственность- кореня со степенью
четыре.
