5 Моделирование лучших моделей
Итак, мы определили, что исходный процесс лучше всех остальных моделей приближают модели АР(3), СС(2), АРСС(3,1). Смоделируем случайную последовательность. Для этого сгенерируем выборку из 5000 отсчетов с использованием лучшей модели следующим образом:
Создадим вектор, координаты которого распределены по нормальному закону с нулевым математическим ожиданием и единичной дисперсией (белый шум).
В результирующий вектор будем записывать значения моделируемого процесса по формуле:
где
-
-ая
координата результирующего вектора
выходного процесса
- параметры модели
–
-ая
координата нормального вектора выходного
процесса
Для АР(3):
Для СС(2):
Для АРСС(3,1):
где - -ая координата результирующего вектора выходного процесса
– -ая координата нормального вектора выходного процесса.
Прибавим к полученному вектору значение выборочного среднего, найденного в пункте 1.
Результаты моделирования каждой модели представлены на рисунках 3, 4, 5:
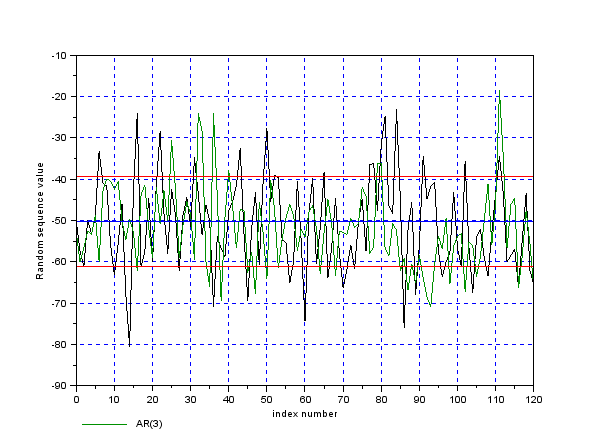
Рисунок 3 – Моделирование случайного процесса по модели АР(3)
Рисунок 4 – Моделирование случайного процесса по модели СС(2)
Рисунок 5 – Моделирование случайного процесса по модели АРСС(3,1)
Формулы для расчета теоретической корреляционной функции модели СС(2) будут выглядеть следующим образом:
Формулы для расчета теоретической корреляционной функции модели АР(3) будут выглядеть следующим образом:
Формулы для расчета теоретической корреляционной функции модели АРСС(3, 1) будут выглядеть следующим образом:
где:
Для
нормированных корреляционных функций
воспользуемся формулой:
Результаты запишем в таблицу 11.
Таблица 11 – Результаты выборочной нормированную корреляционной функции смоделированного процесса, выборочной нормированной корреляционной функции исходного процесса и теоретической нормированной корреляционной функции.
Нормированная корреляционная функция |
Исходный процесс |
АР(3) |
СС(2) |
АРСС(3,1) |
|||||
Теория |
Выборка |
Теория |
Выборка |
Теория |
Выборка |
||||
r(0) |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
||
r(1) |
0.2696 |
0.2696 |
0.2796 |
0.2696 |
0.2677 |
0.2696 |
0.2825 |
||
r(2) |
-0.1304 |
-0.1304 |
-0.1092 |
-0.1304 |
-0.1334 |
-0.1304 |
-0.0971 |
||
r(3) |
0.4014 |
0.4012 |
0.3940 |
0 |
0.0067 |
0.4014 |
0.4279 |
||
r(4) |
0.2324 |
0.3884 |
0.3668 |
0 |
0.0017 |
0.2324 |
0.2445 |
||
r(5) |
-0.1561 |
-0.0611 |
-0.0766 |
0 |
-0.0041 |
-0.1542 |
-0.1181 |
||
r(6) |
0.1046 |
0.0431 |
0.0345 |
0 |
0.0221 |
0.1086 |
0.1523 |
||
r(7) |
0.1681 |
0.2656 |
0.2566 |
0 |
0.0059 |
0.1790 |
0.1913 |
||
r(8) |
-0.0920 |
0.0681 |
0.0618 |
0 |
-0.0132 |
-0.0848 |
-0.0733 |
||
r(9) |
0.0077 |
-0.0525 |
-0.0635 |
0 |
0.0087 |
-0.0121 |
0.0125 |
||
СКО |
0.0770 |
0.0684 |
0.3039 |
0.2871 |
0.0008 |
0.0068 |
|||
Построим графики трех нормированных корреляционных функций: 1) выборочной для исходного процесса 2) теоретической для наилучшей модели 3) выборочной для смоделированного процесса и изобразим их на рисунках 6, 7 и 8.
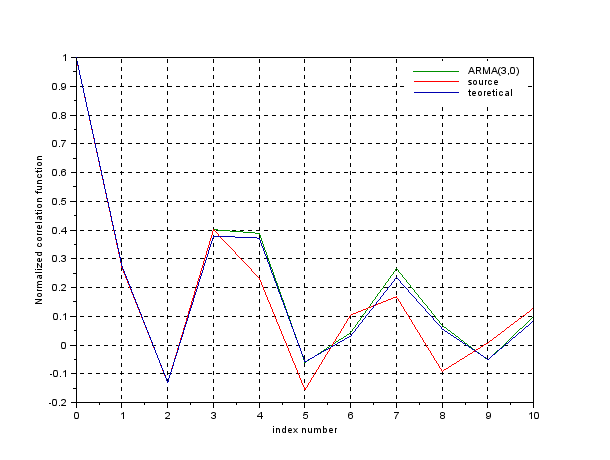
Рисунок 6 – Нормированные корреляционные функции модели АР(3)
Рисунок 7 – Нормированные корреляционные функции модели СС (2)
Рисунок 8 – Нормированные корреляционные функции модели АРСС (3,1)