2.Динамическая погрешность

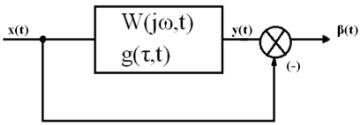W(jωt) – общая нестационарная передаточная ф-ия, g(τ,t) – импульсная. Динамическая погрешность – разность между выходными и входными величинами при отсутствии других погрешностей. β(t)=y(t)-x(t). Если есть изменяющийся во времени входной СП, то есть динамическая погрешность. Для стационарного процесса: M_β(t)= Можем показать, что на входе мат ожидание const: M_β(t)=0, так, если x(t) является const или медленно меняется с ф-ей, то мат ожидание: M[x(t)]=x(t), M[y(t)]=x(t), тогда: M[β]=M[y(t)-x(t)]=0. При этом: M[y(t)-x(t)]= y(t)-x(t). Дисперсия β(t) будет представлять его алгебраическую сумму, если W(jω)=e^(jωτ₀)-идеальная задержка. Поэтому дисперсия: D_β=2[R_Х(0)- R_Х(τ₀)]. Если на входе будет белый шум, то: D_βб.ш.=2D_б.ш. x(t)-белый шум на входе, y(t)- белый шум на выходе: они некоррелированы, следовательно алгебраическая сумма двух белых шумов. Динамич. и случайная погрешность характеризуется дисперсиями, следовательно важно найти оптимум, т.е. случайная погрешность должна быть минимальна. D_{СЛУЧ.ПОГР}→ D/(n-1);(n-1)=t_{УСРЕДНЕНИЯ}; D_{βДИНАМИЧ.ПОГР.}→t_{УСРЕДНЕНИЯ}

3.Фазометр с перекрытием

Это двухполупериодная схема. U1=A1sinωt, U2=A2sin[ωt+ϕ]; 1-инвертор; &-двухкодовые линии; на выходе - широтно-импульсный сигнал. В ШИМ можно преобразовать в напряжение или в цифру. Для преобразования в напряжение необходима следующая цепочка: ШИМ→нормализатор амплитуды цифрового сигнала→ФНЧ(сглаживает сигнал)→U( ). 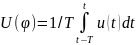, где Т-оператор сглаживания. Функция нормализатора – логическим уровням 0 и 1 присваивать жесткие или нормированные значения. Фазовый сдвиг: =360^оn/N, где n-кол-во импульсов нашей частоты через сигнал, N-частота заполнения. Фазовая характеристика фазометра с перекрытием:

0-180^о – растущий, 180^о -360^о – падающий. Она неоднозначна на цикле(2π или 360^о период) фазы (нельзя сказать, где находится эта точка). Плюсы: хорошо работает при малых соотношениях сигнал/шум. Временная диаграмма, квазигармонический сигнал: (с инвертора – прямой опорный инвертированный)

Билет №4 1.Эргодичность и стационарность СП

Стационарность – это неизменность характеристик СП во времени по аргументу. Стационарным СП в узком (строгом) смысле называют такой случайный СП, у которого все конечные функции распределения инвариантны относительно сдвига во времени, те при любом n и t0 справедливо: F(x1,x2…xn; t1,t2…tn)= F(x1,x2…xn; t1+t0,t2+t0…tn+t0)

Стационарность в широком смысле: СП называют стационарным в широком смысле (или по Хинчину, или слабо стационарный) - это такой СП, у которого мат ожидание=const, дисперсия=const, а ковар ф-ия инварианта относительно времени, а зависит только от сдвига времени равного τ=t2-t1: K_x(t1,t2)= K_x(τ), R_x(t1,t2)= R_x(τ). Таким образом стационарный в широком смысле СП является частным случаем СП в узком смысле. Стационарность в широком и узком смысле совпадает для нормальных СП.

Стационарный процесс называется эргодическим в строгом смысле, если с вероятностью P=1 все его характеристики могут быть получены по одной реализации (результаты усреднения по времени совпадают с результатами усреднения по ансамблю). Стационарный процесс не всегда является эргодическим, например квазигармонический стационарный процесс: x(t)=A(t)cos[ωt+φ(t)]. Если φ(t) неограничен, то это неэргодический СП. Если 0 2π, те задано на цикле, то это эргодический СП.