4.5 Проектировочный расчет валов
входной вал
d³ =25,3 мм;
Принимаем диаметр под подшипник dп=45 мм (с учетом размещения на валу муфты);
промежуточный вал
d³ =29,2 мм;
Принимаем диаметр под подшипник dп=30 мм;
выходной вал
d³ =36,4 мм;
Принимаем диаметр под подшипник dп=40 мм (с учетом действия на вал окружной силы цепной передачи Ft=1768,12 Н).
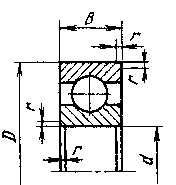
4.6 Выбор подшипников
входной вал
Принимаем шарикоподшипники радиально-упорные однорядные со скосом на одном из колец № 46309 ГОСТ 831-75
d=45 мм; D=100 мм; B=25 мм; C=48100 Н; =37700 Н;
промежуточной вал
Принимаем шарикоподшипники радиально-упорные однорядные со скосом на одном из колец № 46306 ГОСТ 831-75
d=30 мм; D=72 мм; B=19 мм; C=25600 Н; =18700 Н;
выходной вал
Принимаем шарикоподшипники радиальные однорядные № 308 ГОСТ 8338-75
d=40 мм; D=90 мм; B=23 мм; C=31900 Н; =22700 Н;
4.7Расчет основных размеров корпуса и крышки
4.7.1Конструирование основных элементов корпуса
Толщина стенки основания корпуса
= = 4,3 мм ,
где - максимальный вращающий момент на тихоходном валу.
Принимаем s=6 мм.
Толщина стенки крышки корпуса
= 0,9·6=5,4 мм.
Принимаем =6 мм.
Рисунок - Размеры верхнего пояса фланца основания корпуса и фланца крышки корпуса
…………………..
4.7.2Конструирование вспомогательных элементов корпуса
Размеры проушин
- толщина проушины
S = 2s = 2·6 = 12 мм.
Принимаем S=12 мм.
……………..
5Проверочные расчеты
5.1Расчет конической прямозубой передачи(1-2)
2 Проверочный расчет
2.1 Проверка на усталостную прочность
Расчетное условие:
==536,36 МПа (см. проектировочный расчет)
Рассчитываем контактное напряжение в полюсе зацепления при номинальной нагрузке
,
где 
- коэффициент, учитывающий форму
сопряженных поверхностей зубьев;
- коэффициент, учитывающий механические
свойства материалов сопряженных зубчатых
колес;
- коэффициент, учитывающий суммарную
длину контактных линий;
- коэффициент переменности шага.
=1,77
(для прямозубых колес при
=20°);
=275 (сочетание материалов сталь-сталь);
,
===
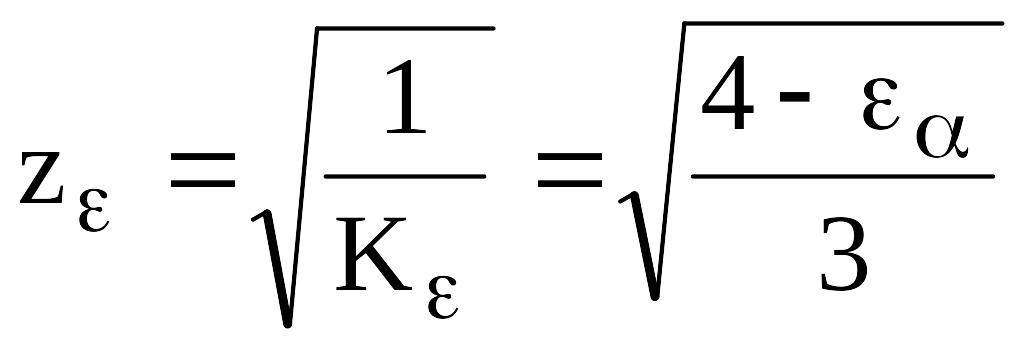1,731,
== 0,87
По известным параметрам передачи уточняем значения коэффициентов
Расчет коэффициентов ведем по средним диаметрам зубчатых колес
=59,94 мм (см. выше)
=140,00-24·0,8479=95,91 мм;
,
где - конусное расстояние (длина дистанции) в зацеплении конических зубчатых колес,
= = 82,55 мм
=1– = 0,71
при = = 0,27,
=
1,09 [3, табл. 20]
0,006
(зубчатые колеса прямозубые,
прирабатывающиеся) [3, табл. 22]
56 [3,
табл. 21]
=
==
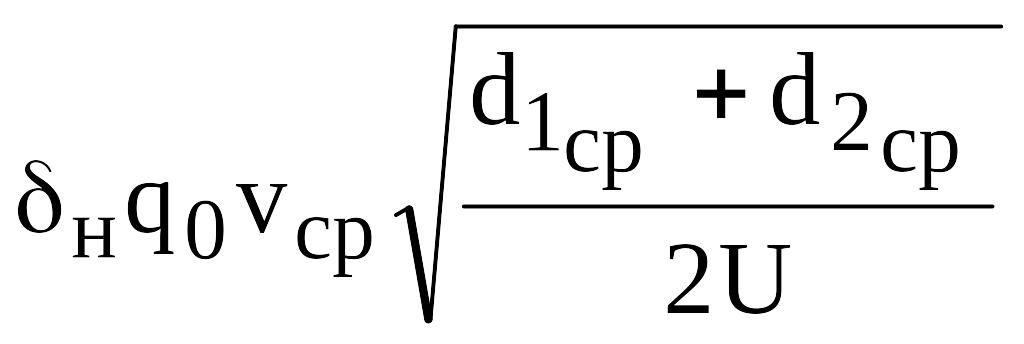5,3
,
принимаем
=5,3
(т.к.
не превышает величину
); [3,
табл. 23]
=
=
=102,1
;
==1,1
= =1,1·1,09=1,2
=
512 МПа.
512<536,36 – контактная выносливость обеспечена.
2.2 Проверка на изгибную усталостную прочность
Расчетное условие:
Допускаемое изгибное напряжение определяем по формуле
,
где 
=
- предел контактной выносливости при
эквивалентном числе циклов нагружения;
=
- коэффициент безопасности;
- коэффициент, учитывающий нестабильность свойств материала зубчатого колеса;
- коэффициент, учитывающий способ получения заготовки зубчатого колеса;
- коэффициент, учитывающий чувствительность
материала к концентрации напряжений;
- коэффициент, учитывающий шероховатость
переходной поверхности;
- коэффициент, учитывающий размеры
зубчатого колеса;
- предел выносливости при отнулевом цикле изгиба;
- коэффициент, учитывающий влияние шлифования переходной поверхности;
- коэффициент, учитывающий влияние деформационного упрочнения или электрохимической обработки переходной поверхности;
- коэффициент, учитывающий влияние двухстороннего приложения нагрузки;
- коэффициент долговечности.
,
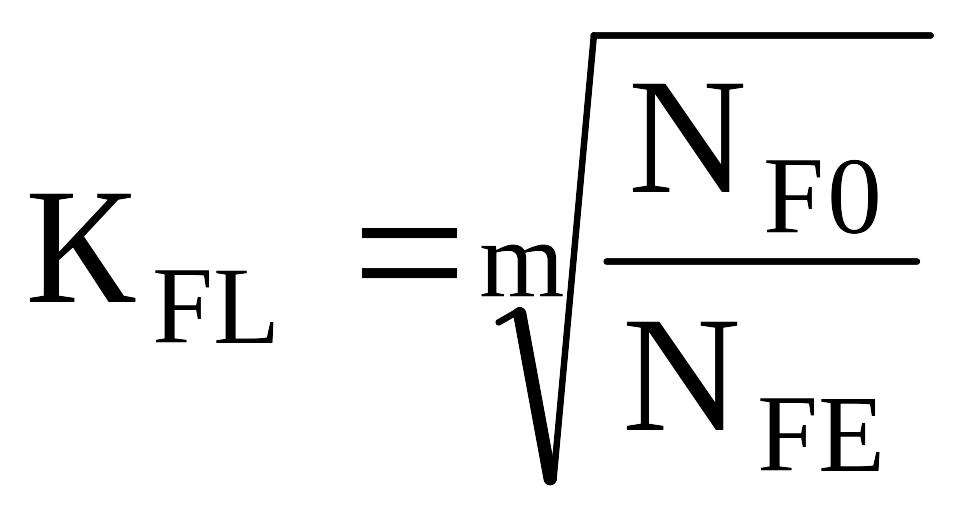где 
- базовое число циклов перемены напряжений,
соответствующее длительному пределу
выносливости;
- эквивалентное число циклов перемены
напряжений;
m – показатель степени.
Принимаем:
=1 (модуль m=2,5 мм);
=1 (принято Rа=1,25…0,63);
=1 (диаметр колес < 500 мм);
=1 (переходная поверхность не шлифуется);
=1 (деформационное упрочнение переходной поверхности не предусматривается);
=1 (приложение нагрузки одностороннее).
Изгибная прочность зубьев шестерни и
колеса в общем случае разная, поэтому
для дальнейшего расчета необходимо
установить «слабый» элемент, для чего
и для шестерни и для колеса рассчитываем
отношение
,
а «слабым» элементом будет то зубчатое
колесо пары, для которого данное отношение
меньше.
Допускаемое изгибное напряжение для шестерни:
=4
(для всех сталей)
m = 6 (для зубчатых колес с твердостью поверхности зубьев НВ=<350)
=
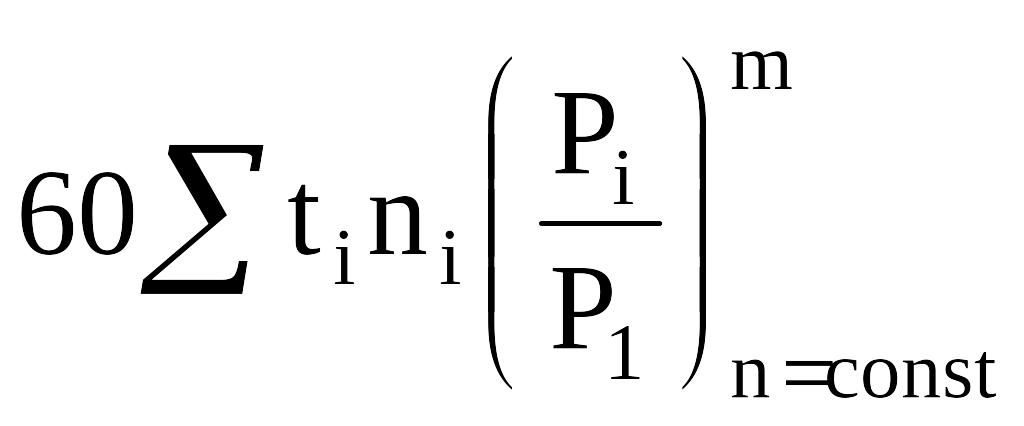= = 295
.
===
0,49 <1,принимаем
=1.
=2,2 (вероятность неразрушения свыше 0,99) [3, табл. 24]
=1 (способ получения заготовки поковка)
=2,2·1= 2,2
=1,8HB=1,8·280= 504 МПа [3, табл. 24]
=
= 504 МПа.
== 229 МПа.
Допускаемое изгибное напряжение для колеса:
Предел контактной выносливости при эквивалентном числе циклов нагружения
=4 (для всех сталей)
= = 184 ;
m = 6 (для зубчатых колес с твердостью поверхности зубьев НВ=<350)
=== 0,53 <1,принимаем =1.
=2,2 (вероятность неразрушения свыше 0,99) [3, табл. 24]
=1 (способ получения заготовки поковка)
=2,2·1= 2,2
=1,8HB=1,8·260= 468 МПа [3, табл. 24]
= = 468 МПа
Допускаемое изгибное напряжение
== 213 МПа.
Определяем более «слабый» элемент
- безразмерный коэффициент, величина
которого зависит от формы зуба (ширины
основания, фактической высоты головки,
ножки зуба, фактического угла зацепления,
формы галтели). Значение коэффициента
принимается по ГОСТ 21354-75.
=3,8 (= = = =41) [3, табл. 4]
=3,6 (= = = =106) [3, табл. 4]
= = 60; = = 59.
Более «слабым» элементом является колесо 2, по которому и ведется дальнейший расчет.
Расчетное изгибное напряжение при номинальной нагрузке определяем по формуле
==,
где 
- коэффициент, учитывающий распределение
нагрузки по ширине венца;
- коэффициент динамичности нагрузки.
Принимается: ==3,6 (см. выше)
при = =0,27, = 1,2 [3, табл. 20]
56 [3, табл. 21]
0,016
(зубчатые колеса прямозубые) [3, табл.
22]
=
==14
,
принимаем =14 (т.к. не превышает величину ); [3, табл. 23]
=
=
=112,4
;
=
=
1,12.
Остальные данные см. проектировочный расчет.
= = 175 МПа.
175<213 – изгибная выносливость обеспечена.
2.3 Проверка на контактную прочность при действии максимальных перегрузок
Расчетное условие:
Максимальное контактное напряжение
,
где 
=
512 МПа (см. выше);
- коэффициент перегрузки,
=
=
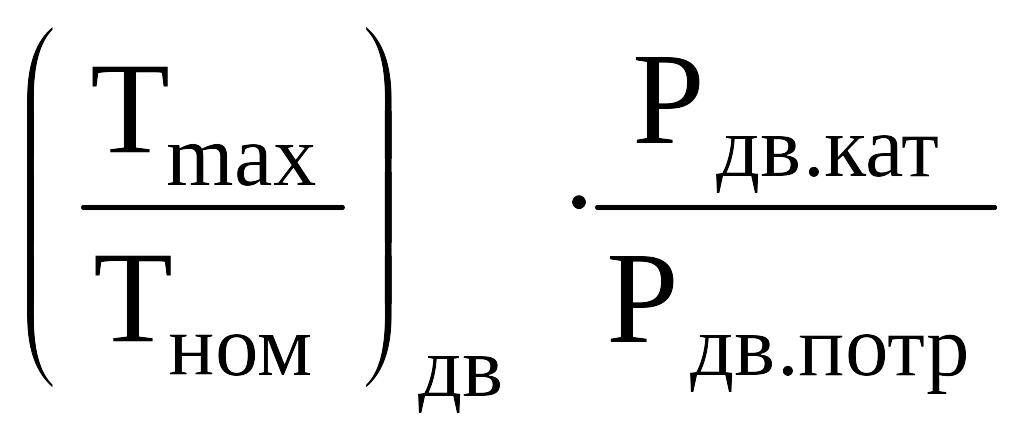= 2,22
=
= 763 МПа.
Допускаемое контактное напряжение
=2,8бт=2,8·600=
1680 МПа
763 < 1680 – контактная прочность при действии максимальных перегрузок обеспечена.
2.4 Проверка на изгибную прочность при действии максимальных перегрузок
Расчетное условие:
Максимальное изгибное напряжение
,
где = 175 МПа (см. выше);
= 2,22 (см. выше)
=
= 389 МПа.
Допускаемое изгибное напряжение
=2,75HB=2,75·260=
715 МПа,
389 < 715 – изгибная прочность при действии максимальных перегрузок обеспечена.