
- •Геометрический и физический смысл производной Тангенс угла наклона касательной прямой
- •Скорость изменения функции
- •16. Правило Лопиталя
- •17. Нахождение с помощью производной промежутков монотонности, точек экстремума и экстремумов функции
- •24. Интегрирование по частям.
- •25. Интегрирование рациональных, дробно-рациональных (метод неопределенных коэффициентов) функций. Метод разложение числителя
- •Метод подведения под знак дифференциала для простейших дробей
- •Метод выделения полного квадрата
- •Подведение числителя под знак дифференциала
- •Интегрирование правильной дробно-рациональной функции
- •Интегрирование неправильной дробно-рациональной функции
- •26. Интегрирование некоторых иррациональных функций. Интегралы от корней. Типовые методы и приемы решения
- •27. Интегрирование тригонометрических функций. Использование тригонометрических формул
- •Понижение степени подынтегральной функции
- •Метод замены переменной
- •Универсальная тригонометрическая подстановка
- •28. Определенный интеграл: определение, основные свойства, геометрический смысл.
- •29. Формула Ньютона-Лейбница
29. Формула Ньютона-Лейбница

31
Приложения определенного интеграла.
1. Вычисление площади криволинейной трапеции.

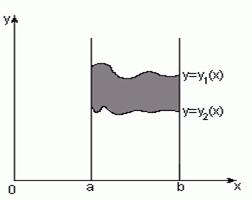
![]()

2. Вычисление объёмов тела, площади сечения которых известны.

Пусть для некоторого тела в пространстве известно значение S(x) – площади сечения этого тела плоскостью, проходящей через точку x’ и параллельной плоскости OYZ.
Тогда объём этого
тела может быть вычислен по формуле

3. Вычисление длинны дуги плоской кривой.
Пусть кривая Г
задана на плоскости OXY
уравнением y=y(x),
![]() и
и
![]()
Тогда длинна этой кривой может быть вычислена по формуле:

4. Вычисление площади поверхностей вращения плоской кривой вокруг неподвижной оси.
Пусть кривая Г,
заданная как и выше уравнением y=y(x),
,
![]() вращается вокруг оси OX.
Тогда площадь поверхности вращения
этой кривой может быть вычислена по
формуле:
вращается вокруг оси OX.
Тогда площадь поверхности вращения
этой кривой может быть вычислена по
формуле:

32
12.1.1.
Определение несобственного интеграла
по бесконечному промежутку.
Пусть функция f(x)
определена на полуоси
![]() и
интегрируема по любому отрезку [a,b],
принадлежащему этой полуоси. Предел
интеграла
и
интегрируема по любому отрезку [a,b],
принадлежащему этой полуоси. Предел
интеграла
 при
при
![]() называется
несобственным интегралом функции f(x)
от a
до
называется
несобственным интегралом функции f(x)
от a
до
![]() и
обозначается
и
обозначается
 .
.
![]() Итак,
по определению,
Итак,
по определению,
 .
Если этот предел существует и конечен,
интеграл
называется
сходящимся; если предел не существует
или бесконечен, интеграл называется
расходящимся.
Примеры:
1.
.
Если этот предел существует и конечен,
интеграл
называется
сходящимся; если предел не существует
или бесконечен, интеграл называется
расходящимся.
Примеры:
1.
 ;
этот предел не существует; следовательно,
исследуемый интеграл расходится.
Аналогично
интегралу с бесконечным верхним пределом
интегрирования определяется интеграл
в пределах от
;
этот предел не существует; следовательно,
исследуемый интеграл расходится.
Аналогично
интегралу с бесконечным верхним пределом
интегрирования определяется интеграл
в пределах от
![]() до
b
:
до
b
:
 и
в пределах от
до
:
и
в пределах от
до
:
 .
.
сходится
тогда и только тогда, когда для любого
c,
удовлетворяющего неравенству c
> a,
сходится интеграл

12.1.2. Формула Ньютона-Лейбница для несобственного интеграла.
![]() будем
обозначать
будем
обозначать
![]() ;
символом
;
символом
![]() -
соответственно,
-
соответственно,
![]() ;
тогда можно записать
;
тогда можно записать
 ,
,
 ,
,
 ,
подразумевая в каждом из этих случаев
существование и конечность соответствующих
пределов. Теперь решения примеров
выглядят более просто:
,
подразумевая в каждом из этих случаев
существование и конечность соответствующих
пределов. Теперь решения примеров
выглядят более просто:
 -
интеграл сходится;
-
интеграл сходится;
 -
интеграл расходится.
-
интеграл расходится.
Для несобственных интегралов применимы формулы интегрирования по частям и замены переменной:
 ;
при замене переменной несобственный
интеграл может преобразовываться в
собственный.
;
при замене переменной несобственный
интеграл может преобразовываться в
собственный.
33
Пусть функция f (x, y) определена в некоторой окрестности точки (x, y).
Определение.
Если существует
![]() =
=
=
=![]() ,
то он называется частной производной
(первого порядка) функции z = f
(x,
y)
по переменной x
и обозначается
,
то он называется частной производной
(первого порядка) функции z = f
(x,
y)
по переменной x
и обозначается
![]() =
=![]() =z'x
= fx'
(x,
y).
=z'x
= fx'
(x,
y).
Аналогично определяется частная производная по переменной y:
![]() =
=
![]() =
=
![]() =
=![]() =
z'y
= fy(x,y).
=
z'y
= fy(x,y).
Замечание. Из определения частных производных следует, что при вычислении переменная y считается постоянной, а при вычислении постоянной считается переменная x.
Теорема. Пусть функция f (x, y) определена вместе со своими частными производными f'x, f'у, f''xy, f''yx в некоторой окрестности точки (x0,y0), причем производные f''xy и f''yx непрерывны в этой точке, тогда f''xy (x0,y0) = f''yx (x0,y0).
Согласно этой теореме смешанные производные можно вычислять в любом порядке и нет необходимости находить обе смешанные производные.
Пусть дана функция u = f (x, y, z), определенная в некоторой области пространства Oxyz.
Определение.
Вектор с координатами
![]() ,
,
![]() ,
,
![]() называется
градиентом функции u = f
(x,
y,
z) в точке
M(x,
y,
z) и обозначается
grad u =
называется
градиентом функции u = f
(x,
y,
z) в точке
M(x,
y,
z) и обозначается
grad u =![]() +
+![]() +
+![]() .
.
Под
производной функции u = f
(x,
y,
z) в данном
направлении
![]() понимается
выражение
понимается
выражение
![]() =
cosa
+
cosb
+
cosg,
где cosa,
cosb,
cosg
– направляющие косинусы вектора
(рис.
43).
=
cosa
+
cosb
+
cosg,
где cosa,
cosb,
cosg
– направляющие косинусы вектора
(рис.
43).

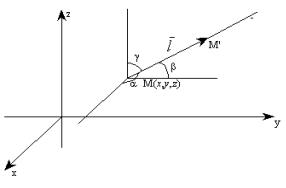 Рис.
43
Рис.
43
|
Производная представляет собой скорость изменения функции в данном направлении.
Теорема. Производная функции по направлению равна проекции градиента этой функции на данное направление (в соответствующей точке).
Величина
градиента, т.е. | grad u | = обозначается tg j и определяет крутизну
наибольшего ската или подъема поверхности
u = f (x,
y).
обозначается tg j и определяет крутизну
наибольшего ската или подъема поверхности
u = f (x,
y).
37
Определение 1. Пусть задана бесконечная числовая последовательность u1, u2,…,un,…. Выражение
называется числовым рядом. Числа u1, u2,…,un,… называются первым, вторым, …, n-м, … членами ряда. un также называется общим членом ряда. Определение 2. Сумма конечного числа n первых членов ряда называется n-ой частичной суммой ряда:
Определение
3.
Если существует конечный предел
|
Простейшие свойства числовых рядов |
Теорема 1. Если сходится ряд, полученный из ряда (1) отбрасыванием нескольких его членов, то сходится и ряд (1). Обратно, если сходится данный ряд (1), то сходится ряд, полученный из ряда (1) отбрасыванием нескольких членов. Другими словами: на сходимость ряда не влияет отбрасывание конечного числа его членов. Теорема 2. Если ряд (1) сходится и его сумма равна S, то ряд
где с – число, также сходится и его сумма равна c.S. Теорема 3. Если ряды
и
сходятся
и их суммы равны соответственно
и (u1-v1)+
(u2-v2)+…+
(un-vn)+… также сходятся
и их суммы равны соответственно
|
Признак
Даламбера:
Рассмотрим положительный
числовой ряд
![]() .
Если существует предел отношения
последующего члена к предыдущему:
.
Если существует предел отношения
последующего члена к предыдущему:
![]() ,
то:
а) При
,
то:
а) При
![]() ряд
сходится.
В частности, ряд сходится при
ряд
сходится.
В частности, ряд сходится при
![]() .
б)
При
.
б)
При
![]() ряд
расходится.
В частности, ряд расходится при
ряд
расходится.
В частности, ряд расходится при
![]() .
в)
При
.
в)
При
![]() признак
не дает ответа.
Нужно использовать другой признак. Чаще
всего единица получается в том случае,
когда признак Даламбера пытаются
применить там, где нужно использовать
предельный признак сравнения.
признак
не дает ответа.
Нужно использовать другой признак. Чаще
всего единица получается в том случае,
когда признак Даламбера пытаются
применить там, где нужно использовать
предельный признак сравнения.
Радикальный
признак Коши: Рассмотрим
положительный
числовой ряд
.
Если существует предел:
![]() ,
то:
а) При
ряд
сходится.
В частности, ряд сходится при
.
б)
При
ряд
расходится.
В частности, ряд расходится при
.
в)
При
признак
не дает ответа.
Нужно использовать другой признак.
Интересно отметить, что если признак
Коши не даёт нам ответа на вопрос о
сходимости ряда, то признак Даламбера
нам тоже не даст ответа. Но если признак
Даламбера не даёт ответа, то признак
Коши вполне может «сработать». То есть,
признак Коши является в этом смысле
более сильным признаком.
,
то:
а) При
ряд
сходится.
В частности, ряд сходится при
.
б)
При
ряд
расходится.
В частности, ряд расходится при
.
в)
При
признак
не дает ответа.
Нужно использовать другой признак.
Интересно отметить, что если признак
Коши не даёт нам ответа на вопрос о
сходимости ряда, то признак Даламбера
нам тоже не даст ответа. Но если признак
Даламбера не даёт ответа, то признак
Коши вполне может «сработать». То есть,
признак Коши является в этом смысле
более сильным признаком.
Радикальный
признак Коши обычно использует в тех
случаях, когда общий член ряда ПОЛНОСТЬЮ
находится в степени, зависящей
от «эн».
Либо когда корень
![]() «хорошо»
извлекается из общего члена ряда.
«хорошо»
извлекается из общего члена ряда.
Признак Раабе.
Пусть
![]() -
знакоположительный числовой ряд. Если
-
знакоположительный числовой ряд. Если
 ,
то числовой ряд расходится, если
,
то числовой ряд расходится, если
 ,
то ряд сходится.
,
то ряд сходится.
Признак Раабе обычно применяется тогда, когда рассмотренные выше достаточные признаки сходимости числовых рядов не приводят к результату.
Первый признак сравнения рядов.
Пусть
и
![]() -
два знакоположительных числовых ряда
и выполняется неравенство
-
два знакоположительных числовых ряда
и выполняется неравенство
![]() для
всех k
= 1, 2, 3, ...
Тогда из сходимости ряда
следует
сходимость
,
а из расходимости ряда
следует
расходимость
для
всех k
= 1, 2, 3, ...
Тогда из сходимости ряда
следует
сходимость
,
а из расходимости ряда
следует
расходимость
Второй признак сравнения.
Пусть
и
-
знакоположительные числовые ряды. Если
![]() ,
то из сходимости ряда
следует
сходимость
.
Если
,
то из сходимости ряда
следует
сходимость
.
Если
![]() ,
то из расходимости числового ряда
следует
расходимость
.
,
то из расходимости числового ряда
следует
расходимость
.
Третий признак сравнения.
Пусть
и
-
знакоположительные числовые ряды. Если
с некоторого номера N
выполняется условие
 ,
то из сходимости ряда
следует
сходимость
,
а из расходимости ряда
следует
расходимость
.
,
то из сходимости ряда
следует
сходимость
,
а из расходимости ряда
следует
расходимость
.
39
уравнение
F(x, y, y ') = 0,
где y = y(x) — неизвестная, непрерывно дифференцируема на (a,b) функция, называется обыкновенным дифференциальным уравнением первого порядка.
Функция y = y(x) называется решением дифференциального уравнения F(x, y, y ') = 0, если она непрерывно дифференцируема на (a,b) и F(x, y(x), y '(x)) ≡ 0 для всех x из (a,b) .
График решения дифференциального уравнения называют интегральной кривой дифференциального уравнения.
Дифференциальное уравнение 1–го порядка имеет бесконечно много решений. Для того чтобы выделить единственное решение, нужно задать дополнительные (начальные) условия.
Задача отыскания решения y = y(x) уравнения F(x, y, y ' ) = 0 , удовлетворяющего условию y(x0) = y0, называется задачей Коши (или начальной задачей).
Условие y(x0) = y0 — начальное условие.
Любое конкретное решение y = y(x) (решение задачи Коши) уравнения 1–го порядка, называется частным решением уравнения.
Общее решение уравнения, записанное в неявной форме Φ(x, y) = C, называется общим интегралом уравнения.
Частное решение уравнения, записанное в неявной форме Φ(x, y) = 0, называется частным интегралом уравнения.
Уравнение 1-го порядка, разрешенное относительно производной, называют уравнением, записанными в нормальной форме:
![]()
Уравнения первого порядка часто записывают в дифференциальной форме:
M(x, y)dx + N(x, y)dy = 0.
Решение такого уравнения можно искать как в виде y = y(x) , так и в виде x = x(y) .
40
Дифференциальное уравнение первого порядка y' = f(x,y) называется уравнением с разделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций, зависящих только от x и y:
![]()
где
p(x)
и h(y)
− непрерывные функции.
Рассматривая
производную y'
как отношение дифференциалов
![]() ,
перенесем dx
в правую часть и разделим уравнение на
h(y):
,
перенесем dx
в правую часть и разделим уравнение на
h(y):
![]()
Разумеется,
нужно убедиться, что h(y)
≠ 0. Если найдется число x0,
при котором h(x0)
= 0, то это число будет также являться
решением дифференциального уравнения.
Деление на h(y)
приводит к потере указанного решения.
Обозначив
![]() ,
запишем уравнение в форме:
,
запишем уравнение в форме:
![]()
Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение:
![]()
где C − постоянная интегрирования. Вычисляя интегралы, получаем выражение
![]()
описывающее общее решение уравнения с разделяющимися переменными.
44
Дифференциальное
уравнение второго порядка имеет вид
![]() .
.
Определение.
Общим решением уравнения второго порядка
называется такая функция
![]() ,
которая при любых значениях
,
которая при любых значениях
![]() и
и
![]() является
решением этого уравнения.
является
решением этого уравнения.
Определение.
Линейным однородным уравнением второго
порядка называется уравнение
![]() .
Если коэффициенты
.
Если коэффициенты
![]() и
и
![]() постоянны,
т.е. не зависят от
постоянны,
т.е. не зависят от
![]() ,
то это уравнение называют уравнением
с постоянными коэффициентами и записывают
его так:
,
то это уравнение называют уравнением
с постоянными коэффициентами и записывают
его так:
![]() .
.
Уравнение
![]() будем
называть линейным неоднородным
уравнением.
будем
называть линейным неоднородным
уравнением.
Определение.
Уравнение
![]() ,
которое получается из линейного
однородного уравнения заменой функции
,
которое получается из линейного
однородного уравнения заменой функции
![]() единицей,
а
единицей,
а
![]() и
и
![]() -
соответствующими степенями
-
соответствующими степенями
![]() ,
называется характеристическим уравнением.
,
называется характеристическим уравнением.
Известно,
что квадратное уравнение
имеет
решение, зависящее от дискриминанта
![]() :
:
![]() ,
т.е. если
,
т.е. если
![]() ,
то корни
,
то корни
![]() и
и
![]() -
действительные различные числа. Если
-
действительные различные числа. Если
![]() ,
то
,
то
![]() .
Если же
.
Если же
![]() ,
т.е.
,
т.е.
![]() ,
то
,
то
![]() будет
мнимым числом, а корни
и
-
комплексными числами. В этом случае
условимся обозначать
будет
мнимым числом, а корни
и
-
комплексными числами. В этом случае
условимся обозначать
![]() .
.
