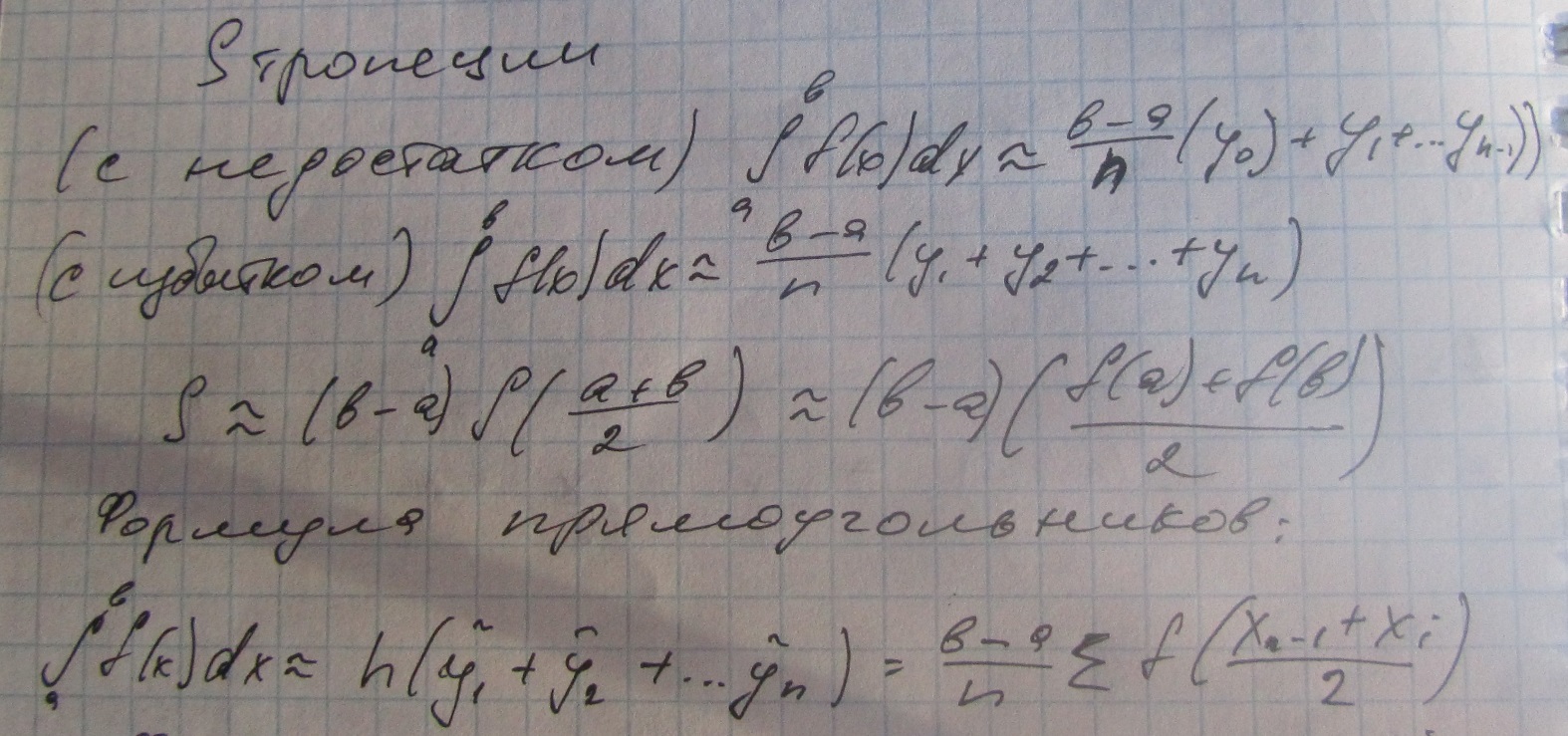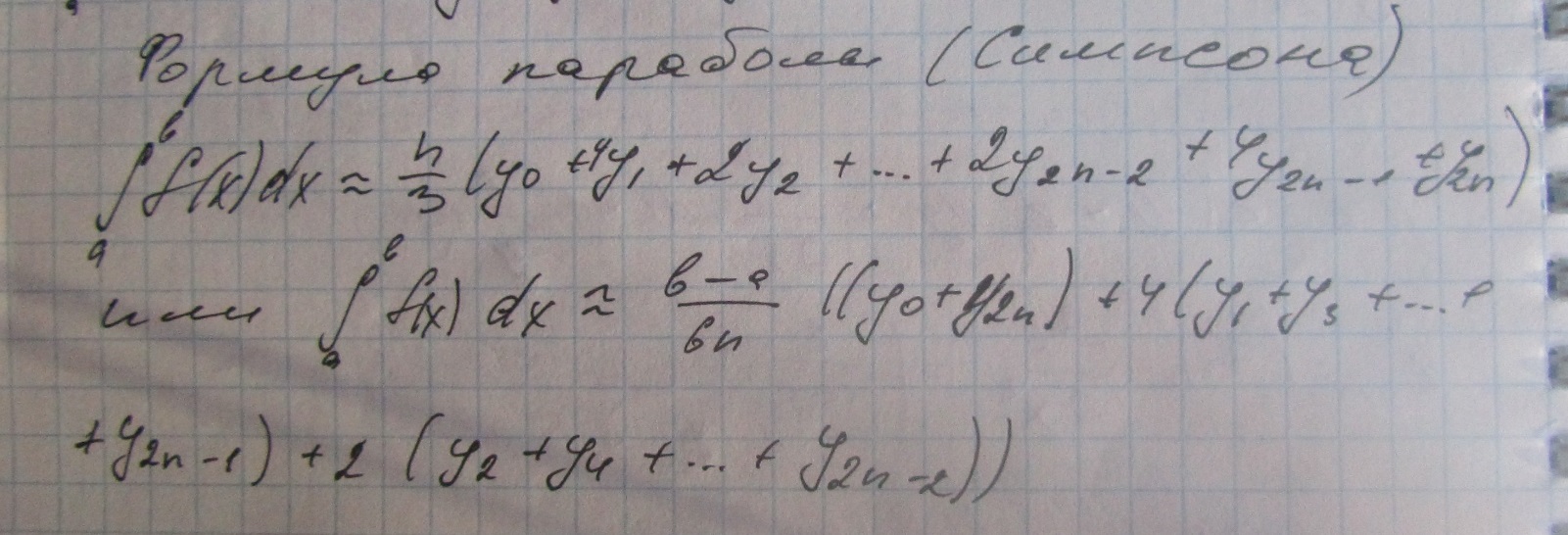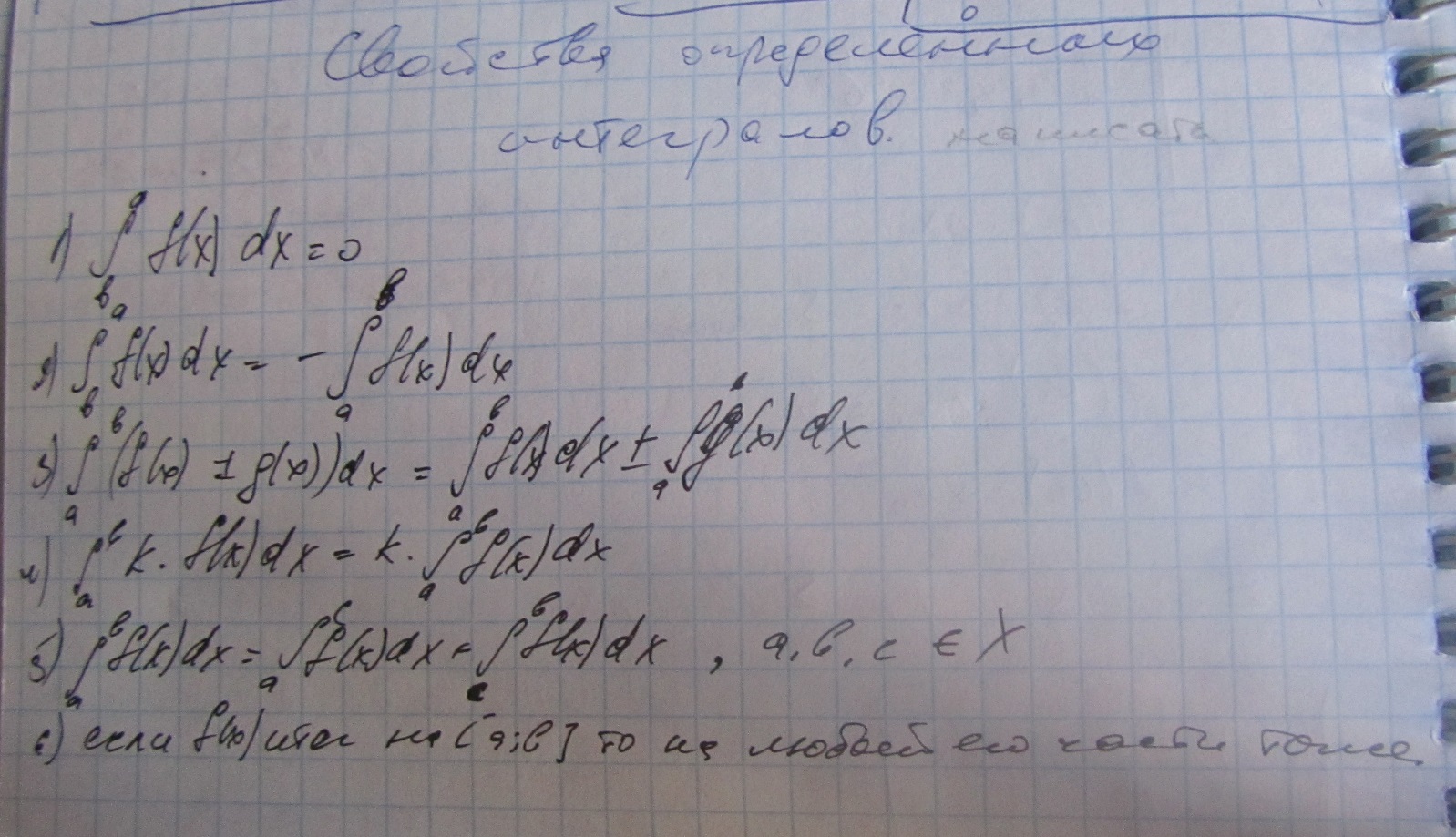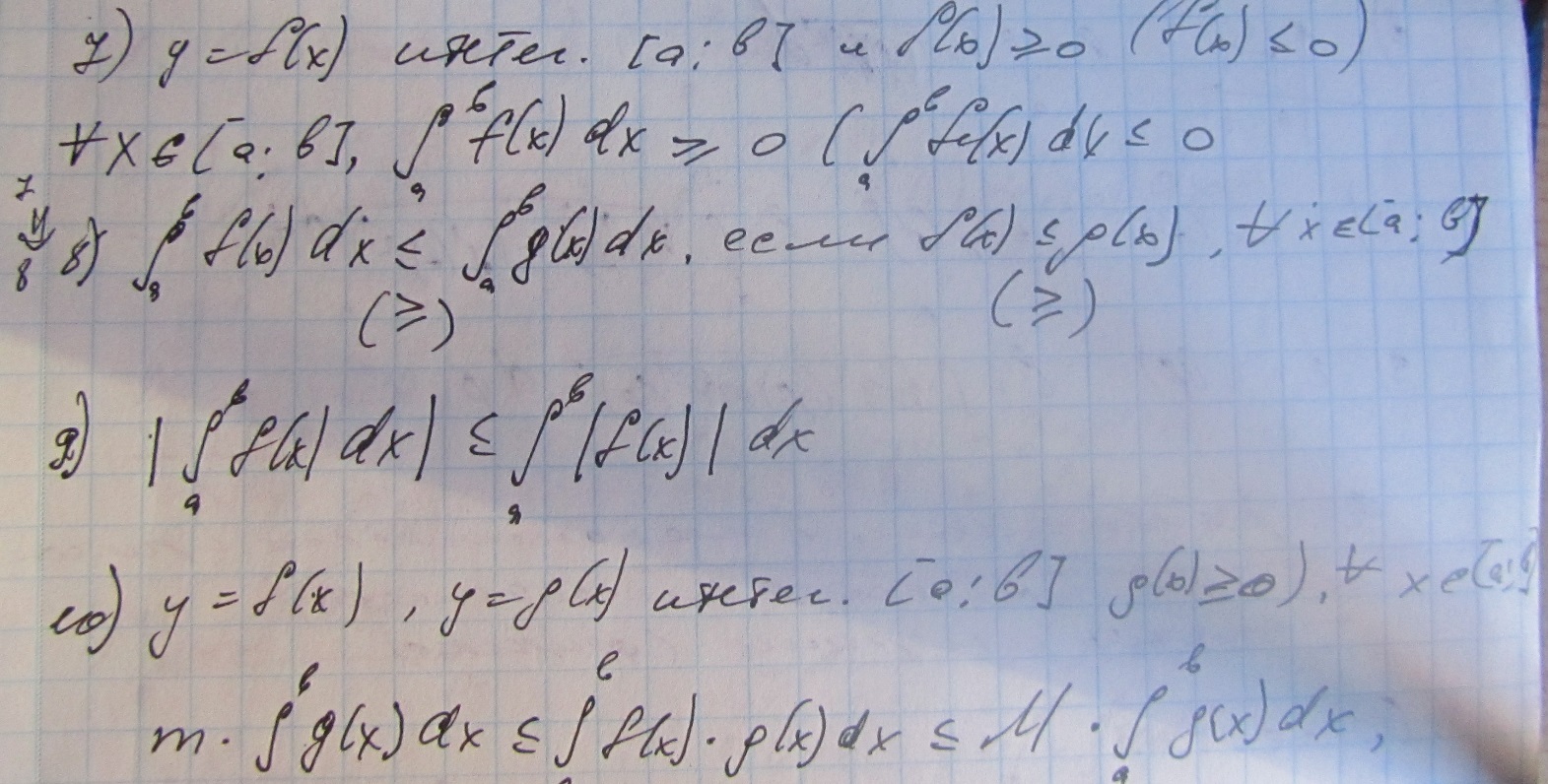Универсальная тригонометрическая подстановка

Универсальная тригонометрическая подстановка – это частый случай метода замены переменной. Её можно попробовать применить, когда «не знаешь, что делать». Но на самом деле есть некоторые ориентиры для ее применения. Типичными интегралами, где нужно применить универсальную тригонометрическую подстановку, являются следующие интегралы: , , ,  и т.д.

Пример 17

Найти неопределенный интеграл.

Универсальная тригонометрическая подстановка в данном случае реализуется следующим способом. Проведем замену: . Я использую не букву , а букву , это не является каким-то правилом, просто опять же я так привык решать.

Здесь удобнее находить дифференциал , для этого из равенства , я выражаю : Навешиваю на обе части арктангенс: Арктангенс и тангенс взаимно уничтожаются:

Таким образом:

На практике можно не расписывать так подробно, а просто пользоваться готовым результатом:

! Выражение  справедливо только в том случае, если под синусами и косинусами у нас просто «иксы», для интеграла  (о котором мы еще поговорим) всё будет несколько иначе!

При замене  синусы и косинусы у нас превращаются в следующие дроби: , , эти равенства основаны на известных тригонометрических формулах: ,

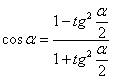
Итак, чистовое оформление может быть таким:

Проведем универсальную тригонометрическую подстановку:

(1) Производим в исходный интеграл подстановку: , , .

(2) Приводим знаменатель к общему знаменателю.

(3) Избавляемся от четырехэтажности дроби, при этом  у нас сокращается. Раскрываем скобки в знаменателе, двойку в числителе выносим за знак интеграла.

(4) Приводим подобные слагаемые в знаменателе.

(5) Интеграл  решается методом выделения полного квадрата.  Более подробно с этим методом можно ознакомиться на уроке Интегрирование некоторых дробей. Разложение  является подготовкой для осуществления вышеуказанного приёма

(6) Выделяем полный квадрат и готовим интеграл для интегрирования.

(7) Интегрируем по табличной формуле .

(8) Проводим обратную замену, вспоминая, что .

Готово.

28. Определенный интеграл: определение, основные свойства, геометрический смысл.

В общем виде определенный интеграл записывается так: Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования.

Нижний предел интегрирования стандартно обозначается буквой . Верхний предел интегрирования стандартно обозначается буквой . Отрезок  называется отрезком интегрирования.

Этапы решения определенного интеграла следующие:

1) Сначала находим первообразную функцию  (неопределенный интеграл). Обратите внимание, что константа  в определенном интеграле никогда не добавляется. Обозначение   является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись ?  Подготовка для применения формулы Ньютона-Лейбница.

2) Подставляем значение верхнего предела в первообразную функцию: .

3) Подставляем значение нижнего предела в первообразную функцию: .

4) Рассчитываем (без ошибок!) разность , то есть, находим число.