3.Понятие производной функции, геометрический и механический смысл.

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

Геометрический и физический смысл производной Тангенс угла наклона касательной прямой

Геометрический смысл производной. На графике функции выбирается абсцисса x₀ и вычисляется соответствующая ордината f(x₀). В окрестности точки x₀ выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C₅). Расстояние Δx = x — x₀ устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C₅ — C₁). Тангенс угла α наклона этой касательной — и есть производная в точке x₀.

Если функция имеет конечную производную в точке то в окрестности её можно приблизить линейной функцией

Функция называется касательной к в точке Число является угловым коэффициентом или тангенсом угла наклона касательной прямой.

Скорость изменения функции

Пусть  — закон прямолинейного движения. Тогда выражает мгновенную скорость движения в момент времени Вторая производная выражает мгновенное ускорение в момент времени

Вообще производная функции в точке выражает скорость изменения функции в точке , то есть скорость протекания процесса, описанного зависимостью

4.Уравнение касательной и нормали к кривой

Если функция  дифференцируема в точке , то уравнение касательной к графику этой функции в точке с абсциссой  имеет вид

.

Уравнение нормали к графику функции f (x) в точке x0, при условии, что f '(x0) ≠ 0 имеет вид:

5.Правила дифференцирования. Таблица производных.

6.Производная сложной функции и обратной функции.

Производная сложной функции находится по такому правилу:

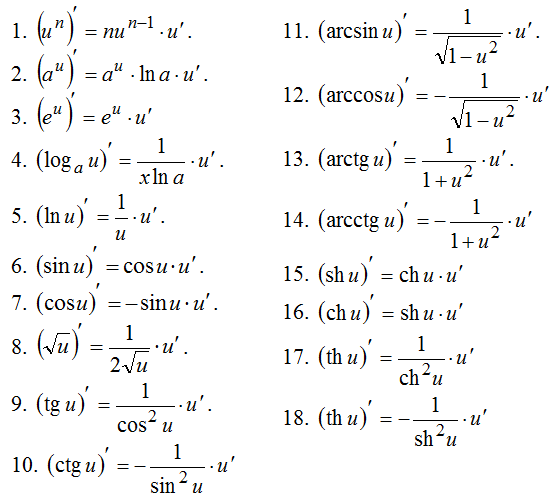
правило нахождения производной обратной функции.

Пусть функции y = f(x) и x = g(y) взаимно обратные, определенные на интервалах и соответственно. Если в точке существует конечная отличная от нуля производная функции f(x), то в точке существует конечная производная обратной функции g(y), причем . В другой записи .

Можно это правило переформулировать для любого x из промежутка , тогда получим .

7.Дифференциал функции. Геометрический смысл д.ф. Основные понятия.

Дифференциалом функции называется линейная относительно часть приращения функции. Она обозначается как или . Таким образом:

Наряду с понятием дифференциала функции вводится понятие дифференциала аргумента. По определению дифференциал аргумента есть приращение аргумента:

Дифференциал dу называют также дифференциалом первого порядка.

дифференциал функции у=ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.

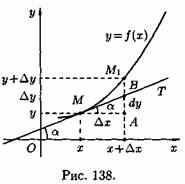
В этом и состоит геометрический смысл дифференциала.

8.Основные теоремы о дифференциалах. Инвариантность формы первого дифференциала.

Теорема 1. Дифференциал суммы, произведения и частного двух дифференцируемых функций определяются следующими формулами:

Теорема 2. Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.

Пусть у=ƒ(u) и u=φ(х) две дифференцируемые функции, образующие сложную функцию у=ƒ(φ(х)). По теореме о производной сложной функции можно написать

у'_х=у'_u•u'_x.

Умножив обе части этого равенства на dx, поучаем у'_хdx=у'_u•u'_хdx. Но у'_хdx=dy и u'_хdx=du. Следовательно, последнее равенство можно переписать так:

dy=у'_udu.

Сравнивая формулы dy=у'_х•dx и dy=у'_u•du, видим, что первый дифференциал функции у=ƒ(х) определяется одной и той же формулой независимо от того, является ли ее аргумент независимой переменной или является функцией другого аргумента.

Это свойство дифференциала называют инвариантностью (неизменностью) формы первого дифференциала.

Формула dy=у'_х•dx по внешнему виду совпадает с формулой dy=у'_u•du, но между ними есть принципиальное отличие: в первой формуле х — независимая переменная, следовательно, dx=∆х, во второй формуле и есть функция от х, поэтому, вообще говоря, du≠∆u.

9.Таблица дифференциалов. Производные и дифференциалы высших порядков. Применение дифференциалов к приближенным вычислениям.

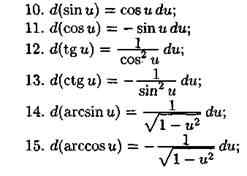
производной n–го порядка функции f(x), называется производная от производной функции f(x)   (n − 1)–го порядка. Производная n–го порядка обозначается f(n) (x).

Функция, имеющая в точке производную n–го порядка, называется n раз дифференцируемой в этой точке.

Функция, имеющая в точке производные всех порядков, называется бесконечно дифференцируемой в этой точке.

Если речь идет о производной n–го порядка ( n = 2, 3, … ) в фиксированной точке x0, то для существования f(n) (x0) необходимо существование f(n − 1) (x) не только в точке x0, но и в некоторой ее окрестности.

( u + v )(n) = u(n) + v(n) ,

 

а производная n–го порядка произведения определяется формулой Лейбница

 

где

Дифференциал от первого дифференциала, при условии, что повторное приращение независимой переменной x совпадает с первоначальным, называется вторым дифференциалом функции f(x) в точке x и обозначается d2 f(x).

Дифференцируем выражение в правой части (1) как произведение

 

d2 f(x) = d (df(x) ) = d (f'(x) dx) = f''(x) dx · dx + f'(x) · d(dx) .

 

Учитывая, что d (dx) = 0, получаем формулу для вычисления второго дифференциала

 

d2 f(x) = f ''(x) dx2 .

(2)

 

Пусть в интервале (a, b) функция f(x) имеет производные до n–го порядка включительно.

Дифференциалом n–го порядка называется дифференциал от дифференциала (n − 1)–го порядка

 

dn f(x) = d (d(n − 1) f(x)).

 

Формула для вычисления дифференциала n–го порядка

 

dn f(x) = f(n) (x) dxn .

Применение дифференциала к приближенным вычислениям

Как уже известно, приращение ∆у функции у=ƒ(х) в точке х можно представить в виде ∆у=ƒ'(х)•∆х+α•∆х, где α→0 при ∆х→0, или ∆у=dy+α•∆х. Отбрасывая бесконечно малую α•∆х более высокого порядка, чем ∆х, получаем приближенное равенство

∆у≈dy

причем это равенство тем точнее, чем меньше ∆х.

Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.

Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула широко применяется в вычислительной практике.

Подставляя в равенство значения ∆у и dy, получим

ƒ(х+∆х)-ƒ(х)≈ƒ'(х)∆х

или

ƒ(х+∆х)≈ƒ(х)+ƒ'(х)•∆х.                           

Формула используется для вычислений приближенных значений функций.

10. Формула Тейлера. Формула Маклорена. Пять основных разложений.

Рассмотрим многочлен -й степени

Его можно представить в виде суммы степеней , взятых с некоторыми коэффициентами. Продифференцируем его раз по переменной , а затем найдем значения многочлена и его производных в точке

выражение называется формулой Маклорена для многочлена степени .

можно разложить многочлен по степеням разности , где - любое число. В этом случае будем иметь:

Это выражение называется формулой Тейлора для многочлена в окрестности точки .

Для произвольной функции , не являющейся многочленом, формула Тейлора в окрестности некоторой точки принимает вид:

Последнее слагаемое называется остаточным членом в форме Пеано.

Замечание

Формула Маклорена является частным случаем формулы Тейлора при .

Пять основных разложений 1)y=e^x, x₀=0

2) y=sinx, x₀=0

3) y=cosx, x₀=0

4) y=ln(1+x), x₀=0

5) y=(1+x)^p, x₀=0

Если р – натуральное, то y⁽ⁿ⁾(0)=0 np+1 (либо n<p, если p-натуральное)

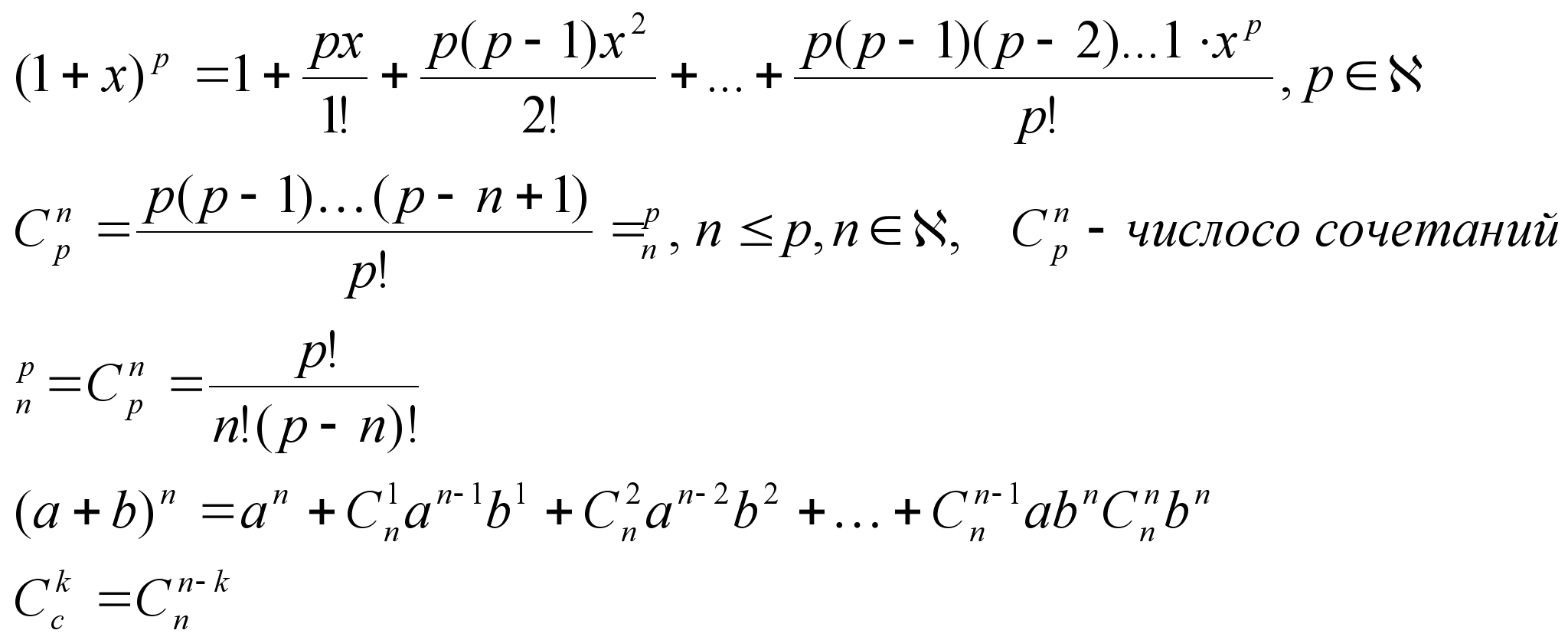
11. Некоторые теоремы о дифференцируемых функциях.

Теорема. Ролля. Если функция g(x) непрерывна на отрезке [a,b], дифференцируема во всех внутренних точках этого отрезка и на концах обращается в нуль g(a)=g(b)=0, то существует по крайней мере одна точка a < c < b в которой производная g обращается в нуль g(c)=0.

Теорема. Лагранжа. Если функция g(x) непрерывна на отрезке [a,b], дифференцируема во всех внутренних точках этого отрезка, то существует по крайней мере одна точка a < c < b в которой выполняется равенство

g(b)g(a)=g(c)(ba)

Теорема. Коши. Если функции g(x) и h(x) непрерывны на отрезке [a,b], дифференцируемы во всех внутренних точках этого отрезка, причем h(x)  0 внутри отрезка [a,b], то существует точка a < c < b в которой выполняется равенство

g(b)g(a) h(b)h(a) = g(c) h(c)

Теорема. Лопиталя. Пусть функции g(x) и h(x) на некотором отрезке [a,b] удовлетворяют условиям теоремы Kоши и обращаются в 0 в точке x=a, т.е. g(a)=h(a)=0, тогда если существует предел отношения g(x)/h(x) при x a, то существует и

lim x a  g(x)/h(x)

причем

lim x a  g(x)/h(x)= lim x a  g(x)/h(x).

12. Теорема Ферма.

Великая: Для любого натурального числа уравнение

не имеет натуральных решений , и .

Малая: Если p — простое число, и не делится на , то Другими словами, при делении нацело на даёт в остатке 1.

Равносильная формулировка:

Для любого простого и целого : делится на

Ле́мма Ферма́ утверждает, что производная дифференцируемой функции в точке локального экстремума равна нулю.

13. Теорема Ролля.

Если вещественная функция, непрерывная на отрезке и дифференцируемая на интервале , принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.

14. Теорема Коши.

Теорема Коши́ о среднем значении.

Пусть даны две функции и такие, что: и определены и непрерывны на отрезке ; производные и конечны на интервале ; производные и не обращаются в нуль одновременно на интервале ; тогда существует , для которой верно: . (Если убрать условие 4, то необходимо, например, усилить условие 3: g'(x) не должна обращаться в нуль нигде в интервале .)

15. теорема Лагранжа.

Пусть функция f(x)

1. непрерывна на отрезке [a, b];

2. дифференцируема в интервале (a, b).

Тогда существует точка с О (a, b) такая, что

f(b) − f(a) = f '(c) · (b − a) .

(1)

 Формула (1) называется формулой Лагранжа, или формулой конечных приращений.