Предэкзаменационная контрольная работа Инструкция по выполнению контрольной работы по математике

На выполнение контрольной работы дается 3 астрономических часа (180 минут).

Внимательно ознакомьтесь с заданиями обязательной и дополнительной частей экзаменационной работы.

Обратите внимание, что:

– экзаменационная работа сопровождается критериями оценки;

– в обязательную часть включены наиболее простые задания, в дополнительную – более сложные;

– правильное выполнение каждого задания оценивается баллами, которые проставлены в скобках около каждого задания;

– если Вы приведете неверный ответ или ответ будет отсутствовать, будет выставлено 0 баллов.

Для получения оценки удовлетворительно (3) достаточно правильно выполнить от 11 до 15 заданий обязательной части.

После того, как Вы наберете необходимое количество баллов для получения оценки удовлетворительно (3), определите, какие задания из обязательной или дополнительной части и сколько из них Вы сможете еще выполнить для повышения удовлетворительной оценки (3) до оценок хорошо (4) или отлично (5).

Для получения оценки хорошо (4) нужно набрать не менее 16 баллов, правильно выполнив при этом хотя бы одно задание из дополнительной части.

Для получения оценки отлично (5) нужно набрать не менее 22 балла, правильно выполнив при этом не менее двух заданий из дополнительной части.

Начинайте работу с заданий обязательной части и постарайтесь сначала набрать достаточное число баллов для получения оценки удовлетворительно (3).

Выполняйте задания в предложенном порядке. Пропускайте то задание, выполнение которого Вас затрудняет, и переходите к следующему. Если останется время, Вы сможете вернуться к пропущенным заданиям.

Постарайтесь выполнить как можно больше заданий и набрать как можно больше баллов.

Желаем удачи!

Вариант 1 Обязательная часть

При выполнении заданий 1-13 запишите ход решения и полученный ответ

1. (1 балл) Сырок стоит 7 рублей 20 копеек. Какое наибольшее число сырков можно купить на 60 рублей, если цена сырка уменьшится на 10?

2. (1 балл) В равнобедренном треугольнике ABC с основанием AC боковая сторона AB равна 8, а . Найдите высоту, проведенную к основанию.

3. (1 балл) Для транспортировки 45 тонн груза на 1300 км можно использовать одного из трех перевозчиков. Стоимость перевозки и грузоподъемность автомобилей для каждого перевозчика указана в таблице. Сколько рублей придется заплатить за самую дешевую перевозку за один рейс?

Перевозчик	Стоимость перевозки одним автомобилем (руб. на 100 км)	Грузоподъемность автомобилей (тонн)
А	3200	3,5
Б	4100	5
В	9500	12

4. (1 балл) На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.

5. (1 балл) Найдите значение выражения .

6. (1 балл) Прямая параллельна касательной к графику функции . Найдите абсциссу точки касания.

7. (1 балл) Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

8. (1 балл) При температуре рельс имеет длину м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону , где — коэффициент теплового расширения, — температура (в градусах Цельсия). При какой температуре рельс удлинится на 6 мм? Ответ выразите в градусах Цельсия.

9. (1 балл) Тело движется по закону: S(t)= х²–7х+2. Определите, в какой момент времени скорость будет равна 5.

10. (1 балл) Определите, какие из перечисленных точек не принадлежат графику функции y=f(x), f(х) = 2 х² +x – 1.

А (0; –1); В (0; –1); С (2; 4); Д (1; 2).

11. (1 балл) Найти область определения функции y=lg(x²-3x+2) .

12. (1 балл) В соревнованиях по художественной гимнастике участвуют: три гимнастки из России, три гимнастки из Украины и четыре гимнастки из Белоруссии. Порядок выступления определяется жеребьёвкой. Найдите вероятность того, что первой будет выступать гимнастка из России.

13. (1 балл) Решите неравенство log₂ (2х + 10) < 4.

14. (1 балл) Определите, какой из ниже приведенных графиков соответствует нечетной функции. Отметьте его знаком «+» и кратко поясните, почему.

И

х

х

х

х

спользуя график функции у = f( ) (см. рис. ниже), определите и запишите ответ:

15. (1 балл) экстремумы функции;

16. (1 балл) при каких значениях f( ) ≥ 2.

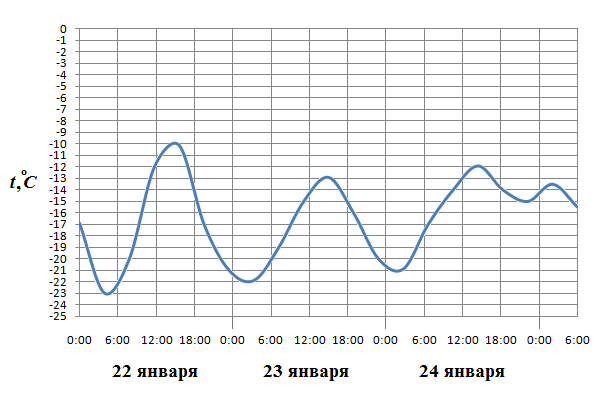
17. (1 балл) На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 22 января.

18. (1 балл) Решите уравнение sin² х + 2sin х = cos² х.