Умения к теме «Определённый интеграл»
1. Геометрический смысл определенного интеграла
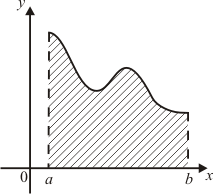
1. С помощью интеграла
вычисляется площадь фигуры, изображенной
на рисунке
1.
2.
3.
4.
Решение. Функция
на
промежутке
возрастает, при этом
.
Данному условию удовлетворяет четвертый
ответ.
2. Верно ли утверждение: “Площадь
фигуры
,
ограниченная осью Ox,
прямыми
,
и графиком функции
,
равна площади фигуры
,
ограниченной прямыми
,
,
и графиком функции
”?
Решение. Для решения данной задачи достаточно всего лишь построить фигуры (1) и (2). Мы получим две фигуры, основания и боковые стороны которых равны, а сверху обе фигуры ограничены графиками одинаковой формы. Следовательно, их площади совпадают, т.к. площадь не зависит от параллельного переноса.
Аналитически равенство площадей данных
фигур можно доказать, сравнив определённые
интегралы
и
,
значение первого равно площади фигуры
(1), значение второго соответственно
площади фигуры (2).
3. На каких из приведённых ниже рисунков изображена криволинейная трапеция?
А Б
В Г
Решение:
На рисунке А изображена криволинейная
трапеция, ограниченная графиком некоторой
функции
и прямыми
и
.
Фигура на рисунке Б не является криволинейной трапецией, так как её часть лежит ниже оси Ox.
Фигура на рисунке В также не является криволинейной трапецией, так как она полностью лежит ниже оси Ox.
На графике Г изображена криволинейная
трапеция, ограниченная графиком некоторой
функции
и прямыми
и
.
2. Интегрируемые и неинтегрируемые по Риману функции
1. Интегрируема ли по Риману функция Дирихле?
Решение. Рассмотрим функцию:
Возьмем в качестве сегмента
отрезок
Очевидно, что функция
– ограничена на
.
Покажем, что она не является интегрируемой
на
.
Рассмотрим произвольное разбиение отрезка на части.
Возьмем
,
Если функция интегрируема, то величина
предела
не зависит от выбора точек
Мы получили, что величина предела зависит от выбора точек . Значит не интегрируема на сегменте .
3. Свойства определенного интеграла
1.Найти значение интеграла
.
Решение:
.
2. Сравнить
и
.
Решение. Т.к. функция
монотонно возрастает и при
принимает отрицательные значения, а
при
лишь положительные, то очевидно, что на
промежутке
оба интеграла принимают одинаковые
отрицательные значения. Тогда достаточно
сравнить лишь интегралы
и
,
которые однозначно принимают положительные
значения. Т.к. функция
монотонно возрастает, то площадь фигуры
ограниченной ею на промежутке
будет больше, чем на промежутке
.
Следовательно,
,
а т.к. из значений обоих интегралов мы
вычитали одинаковое число, равное
значению
,
то соотношение не изменится.
.
3. Сравнить
и
.
Решение. Т.к. функции рассматриваются
на одном промежутке, то значение данных
интегралов будет зависеть от поведения
подынтегральных функций на этом
промежутке. При
принимает лишь положительные значения,
же на промежутке
положителен, а при
принимает значения меньше нуля.
Следовательно, < .
4. Вычислить, при помощи свойств
определенного интеграла:
.
Решение. Преобразуем выражение:
.
По свойствам определенного интеграла полученное выражение
.