3.10. Нахождение точных верхней и нижней границ функции нескольких переменных

1. Найти наибольшее и наименьшее значение функции

на множестве

.

Решение:

Т

Y

ак как и , т.е. константам, функция монотонна и непрерывна на всем множестве и, следовательно, принимает свои наибольшие и наименьшие значения в граничных его точках и все значения между ними в остальных точках. Изобразим область задания:

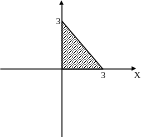
Необходимо проверить точки , , :

,

,

.

Следовательно, максимум равен 7, а минимум -8.

Ответ: , .

4.1. Исследование последовательностей на сходимость в

1. К какой точке из сходится последовательность точек

?

Решение:

Имеем:

,

(как произведение бесконечно малой функции на ограниченную).

Тогда, из связи сходимости координат и последовательности точек, получаем

.

Ответ: .

2. Из каких ниже перечисленных последовательностей возможно выделить сходящуюся подпоследовательность?

А) Б)

В) Г)

Решение:

Варианты А и В содержат неограниченные последовательности точек так как , , . Следовательно, к ним не применима теорема Больцано-Вейерштрасса. Варианты Б и Г содержат ограниченные последовательности точек так как , , при . Следовательно, по теореме Больцано-Вейерштрасса, из них возможно выделить сходящиеся подпоследовательности.

Ответ: В вариантах Б и Г.

3. Сходится ли последовательность точек ?

Решение:

Для исследования воспользуемся критерием Коши. Условие

эквивалентно условию

.

Рассмотрим каждый модуль по отдельности.

Так как и и разность двух бесконечно малых функций есть бесконечно малая функция, то по свойству бесконечно малой функции получаем

.

Однако (в силу произвольности выбора числа ) мы можем задать его например равным . Тогда найдется такое число что

что нарушает условие Коши, и, следовательно, последовательность точек расходится.

Ответ: Нет, не сходится.

4.2. Исследование существования двойного предела

1. Существует ли предел ?

Решение:

Этот предел не существует, так как последовательности сходятся к точке при в то время как соответствующие последовательности значений функции сходятся к различным предельным значениям:

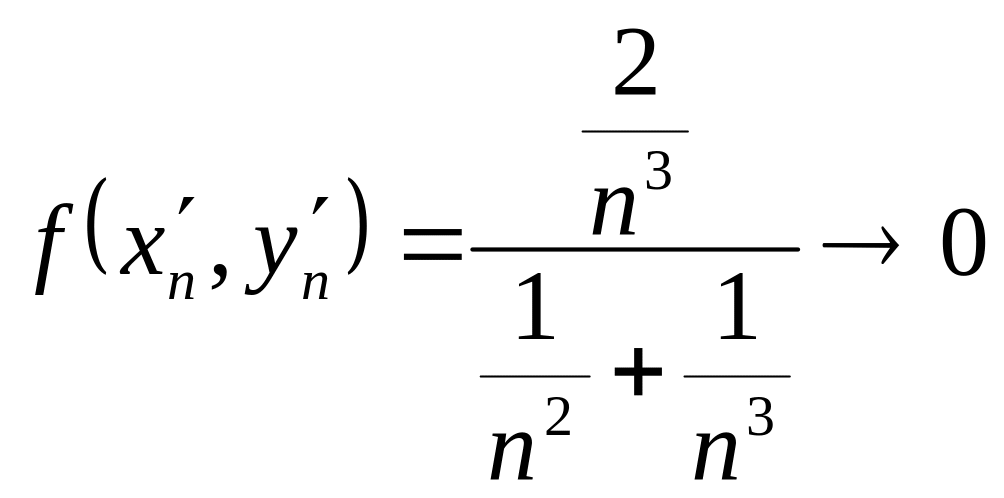
при

Ответ: не существует.

2. По каким направлениям существует конечный предел:

, если и .

Решение:

Имеем

.

Поскольку , а − ограниченная функция, то предел будет конечным, если или . В первом случае , , во втором , .

Ответ: , , , .

4.3. Исследование функции нескольких переменных на непрерывность

1. Доказать по определению на языке , что функция непрерывна в точке .

Решение:

Запишем определение непрерывности на языке :

.

1. Зафиксируем .

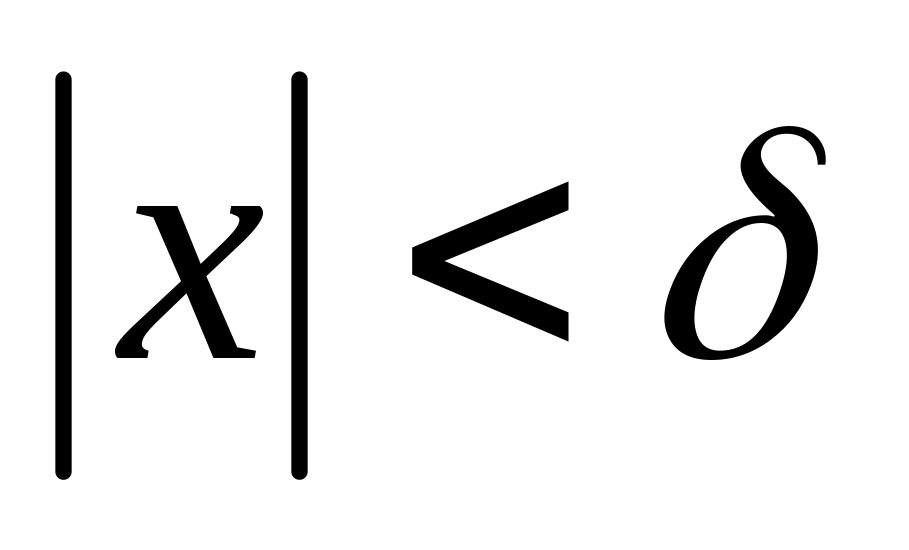2. Условие эквивалентно условию , следовательно , , т.к. .

3. Рассмотрим модуль .

.

Получили функцию .

4. Разрешим это неравенство относительно :

Таким образом, мы нашли , удовлетворяющее условиям определения непрерывности функции. Следовательно, данная функция непрерывна в точке .

2. Пользуясь определением доказать непрерывность функции

в точке .

Решение:

1) Зафиксируем

2) Используя , получаем оценку:

3) Находим зависимость от :

4) Определяем интервал значений :

.