Умения по теме т-10 “Предел и непрерывность функции нескольких переменных”
1. Изображение множеств на плоскости
1. Изобразить множество , если
,
,
,
.
Решение:
Построим поочередно множества
,
,
.
2.1. Определение типов точек
1. Пусть .
Какими будут являться точки:
, 
, 
, 
.
для множества
(внешними,
внутренними, предельными, граничными,
изолированными).
Решение:
а) Точка принадлежит множеству , причём существует окрестность этой точки входящая в множество , следовательно, точка является внутренней точкой множества . Каждая внутренняя точка множества является предельной, не является граничной и не является внешней точкой этого множества. Значит, точка − внутренняя, предельная точка множества .
Точка
не принадлежит множеству
,
причём существует окрестность этой
точки, в которой нет никакой точки
принадлежащей множеству
.
Значит, точка
− не предельная, не прикосновения, не
граничная. Точка
-
внешняя.
Точка не принадлежит множеству , но в любой окрестности этой точки находится точка, принадлежащая множеству . Значит, точка − предельная, не принадлежащая множеству , граничная точка.
Точка
принадлежит множеству
,
причём существует окрестность этой
точки не входящая в множество
никакой точкой кроме точки
,
следовательно, точка
является изолированной точкой множества
.
Следовательно она не может быть внутренней
или предельной
Ответ: − внутренняя, прикосновения, предельная точка, принадлежащая множеству ;
− внешняя для множества точка;
− граничная, прикосновения, предельная, не принадлежащая множеству точка;
- изолированная, прикосновения точка множества ;
2.2. Определение типов множеств
1. Пусть .
Определить, является ли множество ограниченным, неограниченным, открытым, замкнутым, связным.
Решение:
Рассмотрим, является ли множество
ограниченным. Существует двумерный куб
с центром в начале координат
такой, что
,
.
Следовательно, множество
− ограниченно.
Не каждая точка множества − внутренняя, следовательно, множество −не открытое.
Точки, лежащие на окружности
− точки прикосновения, они не принадлежат
множеству
,
значит множество
− незамкнутое.
Кроме того, очевидно, что не любые две точки этого множества можно соединить непрерывной кривой. Это происходит за счет существования изолированной точки. Следовательно, множество не связное.
Ответ: − ограниченное, не открытое, не замкнутое, не связное множество.
2. Является ли множество
областью.
Решение:
Для установления истинности утверждения построим данное множество на плоскости:
Точка (-2;2), очевидно, является граничной
для обоих множеств и не принадлежит ни
одному из них, а, следовательно, и
множеству
.
Таким образом, множество
состоит из двух отдельных открытых
множеств. Следовательно, оно не связанно
и не является областью.
Ответ: нет, не является.
3. Является ли область определения функции
областью?
Решение:
Найдем область определения данной функции:
.
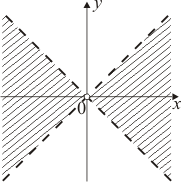
Следовательно, область определения данной функции – не связное множество, и оно не является областью.