,

Электрический заряд дискретен 1,6 10^-19 Кл.

Теории близкодействия взаимодействие между телами всегда осуществляется посредством тех или иных полей: гравитационное взаимодействие - посредством гравитационного поля, электромагнитное взаимодействие - посредством электромагнитного поля и т.д. Поле представляет собой особый вид материи. Оно характеризуется энергией, массой, импульсом и другими величинами.

Теорема Остроградского

Теорема Стокса

1. 

2)

3)

4)

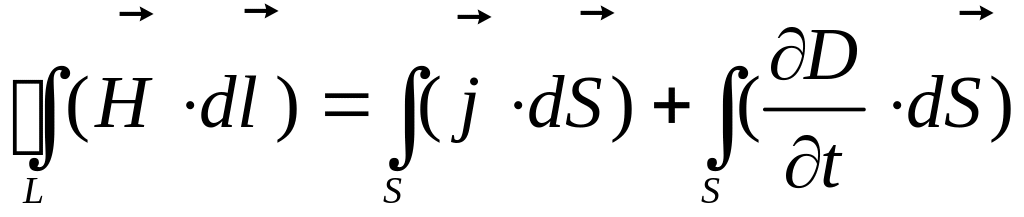
5)

6)

7)

Оператор Набла

ДИВЕРГЕНЦИЕЙ — (расхождение ) вектора называют предел отношения потока вектора через замкнутую поверхность к величине объем ограниченного этой поверхностью при условии, что объем стремится к нулю

Оператор Лапласа

Закон Кулона. Напряженность электрического поля.

Принцип суперпозиции электрических полей

Закон Кулона Франция 1785 г

Сила взаимодействия двух точечных зарядов прямо пропорциональна величине каждого из зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль линии соединяющей центры этих зарядов.

,

Здесь q₁ и q₂ – величины взаимодействующих зарядов;

r – расстояние между зарядами;

– единичный вектор, имеющий направление радиус-вектора заряда;

₀ = 8,8510^-12 Ф/м – электрическая постоянная.

Нм²/Кл²

Силовой характеристикой электрического поля служит векторная физическая величина , называемая напряженностью поля.

напряженности электрического поля это векторная физическая величина, равная отношению силы действующей на заряд к величине этого заряда, помещенного в данную точку поля.

Напряженность электрического поля точечного заряда q определяется формулой

.

Принцип суперпозиции

Если электрическое поле создано не одним, а несколькими зарядами, то напряженность результирующего поля будет равна векторной сумме напряженностей полей, созданным каждым зарядом в отдельности.

.

Работа электрического поля по перемещению электрического заряда.

Работа силы на элементарном перемещении равна

q_o – заряд, создающий электрическое поле;

q – заряд, перемещающийся в этом поле;

Потенциалом электрического поля называют скалярную величину, равную отношению потенциальной энергии которой обладает заряд, помещенный в данную точку поля к величине этого заряда.

.

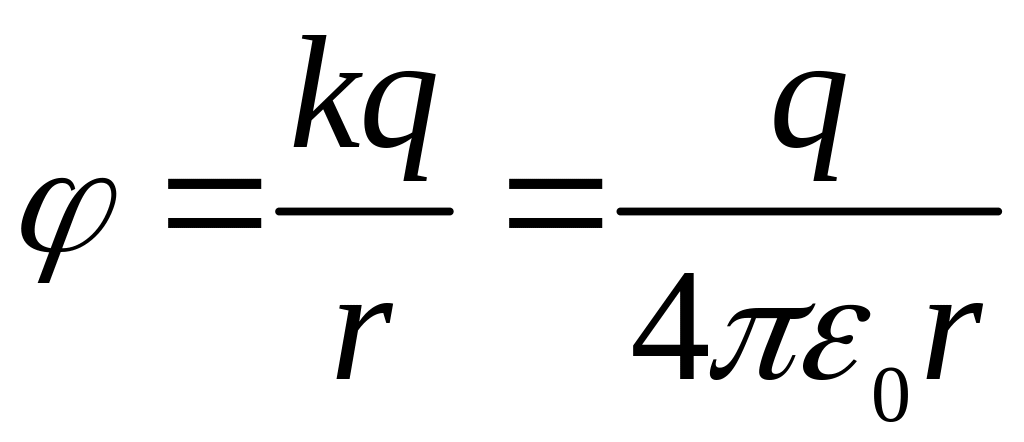Очевидно, если электрическое поле создается несколькими зарядами, то потенциал такого поля будет равен сумме потенциалов электрических полей каждого заряда в отдельности

. (1.13)

Принимая во внимание понятие потенциала электрического поля, для работы электрических сил из получим фундаментальное соотношение

.

Связь напряженности и потенциала

Иначе

,

.

.

Сравнивая, левые и правые части приведенной формулы, приходим к выводу о том, что:

.

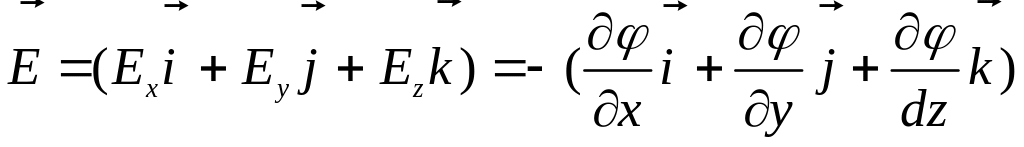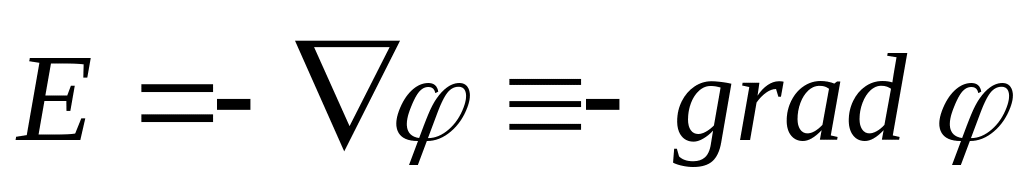
представляет собой вектор, направление которого совпадает с направлением быстрейшего возрастания потенциала. Знак «минус» указывает на то, что вектор напряженности электрического поля направлен в сторону убывания потенциала.

Поток вектора

Т еорема Остроградского- Гаусса

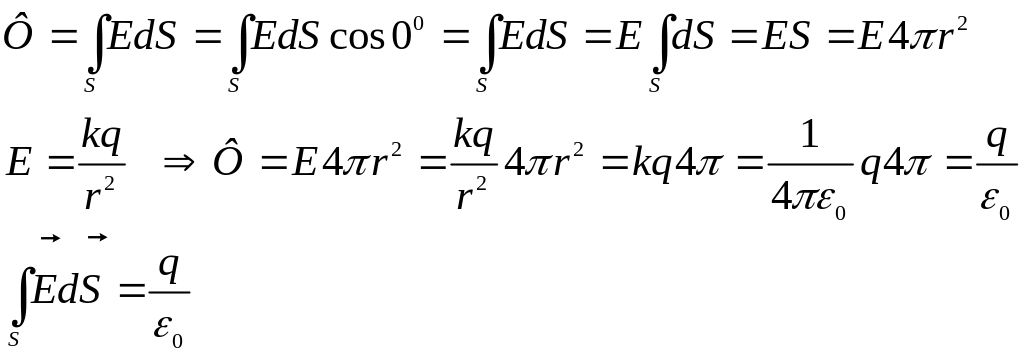
Плотность заряда :

линейная

поверхностная

обьемная

ПРИМЕНЕНИЕ ТЕОРЕМЫ ОСТРОГРАДСКОГО-ГАУССА ДЛЯ РАСЧЕТА ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ

Равномерно заряженная бесконечная плоскость

1.

C_n

2. Две равномерно заряженные плоскости.

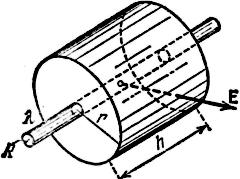
3. Равномерно заряженный бесконечный цилиндр.

Ф = Ф бок + 2 Ф осн = E Sбок cos 0` + 2 E (1) S осн cos90`= E 2 ПrL +0

E

r

R

4. Равномерно заряженный шар