1. Інформація. Сучасні теорії інформації. Класична теорія к.Шеннона. Інформація I повідомлення. Кодування інформації. Двiйковi знаки. Кількість інформації. Одиниці вимірювання інформації.

Інформація — це важлива наукова категорія, інтерес до якої не послаблюється з часом. Інформація (від лат. — informatio) — ознайомлення, роз’яснення, уявлення, поняття. У науці цей термін трактується як повідомлення, освідомлення про стан справ, повідомлення про що-небудь, що переказується людьми; невизначеність, яка зменшується або знімається внаслідок одержання повідомлень; повідомлення, що нерозривно пов’язано з управлінням; сигнали в єдності синтаксичних, семантичних і прагматичних характеристик; передача, відображення різноманіття в будь-яких об’єктах і процесах живої та неживої природи.

Сучасні теорії інформації:

• Імовірнісна теорія інформації;

• Алгоритмічна теорія інформації;

• Семантична теорія інформації.

Класична теорія інформації К.Шеннона

Аксіоми теорії інформації:

1. Інформація є лише там, де функціонують пристрої керування.

2. Інформація зберігається і передається тільки на матеріальному носії.

3. Інформація має ідеальний характер.

4. Інформація має різні форми.

Базові закони теорії інформації: 

Закон 1: на отримання інформації будь-яка кібернетична система витрачає не менше деякої мінімальної кількості енергії.

Закон 2: кількість інформації, яку отримує кібернетична система в процесі розпізнавання після прийняття певного сигналу, дорівнює логарифму при основі m від кількості варіантів вибору, що передували розпізнаванню.

Закон 3: що меншою є ймовірність завершення якогось випробування з певним результатом, то більше інформації для будь-якої кібернетичної системи несе саме цей результат, і навпаки.

Закон 4: будь-які сигнали, отримані кібернетичною системою, впливають на цю систему.

Будемо розрізняти поняття "інформація" і "повідомлення". Під повідомленням розуміють звичайно інформацію, виражену у визначеній формі та таку, що підлягає передачі. Повідомлення - це форма подання інформації. Прикладами повідомлень є текст телеграми, промова оратора, показання вимірювального приладу, команди керування, зображення на екрані телевізора та ін.

Кодування являє собою перехід від повідомлення на вході каналу зв'язку до коду повідомлення на виході, а декодування - зворотний процес переходу від коду повідомлення на виході каналу зв'язку до повідомлення на вході, при цьому повідомлення на вході й виході з каналу зв'язку повинні збігатися.

Більш суворо задачу кодування можна сформулювати в такий спосіб. Нехай є два алфавіти: алфавіт А, що складається з  n  символів і алфавіт B, що складається з m символів. Під алфавітним кодуванням розуміють таке відображення F, яке кожному слову з непустої підмножини слів з алфавіту A ставить у відповідність деяке слово з алфавіту B. Слова з алфавіту B називаються кодовими послідовностями або кодами. Традиційно, відображення F задається у вигляді деякого алгоритму й повинне задовольняти наступним вимогам:

• взаємна однозначність, тобто можливість для кожного повідомлення однозначно побудувати його код і, обернено, по кожному коду однозначно відновити вихідне повідомлення;

• завадостійкість, тобто можливість виявляти і виправляти помилки, які можуть виникнути при передачі коду повідомлення по каналу зв'язку під впливом джерела шуму;

• економність, тобто можливість побудови кодів мінімальної довжини для повідомлень, що зустрічаються найчастіше (реалізація ефективного стиснення).

Побудова ефективного алгоритму кодування – це пошук компромісу між другою і третьою вимогами, які суперечать одна одній, оскільки завадостійкість досягається за рахунок збільшення довжини кодових послідовностей.

Двійкова система забезпечує ефективний спосіб представлення чисел.

Двійкова система незручна для візуальної індикації та реєстрації, проте обчислювальні пристрої і дискретні перетворювачі, що працюють за двійковою системі, побудовані на більш надійних і простих елементах, що мають тільки два добре помітних стану.

Двійкова система, виявляється, особливо зручна для розрахунків на електронно-обчислювальних машинах, з якими її онуки працюють.

Двійкова система використовує тільки дві цифри, 0 і 1 і тому є найбільш придатною для перемикаючих схем. Правила додавання, віднімання, ділення і множення для двійкової та десяткової системи однакові. Хоча для вираження числа в двійковій системі буде потрібно більше цифр, ніж у десятковій системі, простота, з якою електронна схема може звертатися з двійковим поданням числа, призвела до майже винятковому використанню двійкової системи.

Кількість інформації

Ентропійний підхід

В основі теорії інформації лежить запропонований Шенноном спосіб обчислення кількості інформації як випадкової величини відносно іншої випадкової величини. Для дискретних випадкових величин X і Y, заданих законами розподілу   і спільним законом розподілу  , кількість інформації в X відносно Y, дорівнює

Кількість інформації в повідомленні визначається тим, наскільки зменшиться невизначеність після одержання повідомлення. З цього погляду, кількість інформації, що міститься в отриманому повідомленні тим більше, чим більше була невизначеність до передачі повідомлення.

Об'ємний підхід

Під обсягом інформації в повідомленні мають на увазі кількість символів цього повідомлення. Обсяг інформації – це досить груба кількісна характеристика інформації, оскільки суттєво залежить від форми подання інформації.

Алгоритмічний підхід

Згідно з алгоритмічним підходом за кількість інформації приймається значення деякої функції від складності кожного з об'єктів і довжини програми (алгоритму) перетворення одного об'єкта в іншій. Інтуїтивно зрозуміло, що комп'ютерна програма, яка друкує повідомлення, що містить тільки нулі, украй проста. Усе, що потрібно робити цій програмі, – це друкувати один і той самий символ – нуль. Якщо ж повідомлення являє собою деяку послідовність, яка не підпорядковується ніяким закономірностям, то таке повідомлення не може бути реалізоване жодною «простою» програмою. У цьому випадку, довжина програми буде близька до довжини самої послідовності. Таким чином, кількість інформації в повідомленні визначається складністю програми, яка здатна відтворити це повідомлення – послідовність символів.

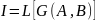
A – вхідний об'єкт; B – вихідний об'єкт; G – програма перетворення; L – функція отримання довжини програми (в бітах чи байтах).

Одиниці виміру інформації служать для вимірювання об'єму інформації - величини, що обчислюється логарифмічно. Це означає, що коли кілька об'єктів розглядаються як один, кількість можливих станів перемножується, а кількість інформації - складається. Не важливо, йде мова про випадкових величинах в математиці, регістрах цифрової пам'яті в техніці або в квантових системах у фізиці.

Найчастіше вимір інформації стосується обсягу комп'ютерної пам'яті та обсягу даних, переданих по цифрових каналах зв'язку.

Цілі кількості біт відповідають кількості станів, рівному ступенями двійки.

Особливу назву має 4 біта - ніббл (напів байт, тетрада, чотири двійкових розряди), які вміщують в себе кількість інформації, що міститься в одній шістнадцятковій цифрі.

Наступною по порядку популярної одиницею інформації є 8 біт, або байт. Саме до байту безпосередньо наводяться всі великі обсяги інформації, які обчислюються в комп'ютерних технологіях.

Такі величини як машинне слово і т. п., складові кілька байт, як одиниці вимірювання майже ніколи не використовуються.

Для вимірювання великих кількостей байтів служать одиниці "кілобайт" = [1024] байт і "Кбайт" (кібібайт, kibibyte) = 1024 байт. Такий порядок величин мають, наприклад:

• Сектор диска зазвичай дорівнює 512 байтам тобто половині кілобайти, хоча для деяких пристроїв може дорівнювати одному або двом кібібайт.

• Класичний розмір "блоку" у файлових системах UNIX дорівнює одному Кбайт (1024 байт).

• "Сторінка пам'яті" в процесорах x86 (починаючи з моделі Intel 80386) має розмір 4096 байт, тобто 4 Кбайт.

Обсяг інформації, що отримується при зчитуванні дискети "3,5" високої щільності "дорівнює 1440 Кбайт (рівно), інші формати також обчислюються цілим числом Кбайт.

Одиниці "мегабайт" = 1024 кілобайт = [1048576] байт і "Мбайт" (мебібайт, mebibyte) = 1024 Кбайт = 1048576 байт застосовуються для вимірювання обсягів носіїв інформації.

Обсяг адресного простору процесора Intel 8086 був дорівнює 1 Мбайт.

Оперативну пам'ять і ємність CD-ROM міряють двійковими одиницями (мебібайтамі, хоча їх так зазвичай не називають), але для обсягу НЖМД десяткові мегабайти були більш популярні.

Сучасні жорсткі диски мають обсяги, висловлені в цих одиницях мінімум шестизначними числами, тому для них застосовуються гігабайти.

Одиниці "гігабайт" = 1024 мегабайт = [1048576] кілобайт = [1073741824] байт і "Гбайт" (гібібайт, gibibyte) = 1024 Мбайт = 2 ³⁰ байт вимірюють обсяг великих носіїв інформації, наприклад жорстких дисків. Різниця між двійкової та десяткової одиницями вже перевищує 7%.

Розмір 32-бітного адресного простору дорівнює 4 Гбайт ≈ 4,295 Мбайт. Такий же порядок мають розмір DVD-ROM і сучасних носіїв на флеш-пам'яті. Розміри жорстких дисків вже сягають сотень і тисяч гігабайт.

Для обчислення ще більших обсягів інформації є одиниці терабайт і тебібайт (10 ¹² і 2 ⁴⁰ байт відповідно), петабайт і пебібайт (10 ¹⁵ і 2 ⁵⁰ байт відповідно) і т. д.