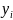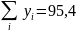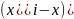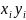Лекция №8

Тема 6. «Применение экономико-математических методов в решении типовых аналитических задач»

Вопрос 1. Метод корреляционно-регрессионного анализа.

Вопрос 2. Методы линейного программирования.

Вопрос 1. Метод корреляционно-регрессионного анализа

Метод корреляционного и регрессионного анализа широко ис­пользуется для определения тесноты связи между показателями, не находящимися в функциональной зависимости. Теснота связи между изучаемыми явлениями измеряется корреляционным от­ношением (для криволинейной зависимости). Для прямолиней­ной зависимости исчисляется коэффициент корреляции.

Одной из распространенных аналитических задач, решае­мых с применением корреляционно-регрессионного метода, является задача на запуск — выпуск. Допустим, что имеются фактические данные о запуске и выпуске промышленных изде­лий (табл. 10).

Требуется определить зависимость выпуска изделий в сред­нем от их запуска, составив соответствующее уравнение рег­рессии.

Таблица 10 - Фактические данные о запуске – выпуске промышленных изделий, тыс. шт.

Запуск	18	22	13	20	15	14
Выпуск	17,2	20,9	11,6	18,7	14,1	12,9

Значения x и y определяются по формулам:

; ; n=6, i=1,.,6;

; .

Дальнейшим вычислениям придается табличная форма, что повышает их наглядность (табл. 11).

1	1	1,3	1,69	1,3
5	25	5	25	25
-4	16	-4,3	18,49	17,2
3	9	2,8	7,84	8,4
-2	4	-1,8	3,24	3,6
-3	9	-3	9	9

Теснота связи между показателями запуска и выпуска измеря­ется коэффициентом корреляции, который исчисляется по формуле:

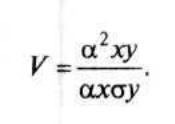
Подставляя соответствующие значения, получим:

Считая формулу связи линейной 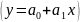,определим за­висимость выпуска промышленных изделий от их запуска. Для этого решается система нормальных уравнений

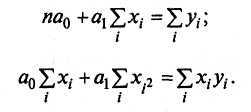
Величины и представлены в следующей таблице (табл. 12).

Таблица 12

	324	484	169	400	225	196
	309,6	459,8	150,8	374,0	211,5	180,6

Значение определяем из первого уравнения:

;

;

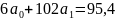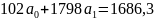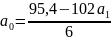, или

Подставляя найденное выражение во второе уравнение, находим значение :

;

;

;

; ;

; ;

.

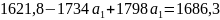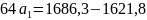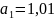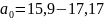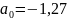Итак, уравнение регрессии в окончательном виде получило следующий вид:

.

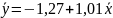Проверка:

;

.

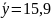Вопрос 2. Методы линейного программирования

Методы линейного программирования применяются для реше­ния многих экстремальных задач, с которыми довольно часто приходится иметь дело в экономике. Решение таких задач сво­дится к нахождению крайних значений (максимума и минимума) некоторых функций переменных величин.

Линейное программирование основано на решении системы линейных уравнений (с преобразованием в уравнения и неравен­ства), когда зависимость между изучаемыми явлениями строго функциональна. Для него характерны математическое выраже­ние переменных величин, определенный порядок, последова­тельность расчетов (алгоритм), логический анализ. Применять его можно только в тех случаях, когда изучаемые переменные ве­личины и факторы имеют математическую определенность и ко­личественную ограниченность, когда в результате известной пос­ледовательности расчетов происходит взаимозаменяемость фак­торов, когда логика в расчетах, математическая логика совмеща­ются с логически обоснованным пониманием сущности изучае­мого явления.

С помощью этого метода в промышленном производстве, нап­ример, исчисляется оптимальная общая производительность ма­шин, агрегатов, поточных линий (при заданном ассортименте про­дукции и иных заданных величинах), решается задача рациональ­ного раскроя материалов (с оптимальным выходом заготовок). В сельском хозяйстве он используется для определения минималь­ной стоимости кормовых рационов при заданном количестве кор­мов (по видам и содержащимся в них питательным веществам). За­дача о смесях может найти применение и в литейном производстве (состав металлургической шихты). Этим же методом решаются транспортная задача, задача рационального прикрепления предп­риятий-потребителей к предприятиям-производителям.

Все экономические задачи, решаемые с применением линей­ного программирования, отличаются альтернативностью реше­ния и определенными ограничивающими условиями. Решить такую задачу — значит выбрать из всех допустимо возможных (альтернативных) вариантов лучший, оптимальный. Важность и ценность использования в экономике метода линейного прог­раммирования состоят в том, что оптимальный вариант выбира­ется из весьма значительного количества альтернативных вари­антов. При помощи других способов решать такие задачи практи­чески невозможно.

Весьма типичной задачей, решаемой с помощью линейного программирования, является транспортная задача. Ее смысл зак­лючается в минимизации грузооборота при доставке товаров ши­рокого потребления от производителя к потребителю, с оптовых складов и баз в розничные торговые предприятия. Она решается симплекс-методом или распределительным методом.