Вопрос 1.1. Типы факторных систем в детерминированном моделировании.

Одной из задач факторного анализа является моделирование взаимосвязей между результативными показателями и факторами, которые определяют их величину.

Моделирование – это один из важнейших методов научного познания, с помощью которого создается модель (условный образ) объекта исследования. Сущность моделирования заклю­чается в том, что взаимосвязь исследуемого показателя с факторными выражается в форме конкретного математического уравнения.

В факторном анализе различают модели детерминированные (функциональные) и стохастические (корреляционные). С помощью детерминированных факторных моделей исследуется функциональная связь между результативным показателем (функцией) и факторами (аргументами).

При создании детерминированных факторных моделей необходимо выполнять ряд требований:

1. Факторы, включаемые в модель, должны реально существовать, а не быть надуманными абстрактными величинами или явлениями;

2. Факторы, входящие в модель, должны находиться в причинно-следственной взаимосвязи с изучаемым показателем;

3. Все показатели факторной модели должны быть количественно измеримыми, т.е. иметь единицу измерения и необходимую информационную базу;

4. Факторная модель должна обеспечивать возможность измерения влияния отдельных факторов, т.е. в ней должна учитываться соразмерность измерений результативного и факторных показателей, а сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.

В детерминированном анализе выделяют следующие типы наи­более часто встречающихся факторных моделей.

1. Аддитивные модели:

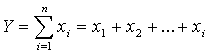
Они используются в тех случаях, когда результативный показа­тель представляет собой алгебраическую сумму нескольких фак­торных показателей.

2. Мультипликативные модели:

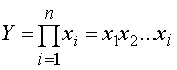
Этот тип моделей применяется тогда, когда результативный по­казатель представляет собой произведение нескольких факторов.

3. Кратные модели:

Они используются тогда, когда результативный показатель по­лучают делением одного факторного показателя на величину дру­гого.

4. Смешанные (комбинированные) модели — это сочетание в различных комбинациях предыдущих моделей:

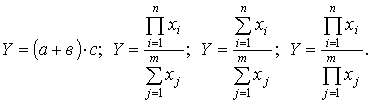
Процесс моделирования факторных систем — очень сложный и ответственный момент в АХД. От того, насколько реально и точ­но созданные модели отражают связь между исследуемыми пока­зателями, зависят конечные результаты анализа.

Вопрос 1.2 Метод цепных подстановок.

Способ цепных подстановок заключается в определении ряда промежуточных значений обобщающего показателя путем последовательной замены базисных значений факторов на отчетные. Данный способ основан на элиминировании. Элиминировать – значит устранить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. При этом исходя из того, что все факторы изменяются независимо друг от друга, т.е. сначала изменяется один фактор, а все остальные остаются без изменения. потом изменяются два при неизменности остальных и т.д.

Он используется для расчета влияния факторов во всех типах де­терминированных факторных моделей: аддитивных, мультиплика­тивных, кратных и смешанных (комбинированных). Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме резуль­тативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных значений результативного показа­теля, которые учитывают изменение одного, затем двух, трех и по­следующих факторов, допуская, что остальные не меняются. Срав­нение значений результативного показателя до и после изменения уровня того или другого фактора позволяет элиминировать влияние всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя.

В общем виде применение способа цепных постановок можно описать следующим образом:

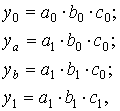
где a₀, b_0, c₀ - базисные значения факторов, оказывающих влияние на обобщающий показатель у_;

a₁ , b₁, c₁ - фактические значения факторов;

y_a, y_b, - промежуточные изменения результирующего показателя, связанного с изменением факторов а, b, соответственно.

Общее изменение складывается из суммы изменений результирующего показателя за счет изменения каждого фактора при фиксированных значениях остальных факторов:

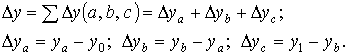
Рассмотрим пример:

Таблица 6 - Исходные данные для факторного анализа

Показатели	Условные обозначения	Базисные значения (0)	Фактические значения (1)	Изменение
				Абсолютное (+,- )	Относительное (%)
Объем товарной продукции, тыс. руб.	ТП	2920	3400	+480	116,40
Количество работников, чел	Ч	20	25	+5	125,00
Выработка на одного работающего, тыс. руб.	СВ	146	136	-10	93,15

Анализ влияния на объем товарной продукции количества работников и их выработки проведем описанным выше способом на основе данных Таблицы 6. Зависимость объема товарной продукции от данных факторов можно описать с помощью мультипликативной модели:

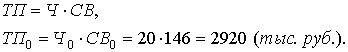
Тогда влияние изменения величины количества работников на обобщающий показатель можно рассчитать по формуле:

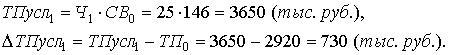
Далее определим влияние изменения выработки работников на обобщающий  показатель

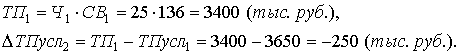
Таким образом, на изменение объема товарной продукции положительное влияние оказало изменение на 5 человек численности работников, что вызвало увеличение объема продукции на 730 тыс. руб. и отрицательное влияние оказало снижение выработки на 10 тыс. руб., что вызвало снижение объема на 250 тыс. руб. Суммарное влияние двух факторов привело к увеличению объема продукции на 480 тыс. руб.

В кратных моделях алгоритм расчета факторов на величину исследуемых показателей следующий:

; ; .

Общее изменение уровня фондоотдачи:

.

В том числе за счет:

- объема производства продукции:

;

- суммы основных производственных фондов:

,

Где ФО – фондоотдача;

ОПФ – среднегодовая стоимость основных производственных фондов.

Отдельно необходимо остановиться на методике определения влияния структурного фактора с помощью способа цепной под­становки. Методику этого расчета рассмотрим на примере вы­ручки от реализации продукции (В), которая во многом зависит не только от цены (Ц) и количества проданной продукции (VPП), но и от ее структуры ( ). Если возрастет доля продук­ции высшей категории качества, которая продается по более вы­соким ценам, то выручка за счет этого увеличится, и наоборот. Факторная модель этого показателя может быть записана так:

.

В процессе анализа необходимо элиминироваться от воздей­ствия всех факторов, кроме структуры продукции. Для этого сравниваем следующие показатели выручки:

Разность между этими показателями учитывает изменение выручки только за счет изменения структуры или сортового со­става продукции (табл. 7).

Из таблицы видно, что с увеличением удельного веса про­дукции второго сорта в общем объеме ее реализации выручка уменьшилась на 10 млн руб. (655 – 665). Это можно расценивать как неиспользованный резерв предприятия.

Таблица 7 - Расчет влияния структурного фактора на изменение выручки от реализации продукции способом цепной подстановки

Сорт продукции	Цена 1 т, тыс. руб.	Объем продаж, т		Структура продаж		Объем продаж отчетного периода при базисной его структуре, т	Выручка в млн руб. за при структуре
1-й	2700	180	200	0,9	0,8	225	607,5	540
2-й	2300	20	50	0,1	0,2	25	57,5	115
Итого		200	250	1,0	1,0	250	655,0	655

Используя способ цепной подстановки, необходимо знать правила последовательности расчетов: в первую очередь нужно учитывать изменение количественных, а затем качественных показателей. Если же имеется несколько количественных и несколько каче­ственных показателей, то сначала следует изменить величину фак­торов первого порядка, а потом более низкого.

Преимущества данного способа: универсальность применения, простота расчетов.

Недостаток метода состоит в том, что, в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения. Это связано с тем, что в результате применения этого метода образуется некий неразложимый остаток, который прибавляется к величине влияния последнего фактора. На практике точностью оценки факторов пренебрегают, выдвигая на первый план относительную значимость влияния того или иного фактора. Однако существуют определенные правила, определяющие последовательность подстановки: · при наличии в факторной модели количественных и качественных показателей в первую очередь рассматривается изменение количественных факторов; · если модель представлена несколькими количественными и качественными показателями, последовательность подстановки определяется путем логического анализа.

Под количественным факторами при анализе понимают те, которые выражают количественную определенность явлений и могут быть получены путем непосредственного учета (количество рабочих, станков, сырья и т.д.).

Качественные факторы определяют внутренние качества, признаки и особенности изучаемых явлений (производительность труда, качество продукции, средняя продолжительность рабочего дня и т.д.).