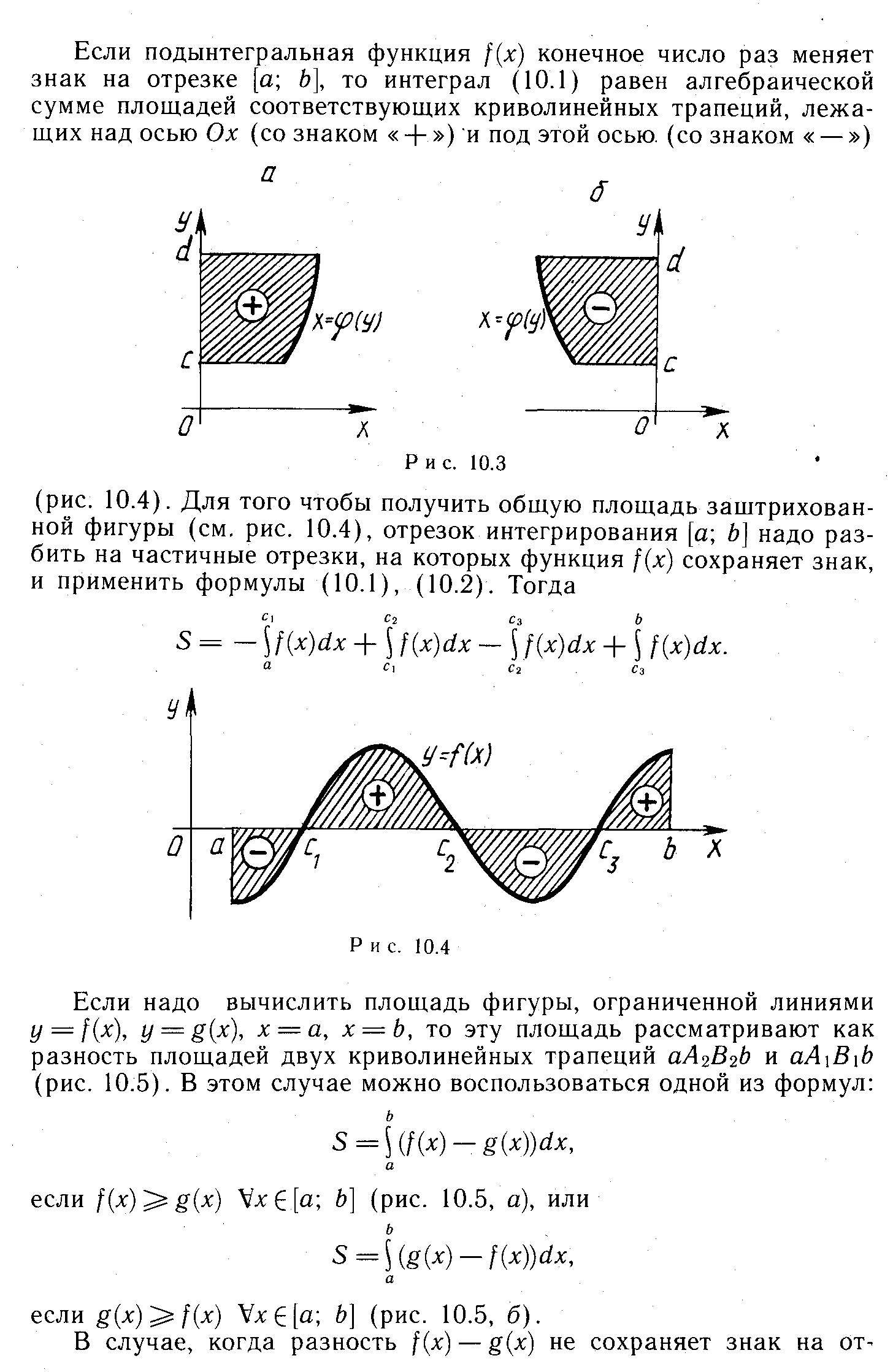
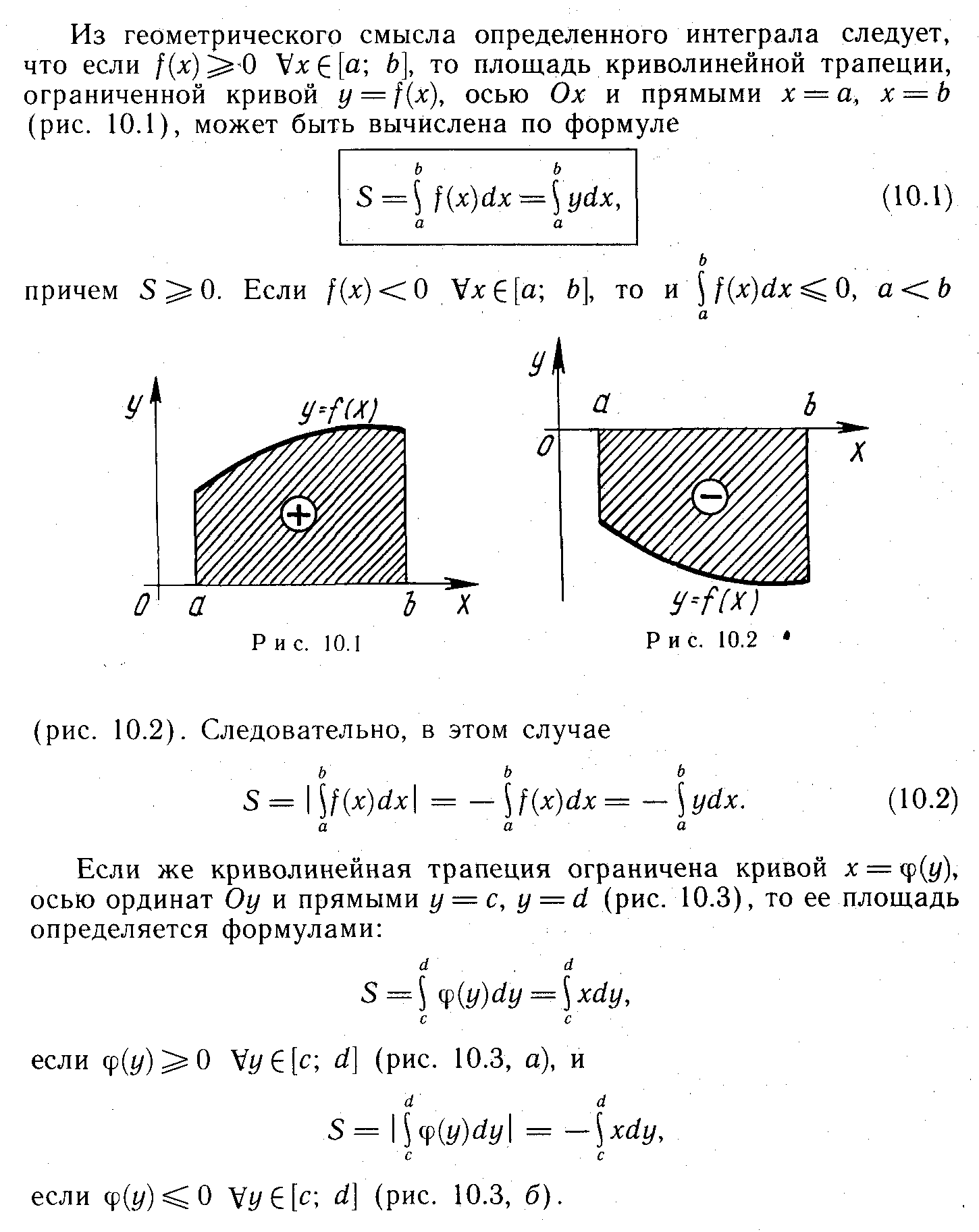- •1. Функция
- •2. Дифференцируемость ф-ии. Теорема о непрерывности диф-мой ф-ции
- •3. Т. Коши об обращ. В нуль ф-ии, непрер. На отрезке.
- •4.Т.Веерштрасса. Св-ва ф-ии непрер на отр-ке.
- •5.Мощность мн-ва.
- •6. Предел функции.Теорема о пределе суммы, произведения и частного двух функций.
- •7. Посл-ти. Св-во. Т о единств. Предела посл-ти.
- •8. Теоремы Лагранжа, Роля и Ферма о дифференцируемых функциях.
- •9. Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
- •10. Производная в с. Условия ее сущ. Аналитич-ие ф-ии. Их свойства.
- •11. Теорема о существовании предела у монотонной ограниченной последовательности.
- •12. Степень в компл. Обл-ти.
- •13. Определенный интеграл.
- •14. Теорема о существовании точных границ у ограниченного мн-ва.
- •15. Лду 2 порядка с постоянными коэффициентами.
- •16. Двойной интеграл и его применение.
- •17. Числовые ряды. Признак Даламбера сходимости положительных числовых рядов.
- •18 Ряд Тейлора.
- •19. Определение и вычисление длины дуги.
- •20. Функции двух переменных. Дифференцируемость функции двух переменных.
- •21. Дифференциальные уравнения I-го порядка
- •22. Непрерывность функции.
- •23.Производнвя функции действительного переменного. Теорема о производной суммы, произведения и частного двух функций.
- •25. Квадрируемые фигуры. Вычисление площадей.
18 Ряд Тейлора.

19. Определение и вычисление длины дуги.
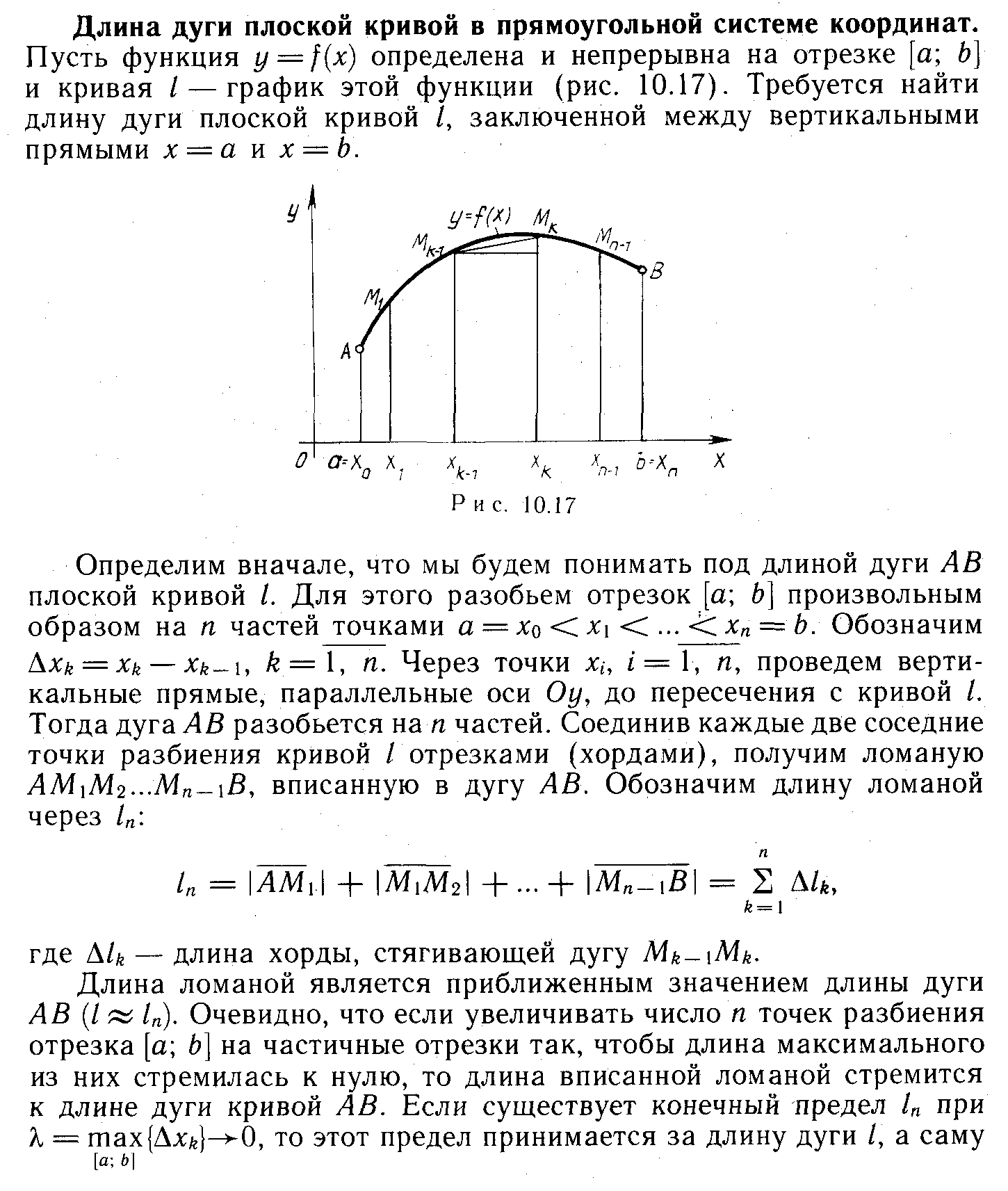

Если линия задана
параметрически:
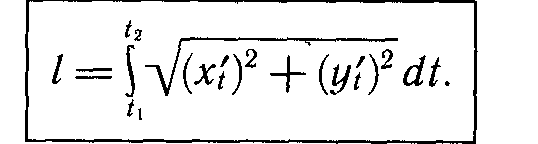
Если линия задана
в полярных коор-тах:
20. Функции двух переменных. Дифференцируемость функции двух переменных.
Если любой паре упорядоченных чисел (x, y) из некоторого множества D
поставлено в соответствие единственное число z, то переменная z называется
функцией двух переменных.
z = f (x, y)
Переменную z называют зависимой переменной, а переменные x и y –
независимыми. Множество D называется областью определения функции, а
множество z – множеством значений функции.


Теорема2. Пусть у функции u = f(x1,x2,…,xn) в некоторой окрестности точки М существуют частные производные по всем аргументам, непрерывные в точке М. Тогда функция u = f(x1,x2,…,xn) дифференцируема в точке М.
21. Дифференциальные уравнения I-го порядка

22. Непрерывность функции.


23.Производнвя функции действительного переменного. Теорема о производной суммы, произведения и частного двух функций.



24.Исследование функции с помощью дифференциального исчисления. Пример: y=x2/(2x+1).
Пусть кривая задана уравнением y = f(x) в явном виде. Наглядное пред-
ставление об изучаемой функции да¨ет е¨е график.
Чтобы построить кривую по е¨е уравнению y = f(x), нужно провести ис-
следование, выявляющее существенные качества этой кривой (функции). При-
вед¨ем схему исследования функции y = f(x) для построения е¨е графика:
1. Определить область существования функции y = f(x).
2. Найти точки пересечения кривой y = f(x) с осями координат.
3. Определить симметрию функции относительно осей и начала координат (ис-
следовать на ч¨етность и неч¨етность).
4. Найти участки возрастания и убывания функции y = f(x).
5. Исследовать функцию на экстремум (найти вершины кривой).
6. Исследовать функцию на выпуклость, вогнутость и точки перегиба.
7. Найти асимптоты кривой.
8. По полученным данным построить график.
9. Иногда для более точного построения кривой полезно найти е¨е значения в
дополнительных точках.
25. Квадрируемые фигуры. Вычисление площадей.
Требуется вычислить площадь S(X). Площадь можно вычислять если она квадрируема (если предел сумм разбиения существует и единственный) S1S2...Sn S=(a...b)Sf(x)dx 1)Посл-ть сумм Sk –монотонно возрастает. 2) Sn – ограничена сверху sup Sn=Sx=limSn 3) Если X – неограничено, то limSn=+бескон., но не обязательно.