15. Лду 2 порядка с постоянными коэффициентами.

Здесь и далее n=2.

Для решения таких Ур-й исп-ся м-д вариации произвольной постоянной (м-д Лагранжа), разберем его на таком примере:

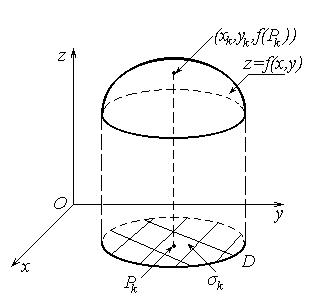
16. Двойной интеграл и его применение.

Двойной интеграл. Пусть функция z = f(x,y) определена в ограниченной замкнутой области D плоскости R2. Разобьём область D произвольным  образом на  n  элементарных замкнутых областей  1, … ,n, имеющих площади 1, …, n и диаметры d1 , …, dnсоответственно. Обозначим d наибольший из диаметров областей 1, … ,n . Диаметром замкнутой ограниченной области  называется наибольшее из расстояний между двумя точками границы этой области. В каждой области k выберем произвольную точку Pk (xk ,yk) и составим интегральную сумму функции f(x,y)    S  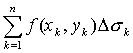=   (рис. 1).

Рисунок 1

Определение. Двойным интегралом функции f(x,y) по области D называется предел интегральной суммы

               ,

если он существует.

Двойной интеграл обозначается

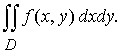       (1)

 Замечание. Интегральная сумма S зависит от способа разбиения области D и выбора точек Pk (k=1, …, n). Однако, предел  , если он существует, не зависит от способа разбиения области D и выбора точек Pk .

2. Достаточное условие существования двойного интеграла. Двойной интеграл (1) существует, если функция f(x,y) непрерывна в D за исключением конечного числа кусочно-гладких кривых и ограничена в D.

Некоторые свойства двойного интеграла.

1)      Линейность. Если С – числовая константа, то

,

.

2)      Аддитивность. Если область D  “разбита” на области D1 и D2, то

Применение в геометрии

1. Площадь ограниченной замкнутой области D в плоскости Oxy: 

2. Объем цилиндрического тела (образующие параллельны оси Oz), ограниченного снизу областью D плоскости Oxy, а сверху поверхностью 

3. Если участок поверхности, заданной уравнением   проектируется в область D на плоскости Oxy, причем функции   непрерывны в этой области, то площадь данного участка поверхности:

Применение в механике Пусть на плоскости Oxy находится материальная пластина, имеющая форму ограниченной замкнутой области D, причем в каждой точке данной области плотность определяется непрерывной функцией  1. Масса пластины:  2. Статические моменты пластины относительно осей Ox и Oy:

3. Координаты центра тяжести 

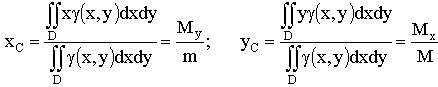
4. Моменты инерции пластины относительно осей Ox, Oy и начала координат:

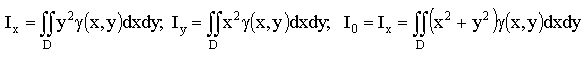
17. Числовые ряды. Признак Даламбера сходимости положительных числовых рядов.

Опр1. Пусть a1, a2, a3 .. an 0 некоторая посл-ть действ. чисел. Составл-ая из этих чисел формальная сумма a1+a2+a3+...+an+... наз-ся числов. рядом. Сокращ. (от 1 до бескон.)an. an - n-ый член ряда. Sn – n-ая частич. сумма.

Опр2. Если сущ конечный или бескон-ый предел S=Lim Sn (n8) то он наз-ся суммой ряда.

Опр3. Если ряд имеет конечную сумму, его наз-ют сход-ся, а в противном же случае – расход-ся.