9. Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.

Пусть на [a;b] задана интегр. ф-ия y=f(x). Возьмём .

Такой интегр. наз. интегр.с перемен.верхн.приделом.

Св-ва:

1) если y=f(x) интегр-ма на [a;b], то явл. непрер. ф-ей.

2) Если ф-ия y=f(x) непрер. на [a;b], то интеграл с переем. верхн. приделом явл. диф-ой ф-ей, причём произв. этой ф-ии будет равна подинтегр. ф-ии выч. в т. верхн. придела.

3) Если ф-ия y=f(x) непрер. на [a;b], то у неё на этом отр. сущ. первообразные, одной из первообр. для ф-ии y=f(x) явл. интеграл с перемен. верхн. приделом.

Ф-ла Ньютона-Лейбница: Если ф-ия y=f(x) непрер. на [a;b] и Ф(x) первообразная для этой фии на [a;b], то

Д-во: Т.к. y=(x) непрер. на [a;b] по 3) у неё сущ. первообр. и любую первообр. можно записать Ф(x)= . Пусть x=a, тогда Ф(a)=

10. Производная в с. Условия ее сущ. Аналитич-ие ф-ии. Их свойства.

Изобразим геомет. z и f(z) относ. точки z₀ для ф-ии w = f(z). z=х+iу. f(z) = u+ iν

Опр lim отнош. limf(z)/ z при z→0, если он сущесвует наз. производной ф-ий f(z₀) и обоз.d[f(z)]/dz или w'(z).Если ф-я имеет произв. в точке z₀ то говорят , что она диф-ма в этой точке (моногенной).Если ф-я имеет произ. в каждой точке обл., то её наз диф-ой или моногенной в этой области. Произв. это число.

Опр. Пусть f(z) – задана в нек. области E тогда lim(f(z)-f(z₀))/z-z₀ zz₀ – производная в точке z₀. Если он сущ-ет то производная в точке z₀ – обознач-ся f’(z₀)df(z₀)/dz. f(z) – наз-ют диф-ой в точке z₀ и в некоторой ее окр-ти то ф-ию наз-ют аналитич-ой в точке z₀. Критерий диф-ти для диф-ти ф-ии f(z) в точке z0 НиД чтобы f(z)=Az+E(z)z. E(z)- бескон малая относ-но z.

11. Теорема о существовании предела у монотонной ограниченной последовательности.

12. Степень в компл. Обл-ти.

zⁿ=Rⁿ(cos(nf)+isin(nf))

Отображение W=z^a, z Если n=1, то w=z-тождеств.отобр. . Ф-ия диф-ма в т. наз. целой. w(0)= ; w( .

Св-ва:

1) Ф-ия ;

2) Областью знач. ф-ии явл. Также вся расшир.компл. пл-ть;

Д-во: Если рассм. компл.число вида , k=0,…,n-1. Мы получ, что каждое из таких чисел будет иметь образ один и тот же. Д-но.

3) Отобр явл конформным во всех т. компл. пл-ти за искл. 0.

4) Argw= =nArgz(…); w= .

5) При отобр. каждая т. w имеет n разных прообразов в пл-ти z, которые содержатся в ф-ле , k=0,…,n-1; w=

6) При отобр. каждая окружн. С центром в 0 в пл-ти Z перейдёт в окр. с центрм в 0 и радиус котор. будет в n раз больше. При однокр. обходе пл-ти Z окр. в пл-ти W будет n-кратно обходиться в полож. напр.

7) Отобр. не облад. Св-вом взаимной однозначности.

13. Определенный интеграл.

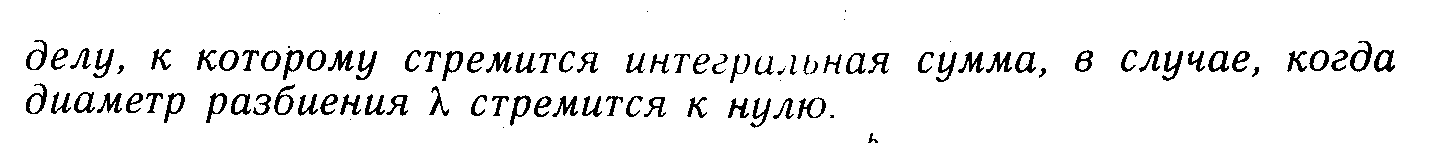
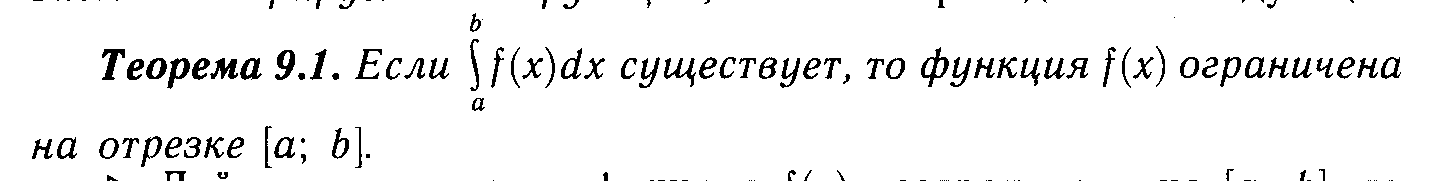
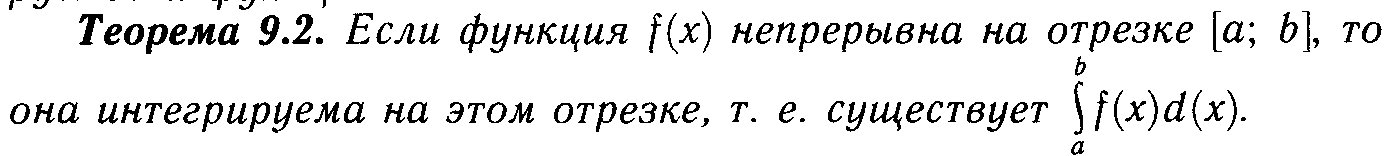
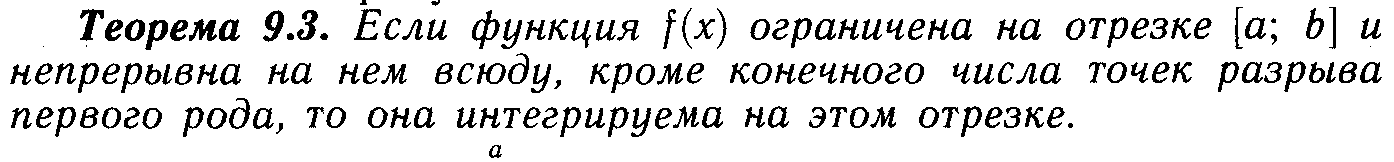
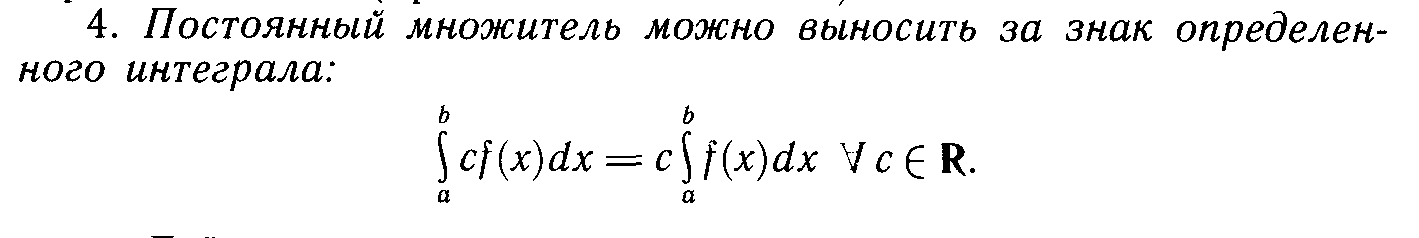
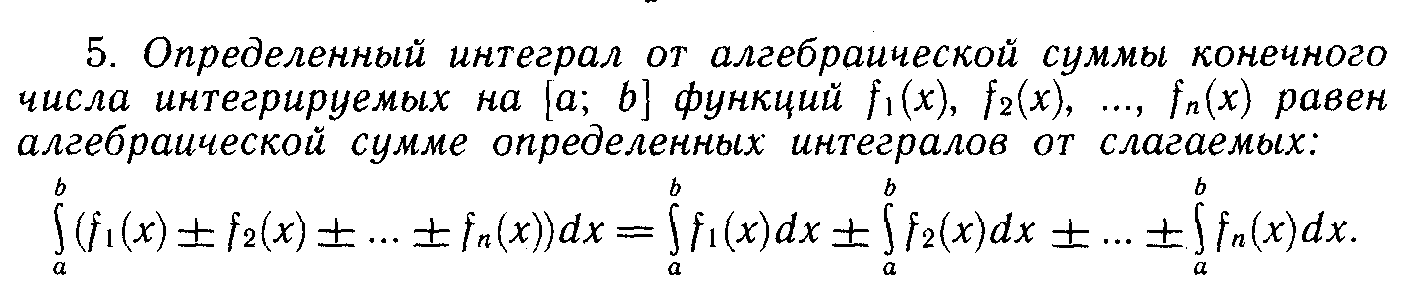
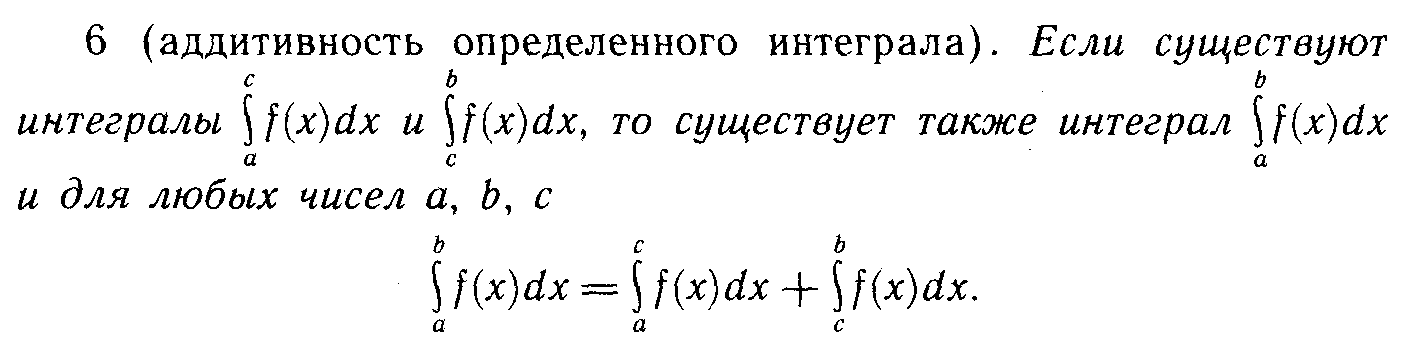
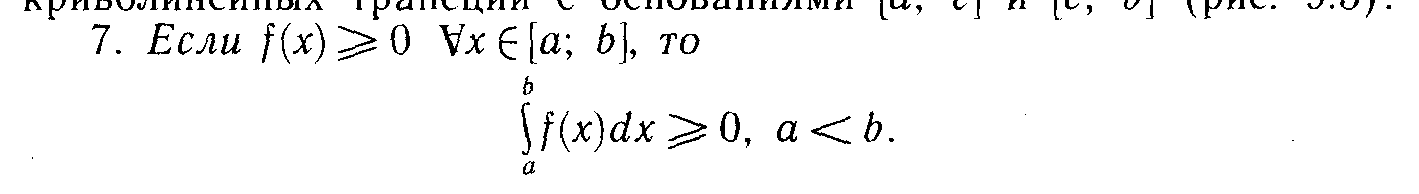
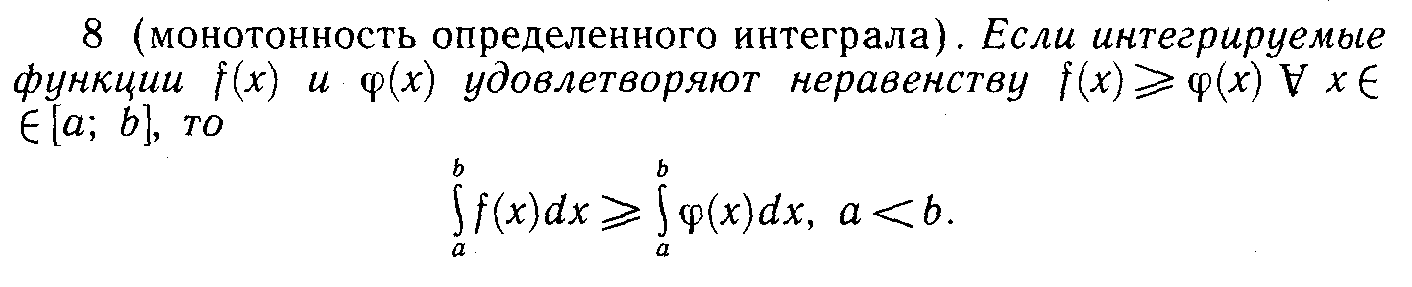
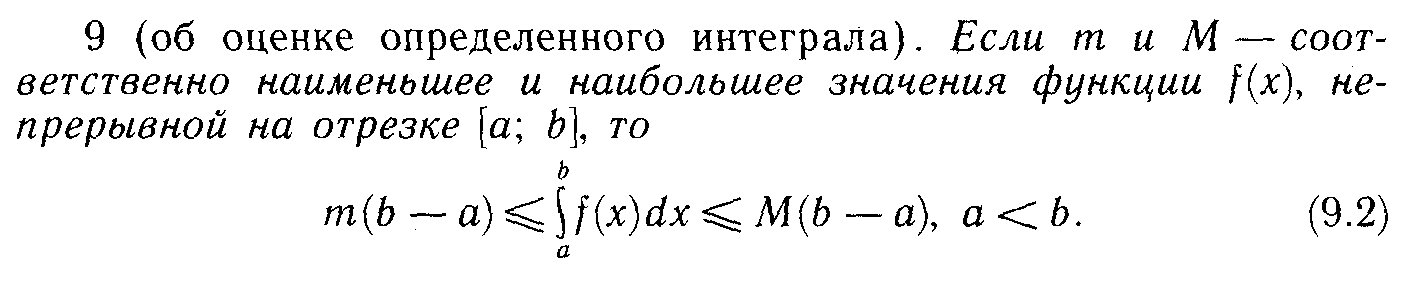
14. Теорема о существовании точных границ у ограниченного мн-ва.

Опр. Мн-во Х, входящее в R называется ограниченым сверху, точно тогда, когда существует b, принадлежащее R, что для любого х из мн-ва Х х<b.

Опр. Мн-во Х, входящее в R называется ограниченым снизу, точно тогда, когда существует а, принадлежащее R, что для любого х из мн-ва Х а<=x.

Опр. Множество, ограниченое сверху и снизу наз. ограниченным.

Опр. Наибольшее среди всех чисел, ограничивающих снизу мн-во Х, входящее в R, называется его нижней гранью - inf {X}.

Опр. Наименьшее среди всех чисел, ограничивающих сверху мн-во Х, входящее в R, называется его верхней гранью - sup {X}.

Т-ма: Всякое ограниченное сверху непустое числовое мн-во имеет верхнюю грань, а всякое ограниченое снизу непустое числовое мн-во имеет нижнюю грань.

Док-во: Пусть Х – ограниченое сверху непустое числовое мн-во из R, а Y – множество всех чисел, ограничивающих сверху данное множество Х. Тогда имеется y из Y, такое, что для любого х из Х, x<=y, где x, y – любые числа из Х и Y. По св-ву непрерывности существеуeт В такое, что для любого х из Х и для любого у из У имеет место x<=В<=y. Т.е. x<=В есть В - ограничивает сверху Х. В<=y есть В - ограничивает снизу У и, следовательно, является наименьшим из всех ограничивающих мн-во Х чисел. Отсюда по опр. Следует, что В = sup {X}. Для мн-ва, ограниченого снизу – док-во аналогично.