Расчет по прочности нормальных сечений.

Предварительно проверяем высоту сечения панели покрытия из условия обеспечения прочности при соблюдении необходимой жесткости по формуле:

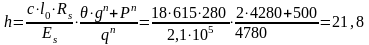22 см

где qⁿ=gⁿ+Рⁿ=4780 Н/м.

Принятая высота сечения h=22 см достаточна. Отношение h_f¹/h=3,8/22=0,1730,1; в расчет вводим всю ширину полки b_f¹=147 cм. Вычисляем по формуле:

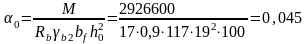
где h₀=h-a=22-3=19 см.

По таблице находим =0,05, =0,975. Высота сжатой зоны x=h₀=0,05*19=0,95h_f¹=3,8 cм – нейтральная ось проходит в пределах сжатой полки.

Площадь сечения продольной арматуры:

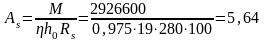см²

Предварительно принимаем 6Ø12 АII, А_s=9,05 см², а также учитываем сетку С-1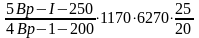 (ГОСТ 8478-81), А_s=6*0,116=0,696 см², ∑А_s=0,696+9,05=9,75 см²; стержни диаметром 12 мм распределяем по два в крайних ребрах и два в двух средних ребрах.

Расчет по прочности наклонных сечений.

Проверяем условие необходимости постановки поперечной арматуры для многопустотных панелей, Q_max=19,04 кН.

Вычисляем проекцию с наклонного сечения по формуле:

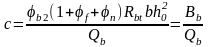
Где _b2=2 – для тяжелого бетона; _f - коэффициент, учитывающий влияние свесов сжатых полок; в многопустотной плите при семи ребрах:

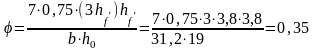0,5;

_n=0, ввиду отсутствия усилий обжатия значение

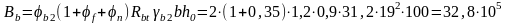
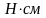
В наклонном расчетном сечении 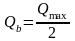, следовательно,

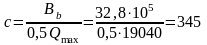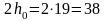см > см.

Принимаем с=38 см, тогда 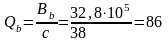кН>Q=19,04 кН. Следовательно, поперечная арматура по расчету не требуется.

Поперечную арматуру предусматриваем из конструктивных условий, располагая ее с шагом:

Sh/2=22/2=11 см, а также S15 см.

Назначаем поперечные стержни диаметром 6 мм класса А-1 через 10 см у опор на участках длиной ¼ пролета. В средней ½ части панели для связи продольных стержней каркаса по конструктивным соображениям ставим поперечные стержни через 0,5 м. Если нижнюю сетку С-1 включить рабочие продольные стержни, то приопорные каркасы можно оборвать в ¼ пролета панели.

Определение прогибов.

Момент в середине пролета от полной нормативной нагрузки Мⁿ=25763 ; от постоянной и длительной нагрузок М_ld=23068 ; от кратковременной нагрузки М_cd=2695 .

Определим прогиб панели приближенным методом, используя значения _lim. Для этого предварительно вычислим:

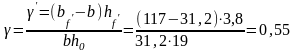
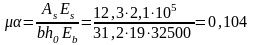
По таблице 2.20 находим _lim=20 при =0,1 и арматуре класса А-II.

Общая оценка деформативности панели по формуле:

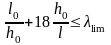
так как 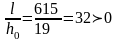, второй член левой части неравенства ввиду малости не учитываем и оцениваем по условию h₀/l≤_lim:

;

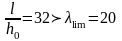условие не удовлетворяется, требуется расчет прогибов.

Прогиб в середине пролета панели от постоянных и длительных нагрузок

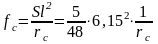
где 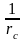- кривизна в середине пролета панели, определяем по формуле:

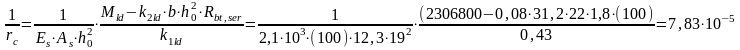см^-1

здесь коэффициенты k_1ld=0,43 и k_2ld=0,08 приняты по таблице 2.19 в зависимости от =0,1 и =¹0,55 для двутавровых сечений.

Вычисляем прогиб f следующим образом

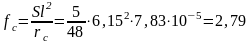
f_max=Sl²/r_c=5/48*5,85²*7,83*10^-5=2,79 с,. что меньше f_lim=3 см для элементов покрытий с плоским потолком при l<6 м.

Расчет панели по раскрытию трещин.

Панель покрытия, согласно СНиП, относится к третьей категории трещиностойкости как элемент, эксплуатируемый в закрытом помещении и армированный стержнями, из стали класса А-II. Предельно допустимая ширина раскрытия трещин а_crc1=0,4 мм и а_crc2=0,3 мм.

Для элементов третьей категории трещиностойкости, рассчитываемых по раскрытию трещин, нормальных к продольной оси, при действии кратковременных и длительных нагрузок должно соблюдаться условие

а_crc= а_crc1- а_crc2+ а_crc3< а_crc,max,

где а_crc1- а_crc2 – приращение ширины раскрытия трещин в результате кратковременного увеличения от постоянной и длительной до полной;

а_crc3- ширина раскрытия трещин от длительного действия постоянных и длительных нагрузок.

Ширину раскрытия трещин определяем по формуле:

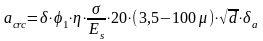
для ; вычисления а_crc используем данные норм и величины, полученные при определении прогибов:

=1- как для изгибаемых элементов;

=1- для стержневой арматуры периодического профиля;

d=1,2 см- по расчету;

E_s=2,1*10⁵ МПа – для стали класса А-11;

_a=1, так как а₂=3 см < 0,2/h = 0,2/22=4,4 см.

_l=1 - при кратковременных нагрузках и _l=1,6-15- при постоянных и длительных нагрузках;

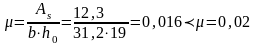
принимаем =0,016, тогда _l=1,6-15=1,6-15*0,016=1,36;

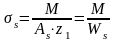
Определяем z_1:

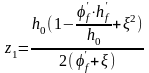
здесь _f=0,55; h_f¹ /h₀=3,8/22=0,173; h₀=19 см; по формуле находим :

=1/(1,8+(1+5(+)/10)

=_f¹(1-h_f¹/(2h₀))=0,55(1-3,8/(2*19))=0,495

Значение  от действия всей нормативной нагрузки:

=Mⁿ/R_b,ser b h₀²=2311600/22*(100)*117*19²=0,027;

=A_s E_s/bh₀ E_b=9,978*2,1*10⁵/32,6*19*32500=0,104.

Вычисляем  при кратковременном действии всей нагрузки:

=1/(1,8+(1+5(0,027+0,495)/10*0,104)=0,189> h_f¹ /h₀=0,173;

продолжаем расчет как тавровых сечений.

Значение z₁ по формуле:

z₁=19(1-(0,55* 0,173+0,189²)/2(0,55+0,189))=17,3 см.

Упругопластический момент сопротивления железобетонного таврового сечения после образования трещин:

W_s=A_s z₁=12,3*17,3=213 см³.