4.4. Дифференцирование тригонометрических функций

Пусть сначала f(x)=sinx. Рассмотрим приращение этой функции в точке х₀: f = sin(x₀+x)–sinx₀. Применим формулу разности синусов: sin–sin=2sin cos . Тогда f=2sin cos , = 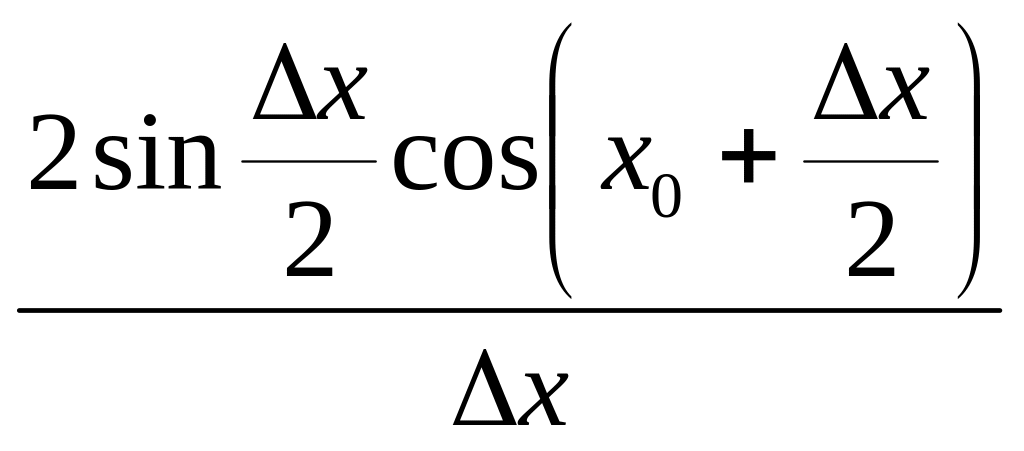. Воспользуемся эквивалентностью: если у=у(х)0 при х0, то бесконечно малые siny и у эквивалентны. В данном случае у = 0 при х0, поэтому sin  . Значит, =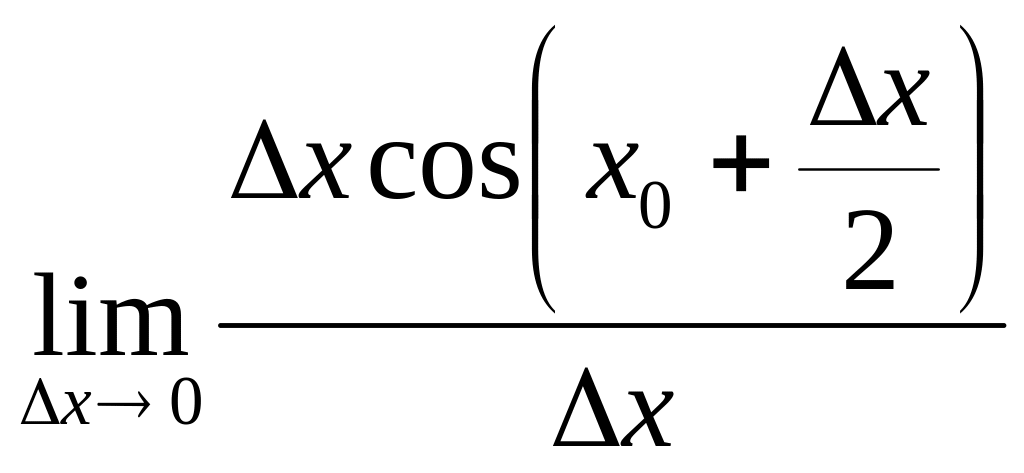 = . А этот предел равен cosx₀, так как cosx – непрерывная функция. Итак,

=cosx.

Пусть теперь f(x)=cosx. По формуле приведения получаем f(x)=sin . Используем правило дифференцирования сложной функции: = cos (–1) = –sinx. Итак,

= –sinx.

Пример. Найдем производную функции f(х)= . Здесь f(х)=w(v(u(х))), u(х)=lnx, = , v(z)=sinz, =cosz, w(t)= , = . По правилу дифференцирования сложной функции = . Подставляя t=sinz, z= lnx, получаем: = 

Формулы производных тангенса и котангенса получаем, используя правило дифференцирования частного:

= , = – .

4.5. Дифференцирование обратных тригонометрических функций

Для того чтобы получить формулы производных для обратных тригонометрических функций, нам понадобится следующее утверждение.

Теорема. Пусть функция g(y) непрерывна и монотонна на отрезке [a;b] и дифференцируема в точке у₀(a;b), причем 0. Пусть g(y₀)=х₀. Тогда обратная функция f(x) дифференцируема в точке х₀ и = .

Доказательство. Так как функции f(x) и g(y) – взаимно обратные, то g(f(x))=х. Тогда по правилу дифференцирования сложной функции =1, где 0, откуда и следует равенство = , что и требовалось доказать.

Пример. Пусть f(x)= , тогда обратная функция g(y)=a^y и = a^ylna. По только что доказанной теореме = = = – уже известная нам формула производной логарифмической функции.

Найдем производную функции f(x)=arcsinx. Обратная функция g(y) = siny, = cosy. Значит, = =

= = . Пусть arcsinx=. Тогда sin=x,

–  . Поэтому cos²=1–x², cos0, а значит, cos= , то есть cos(arcsinx) = . Итак,

= .

Чтобы найти производную арккосинуса, достаточно использовать равенство arcsinx+arccosx = ; arccosx = – arcsinx, поэтому

= – .

Пусть теперь f(x)=arctgx. Обратная функция g(y) = tgy, = . Значит, = = cos²y = cos²(arctgx). Пусть arctgx=. Тогда tg=x, tg²+1=1+x², cos²= , то есть cos²(arctgx) = . Итак,

= .

Чтобы найти производную арккотангенса, достаточно использовать равенство arctgx+arcctgx = ; arcctgx = – arctgx, поэтому

= – .

Примеры. 1)Найдем дифференциал функции f(x)=(arctg )³ в точке х₀=1, если dx=0,08. f(x)=w(v(u(x))), где u(x) = , v(z) = arctg z, w(t) = t³. Поэтому = =3(arctg )^{2 . ,} = .

Значит, df = ^.0,08 = .

2)Найдем производную функции f(x)=arcsin(sinx). f(x)= v(u(x)), где u(x)=sinx, v(z) = arcsin z. Поэтому = = = . Таким образом, не существует, если cosx=0; = –1, если cosx<0; = 1, если cosx>0. Вот как выглядит график этой функции.



4.6. Дифференцирование гиперболических функций

Гиперболическими функциями называются следующие четыре функции:

shx= – синус гиперболический;

chx= – косинус гиперболический;

thx= – тангенс гиперболический;

cthx= – котангенс гиперболический.

Свойства этих функций во многом совпадают со свойствами обычных тригонометрических функций: например, гиперболические тангенс и котангенс равны, соответственно, отношению синуса к косинусу и косинуса к синусу. Формула двойного аргумента: sh2x=2shxchx – такая же, как для синуса двойного угла. Но, в отличие от «тригонометрической единицы», сумма квадратов гиперболических синуса и косинуса равна не единице, а ch2x. А «гиперболическая единица» равна не сумме, а разности этих квадратов:

ch²x– sh²x=1.

Поэтому система задает на плоскости гиперболу, так же как система задает окружность. Отсюда и название гиперболических функций. Их свойства видны из следующих графиков.

Синус гиперболический:

Косинус гиперболический:

Тангенс гиперболический

Котангенс гиперболический:

Формулы производных гиперболических функций получаются из производных показательной функции с помощью правил дифференцирования суммы, частного и сложной функции:

; ; ; .