4.3.Собственные векторы линейного отображения

Пусть f : Rⁿ®Rⁿ – линейное отображение с матрицей А. Ненулевой вектор ÎRⁿ называется собственным вектором отображения f (или матрицы А), если существует такое число λ, что f( )=λ . Число λ при этом называется собственным значением (или собственным числом).

Пусть существует вектор ¹ такой, что f( )=λ , то есть А =λ , ¹ . Тогда А =λЕ , А –λЕ = . Это значит, что однородная система (А–λЕ) = имеет ненулевое решение; поэтому определитель матрицы системы равен нулю. Таким образом, число λ является собственным значением матрицы А тогда и только тогда, когдаúА–λЕê=0. Полученное уравнение относительно λ называется характеристическим уравнением матрицы А. Чтобы найти собственные значения и собственные векторы матрицы А, надо составить и решить характеристическое уравнение; а затем для каждого из полученных собственных значений найти ненулевые решения системы (А–λЕ) = , то есть собственные векторы.

Примеры. Найдем собственные значения и собственные векторы следующих матриц.

1). А= . Тогда úА–λЕê= =

=(7–λ)(–2–λ)+8=λ²–5λ–6. Получаем характеристическое уравнение: λ²–5λ–6=0. Его корни λ₁= –1 и λ₂=6 являются собственными значениями матрицы. Найдем для каждого из них собственные векторы.

Пусть λ= –1, А–λЕ= , и система (А–λЕ) = равносильна уравнению –х₁–х₂=0. Общее решение системы: =(a,–a). Значит, собственные векторы, соответствующие собственному значению –1, имеют вид: =(a,–a), где a¹0. Иначе можно записать так: =a (1,–1), где a¹0.

Пусть λ=6, А–λЕ= , и система (А–λЕ) = равносильна уравнению х₁+8х₂=0. Общее решение системы: =(–8a,a). Значит, собственные векторы, соответствующие собственному значению 6, имеют вид: =(–8a,a), где a¹0. Иначе можно записать так: =a (–8,1), где a¹0.

2). А=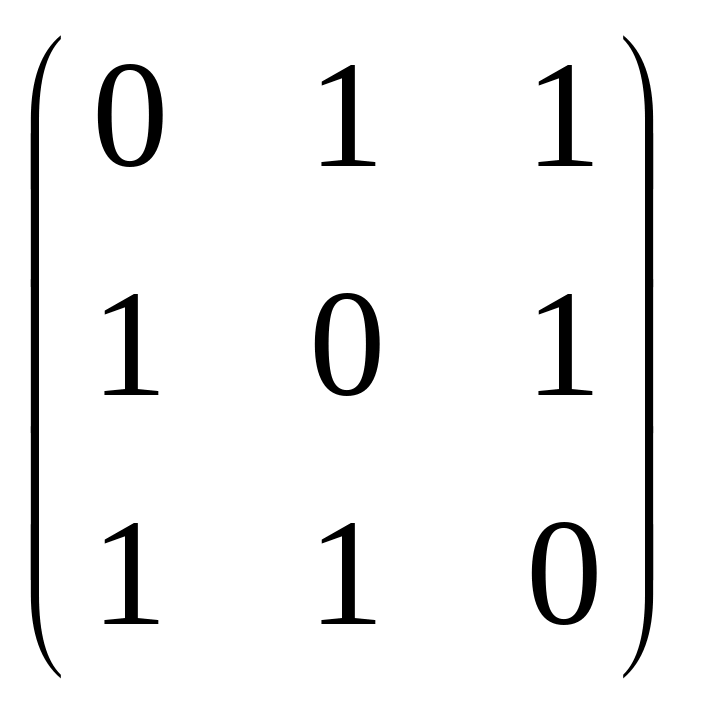 . Тогда úА–λЕê= =

=–λ(λ²–1)–1(–λ–1)+1(1+λ)=(λ+1)(–λ²+λ+2). Получаем характеристическое уравнение: (λ+1)(–λ²+λ+2)=0. Его корни λ₁= –1 и λ₂=2 являются собственными значениями матрицы. Найдем для каждого из них собственные векторы.

Пусть λ= –1, А–λЕ= , и система (А–λЕ) = равносильна уравнению х₁+х₂+х₃=0. Общее решение системы: =(a,β,–a–β). Значит, собственные векторы, соответствующие собственному значению –1, имеют вид: =(a,β,–a–β), где a²+β²¹0. Иначе можно записать так: =a(1,0,–1)+ β(0,1,–1), где a²+β²¹0.

Пусть λ=2, А–λЕ=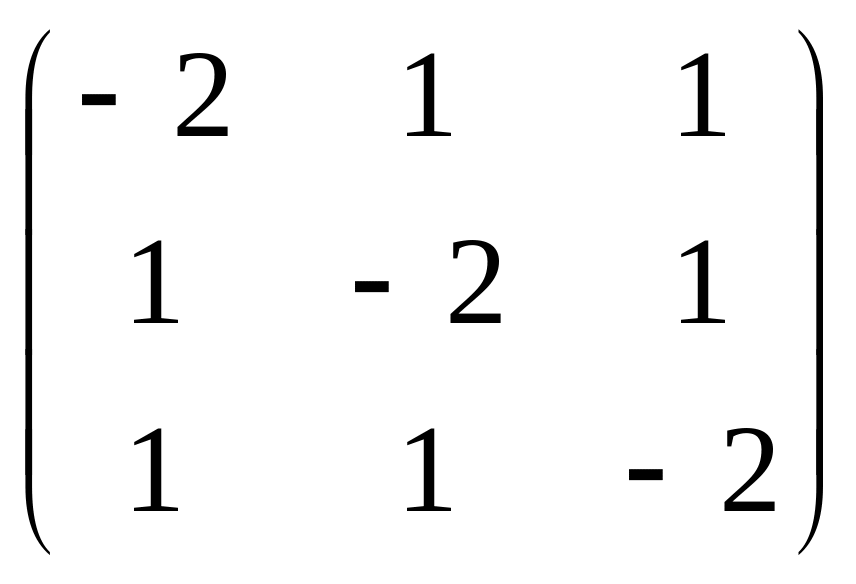 ; система

(А–λЕ) = равносильна системе . Общее решение системы: =(a,a,a). Значит, собственные векторы, соответствующие собственному значению 2, имеют вид: =(a,a,a), где a¹0. Иначе можно записать так: =a(1,1,1), где a ¹0. ·

СПИСОК ЛИТЕРАТУРЫ

1. Арутюнян Е.Б., Родина Е.В. Аналитическая геометрия и линейная алгебра – М: МИИТ, 2003.

2. Берман Г.Н. Сборник задач по курсу математического анализа. М. Наука. 1969 г.

3. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. М. Наука. 1973 г.

4. Кудрявцев Л.Д. Курс математического анализа. Части 1, 2. М. Высшая школа. 1981 г.

5. Кузнецов Л.А. Сборник заданий по высшей математике. М. Высшая школа. 1983 г.

Св. план 2009 г., поз.90

Арутюнян Елена Бабкеновна

Математика