4. Линейные пространства и линейные отображения

4.1.Линейные отображения Rn

Соответствие = f( ) между векторами пространства Rⁿ называется линейным отображением, если для любых векторов , и любых чисел a, β справедливо равенство: f(a +β )=af( )+βf( ). Соответствие = f( ) обозначается f : Rⁿ®Rⁿ.

Примеры. 1) Пусть f : R²®R², где f( )=( х₁– х₂; х₁+ х₂); при этом отображении вектор = f( ) получается из вектора поворотом на 60^о. Проверим, является ли это отображение линейным. Пусть =(а₁;а₂), =(b₁;b₂), a, βÎR. Тогда:

f( ) = ( а₁– а₂; а₁+ а₂); f( ) = ( b₁– b₂; b₁+ b₂); af( )+βf( ) = a( а₁– а₂; а₁+ а₂)+ +β( b₁– b₂; b₁+ b₂). С другой стороны, f(a +β )=( (aа₁+βb₁)– (aа₂+βb₂); (aа₁+βb₁)+ + (aа₂+βb₂)). Как видно, f(a +β )=af( )+βf( ), то есть данное отображение – линейное.

2) Пусть f : R³®R³, где f( )=(х₁;0;0); при этом отображении вектор = f( ) получается из вектора проектированием на ось Ох. Проверим, является ли это отображение линейным. Пусть =(а₁;а₂;а₃), =(b₁;b₂;b₃), a, βÎR. Тогда: f( )=(а₁;0;0); f( )=(b₁;0;0); af( )+βf( )=a(а₁;0;0)+

+β(b₁;0;0). С другой стороны, f(a +β )=(aа₁+βb₁;0;0). Как видно, f(a +β )=af( )+βf( ), то есть данное отображение – линейное.

3) Пусть f : R³®R³, где f( )=(0;х₂;х₃); при этом отображении вектор = f( ) получается из вектора проектированием на плоскость yОz. Проверим, является ли это отображение линейным. Пусть =(а₁;а₂;а₃), =(b₁;b₂;b₃), a, βÎR. Тогда: f( )=(0;а₂;а₃); f( )=(0;b₂;b₃); af( )+βf( )= a(0;а₂;а₃)+β(0;b₂;b₃). С другой стороны, f(a +β )=(0;aа₂+

+βb₂;aа₃+βb₃). Как видно, f(a +β )=af( )+βf( ), то есть данное отображение – линейное.

4) Пусть f : R²®R², где f( )=(х₁+1;х₂–2). При этом отображении вектор = f( ) получается из вектора сдвигом на вектор с координатами (1;–2). Проверим, является ли это отображение линейным. Пусть =(а₁;а₂), =(b₁;b₂), a, βÎR. Тогда: f( )=(а₁+1;а₂–2); f( )=(b₁+1;b₂–2); af( )+βf( ) = a(а₁+1;а₂–2)+β(b₁+1;b₂–2) =(aа₁+a+βb₁+ +β; aа₂–2a+βb₂–2β). С другой стороны, f(a +β )=(aа₁+

+b₁+1; aа₂+βb₂–2). Как видно, f(a +β )¹af( )+βf( ), то есть данное отображение – не линейное.·

Пусть f : RⁿRⁿ – линейное отображение, , ..., – базис Rⁿ. Запишем разложения векторов f( ), ..., f( ) по этому базису: f( )=а₁₁ +...+а_n1 , …, f( )=а_1n +...+а_nn . Тогда, если =х₁ +...+х_n , то, в силу линейности отображения, f( )=х₁(а₁₁ +...+а_n1 )+...+х_n(а_1n +...+а_nn )=

=(х₁а₁₁+... х_nа_1n) +...+(х₁а_n1+...+х_nа_nn) . Пусть А=(а_ij). Тогда для любого  Rⁿ будет f( )=А . Матрица А называется матрицей линейного отображения f в данном базисе.

Примеры. Рассмотрим линейные отображения из предыдущего примера и составим их матрицы в стандартных базисах. 1) f : R²R², f( )=( х₁– х₂; х₁+ х₂). f( )=( ; ), f( )=(– ; ). Значит, А= .

2) f : R³R³, f( )=(х₁;0;0). f( )=(1;0;0), f( )=(0;0;0), f( )=(0;0;0). Значит, А= .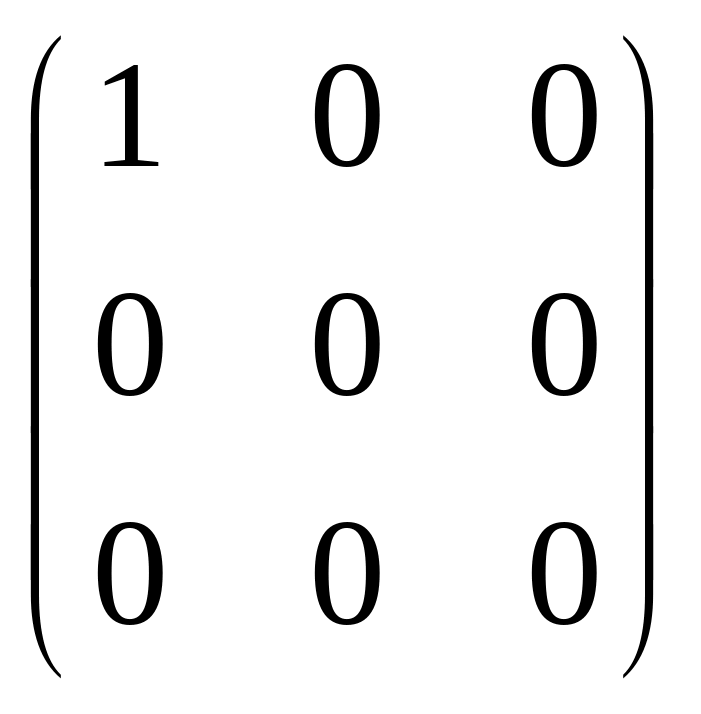

3) f : R³R³, f( )=(0;х₂;х₃). f( )=(0;0;0), f( )=(0;1;0), f( )=(0;0;1).

Значит, А= .

4.2.Линейные подпространства Rn

Подмножество LRⁿ называется линейным подпространством, если для любых векторов , L и любых чисел , β вектор  +β принадлежит L.

Примеры. 1) Подмножество L пространства R², состоящее из векторов вида =(х₁;2х₁), является линейным подпространством: если =(а₁;2а₁) и =(b₁;2b₁), то для любых , β получаем  +β = (а₁+βb₁; 2(а₁+βb₁)), то есть  +β L.

2) Подмножество L пространства R², состоящее из векторов вида =(х₁;2х₁–1), не является линейным подпространством: если =(а₁;2а₁–1) и =(b₁;2b₁–1), то, например, для =1, β=1 получаем  +β = (а₁+b₁; 2(а₁+b₁)–2), то есть  +β L.

3) Пусть Rⁿ – произвольные векторы. Тогда множество L( ), состоящее из всевозможных линейных комбинаций данных векторов, является линейным подпространством. Его называют линейной оболочкой векторов .

4) Пусть f : RⁿRⁿ – линейное отображение. Подмножество Kerf, состоящее из всех векторов , для которых f( )= , называется ядром отображения f. Подмножество Imf, состоящее из всех векторов , для которых существует такой вектор , что f( )= , называется образом отображения f. Можно доказать, что Kerf и Imf являются линейными подпространствами. Размерность ядра называется дефектом отображения f, размерность образа – рангом отображения f. Рассмотрим линейные отображения из предыдущего пункта, найдем для каждого ядро и образ, определим ранг и дефект.

1. f : R²R², f( )=( х₁– х₂; х₁+ х₂). Kerf={ R²: f( )= }. Определитель системы 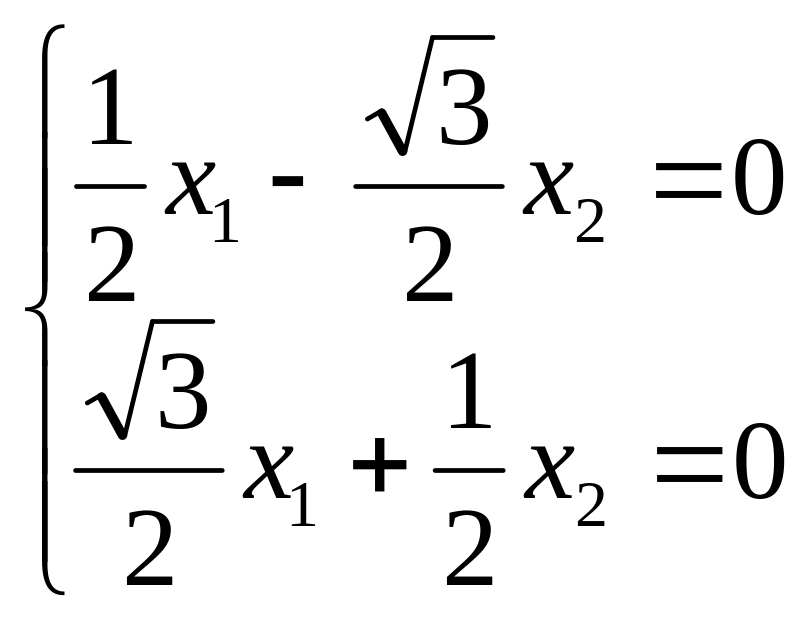не равен нулю, поэтому получаем единственное решение: = . Итак, Kerf={ }. Значит, дефект отображения равен 0. Чтобы найти Imf, надо определить, при каких у₁ и у₂ имеет решение система . Поскольку ее определитель не равен нулю, то она имеет решение при любых у₁ и у₂. Значит , Imf = R², и ранг отображения равен 2.

2. f : R³R³, f( )=(х₁;0;0). Kerf тогда и только тогда, когда х₁=0. Значит, Kerf ={(0;x₂;x₃)}={x₂ +x₃ }, и дефект отображения равен 2. Imf состоит из таких векторов , что у₂=у₃=0, то есть Imf ={у₁ }, и ранг отображения равен 1.

3. f : R³R³, f( )=(0;х₂;х₃). Kerf тогда и только тогда, когда х₂=х₃=0. Значит, Kerf ={(x₁;0;0)}={x₁ }; дефект отображения равен 1. Imf состоит из таких векторов , что у₁=0, то есть Imf ={у₂ +у₃ }; ранг отображения равен 2.