1.2. Линейная зависимость векторов

Пусть , , ..., Rⁿ, ₁, ₂, ..., _kR. Выражение ₁ +₂ +...+_k называется линейной комбинацией векторов , , ..., с коэффициентами ₁, ₂, ..., _k. Линейная комбинация называется тривиальной, если все коэффициенты равны нулю. Векторы , , ..., называются линейно зависимыми, если существует их нетривиальная линейная комбинация, равная . В противном случае векторы называются линейно независимыми.

Замечание. Если k=1 и система векторов линейно зависима, то существует ₁0 такое, что ₁ = . Значит, = . Итак, система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор – нулевой. Если k2 и система векторов линейно зависима, то существуют ₁, ₂, ..., _k, не все равные нулю, такие, что ₁ +₂ +...+_k = . Будем считать, что ₁0 (иначе векторы можно просто перенумеровать). Тогда получим: = – –...– . Итак, система, состоящая более чем из одного вектора, линейно зависима тогда и только тогда, когда хотя бы один вектор системы является линейной комбинацией остальных.

Перечислим без доказательства свойства линейно зависимых и линейно независимых систем векторов.

1. Система, содержащая нулевой вектор, линейно зависима.

2. Подсистема линейно независимой системы линейно независима.

3. Система, содержащая линейно зависимую подсистему, линейно зависима.

4. Если система линейно независима, а добавление одного вектора делает ее зависимой, то этот вектор является линейной комбинацией векторов системы.

5. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

6. Назовем систему векторов лестничной, если векторы можно занумеровать так, что у вектора с номером m все компоненты от первой до (m–1)-ой равны нулю, а m-ая компонента отлична от нуля. Лестничная система линейно независима.

7. Ортогональная система линейно независима.

Пример. Проверим, являются ли линейно зависимыми векторы =(1;2;–3;3;1), =(2;–1;1;1;1), =(–3;4;–5;1;–1), = (5;0;–1;5;3). Пусть ₁ +₂ +₃ +₄ = . Тогда все координаты пятимерного вектора в левой части этого равенства равны нулю. Выписав эти координаты, получим систему уравнений:

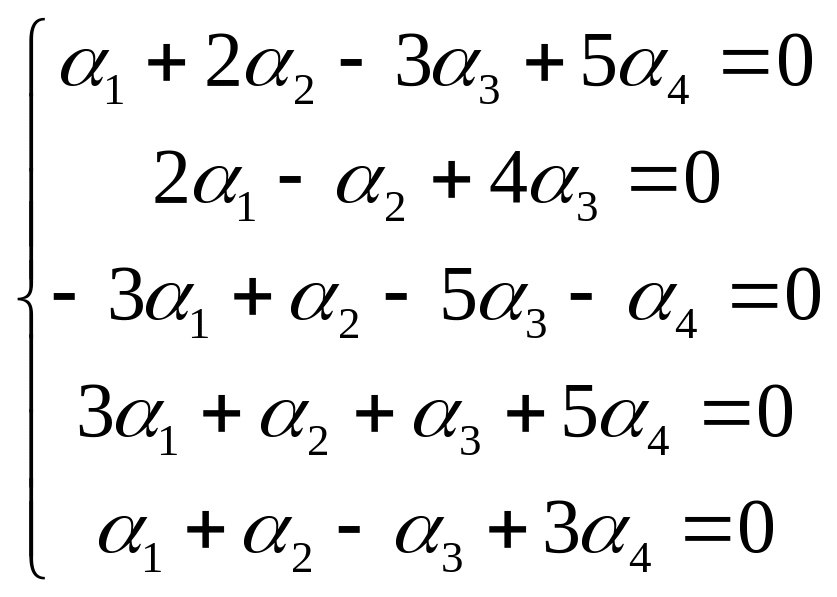. Выразим из второго уравнения ₂ и подставим в остальные уравнения:

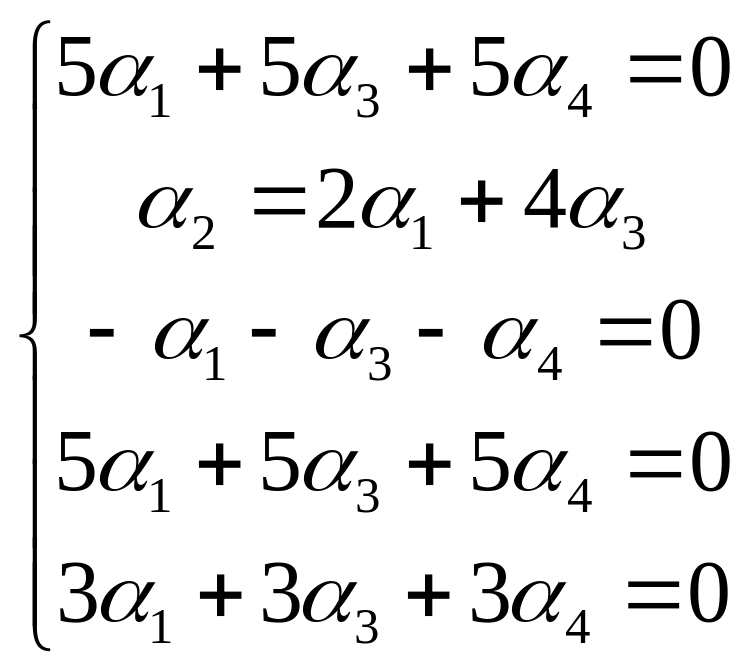. Здесь первое, третье, четвертое и пятое уравнения равносильны. Остается система: . Отсюда получаем, что , где ₁ и ₃ – любые числа. Нетривиальная линейная комбинация получится, если хотя бы одно из них не равно нулю. Пусть, например, ₁=0, ₃ = –1. Тогда ₂= –4, ₄ = 1. Получаем нетривиальную линейную комбинацию, равную : –4 – + = . Значит, векторы линейно зависимы.

1.3. Базис и ранг системы векторов

Базисом системы векторов называется такая ее линейно независимая подсистема, что любой вектор системы является линейной комбинацией векторов этой подсистемы. Можно доказать, что любые два базиса одной и той же системы содержат одинаковое число векторов. Это число называется рангом системы векторов. Ранг системы равен числу векторов в системе тогда и только тогда, когда система линейно независима.

Пример. В предыдущем пункте мы показали, что система векторов =(1;2;–3;3;1), =(2;–1;1;1;1),

=(–3;4;–5;1;–1), =(5;0;–1;5;3) является линейно зависимой: ₁ +(2₁+4₃) +₃ +(–₁–₃) = при любых ₁ и ₃. Пусть, например, ₁=1, ₃=0. Тогда получаем равенство: +2 – = , – откуда = –2 + . Пусть теперь ₁=0, ₃=1. Тогда получаем: 4 + – = , – откуда = –4 + . Таким образом, векторы и являются линейными комбинациями векторов и . Так как и не коллинеарны, а значит, линейно независимы, то они образуют базис данной системы. Поэтому ранг этой системы равен 2. Можно показать, что в данном случае любые два вектора системы образуют ее базис.

В случае, когда рассматриваемая система векторов совпадает со всем пространством, вместо слова «ранг» используют слово «размерность»; размерность обозначается знаком dim. Покажем, что dimRⁿ=n. Рассмотрим набор векторов: =(1;0;...;0), =(0;1;0;...;0), =(0;0;1;0;...;0), ..., =(0;...;0;1). Тогда любой вектор = (а₁, а₂, ..., а_n) можно представить в виде а₁ +а₂ +...+а_n . С другой стороны, векторы , ,..., образуют лестничную систему и, следовательно, являются линейно независимыми. Значит, эти векторы образуют базис пространства Rⁿ. Этот базис обычно называют стандартным. Можно показать, что любые n линейно независимых векторов пространства Rⁿ образуют базис.