7.8. Кривизна плоской кривой
Рассмотрим две точки
А и В гладкой плоской кривой. Пусть
– угол между касательными к этой кривой
в точках А и В (напомним, что угол между
прямыми – острый или прямой). Отношение
,
где s – длина дуги АВ,
назовем средней кривизной этой
дуги. Средняя кривизна, таким образом,
– функция длины дуги. Пусть точка А
фиксирована, а точка В – переменная.
Тогда предел k средней
кривизны дуги АВ при приближении точки
В к точке А называется кривизной данной
кривой в точке А. Другими словами,
k =
(если эта производная положительна). В
общем же случае k
=
.
Примеры. 1)
Рассмотрим окружность радиуса R.
Тогда длина s дуги АВ
равна R,
где – угол между
касательными к окружности в точках А и
В. Значит, =
,
то есть k =
=
.
Итак, окружность – это кривая постоянной
кривизны.
2) Рассмотрим прямую. Тогда угол между любыми двумя касательными равен 0. Поэтому k = = 0. Итак, кривизна прямой в любой точке равна нулю.
Пусть данная кривая
задана параметрически:
,
– где
и
непрерывны. Тогда
=
(по формуле дифференцирования функции,
заданной параметрически). Примем без
доказательства, что
=
.
С другой стороны,
= arctg
=
arctg
;
значит,
=
=
.
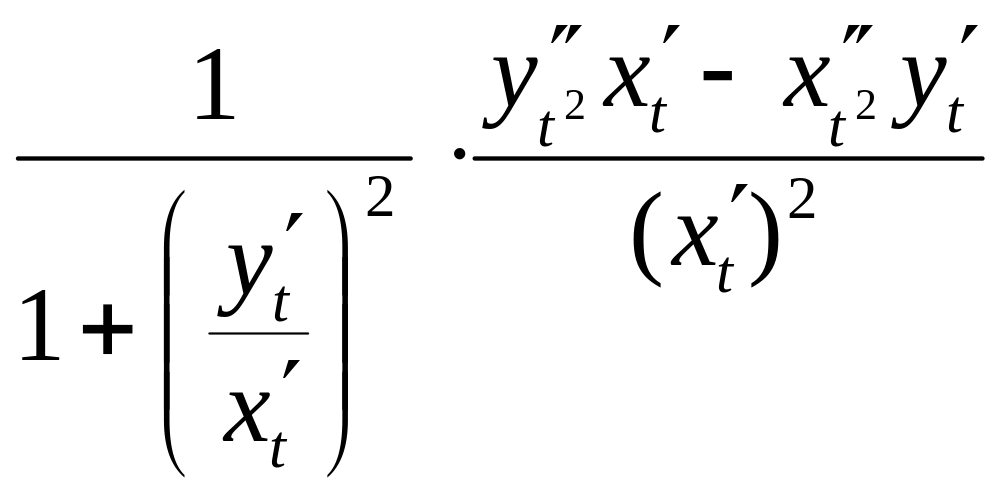Отсюда k =
.
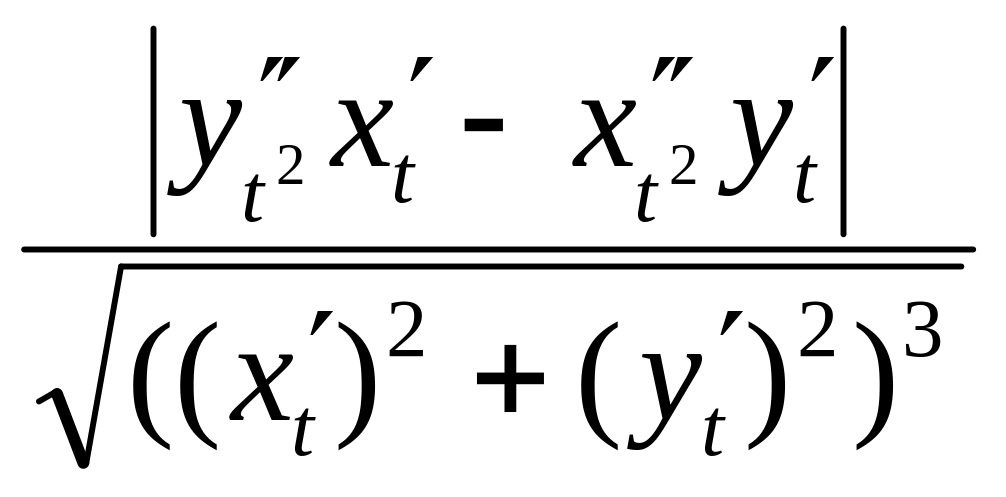Это общая формула кривизны плоской
кривой.
Пример. Найдем
кривизну циклоиды:
.
Имеем:
=a(1–cost),
=
asint,
=
asint,
=
acost.
Отсюда k =
=
=
=
=
.
Пусть, в частности,
кривая задана уравнением y=f(x),
где
непрерывна. Тогда можно считать, что
x=t,
y=f(t).
Имеем:
=1,
=
0,
=
,
=
.
Значит, в этом случае k
=
.
Пример. Найдем кривизну линии y = –x3:
– в
точке с абсциссой
.
Имеем: f(x)=
–x3 ,
=
–3х2,
=
–6х. Отсюда k
=
=
=
=
=
=
=
.
Пусть, наконец,
кривая задана в полярных координатах:
=(),
где
непрерывна. Тогда x
= ()сos,
y=()sin.
Имеем:
=
,
=
,
=
,
=
.
Значит, в этом случае
k =
.
Пример. Найдем кривизну кардиоиды = a(1+cos):
– в
точке с полярным углом
.
Имеем:
=
–asin,
=
–acos.
Отсюда
k=
=
=
=
=
=
.
7.9. Вектор-функция скалярного аргумента
Рассмотрим
пространственную кривую, заданную
параметрически:
.
Эту кривую можно рассматривать как
множество концов вектора {x(t),
y(t),
z(t)}
с началом в начале координат. Этот вектор
будем обозначать
и называть вектор-функцией скалярного
аргумента t. Сама
исходная кривая при этом называется
годографом переменного вектора
.
Примеры.
1)Годографом вектор-функции
={t,t,t}
является прямая
.
2)Годографом вектор-функции
={1,1,t}
является прямая
.
3)Годографом вектор-функции
={сht,1,sht}
является сечение гиперболического
цилиндра x2–z2=1
плоскостью у=1.
Если
при некотором значении t0
существует
,
то он называется производной
вектор-функции в точке t0
и обозначается
.
Вектор
имеет координаты {
,
,
}.
Он направлен по касательной к годографу
в направлении возрастания параметра
t.
Пример.
Годографом вектор-функции
={сost,2,sint}
является сечение кругового цилиндра
x2+z2=1
плоскостью у=2, то есть окружность
радиуса 1. Докажем, что векторы
и
перпендикулярны при любом значении t:
=
{–sint,0,сost}.
Значит,
.
=
–sintсost+sintсost
= 0, то есть
,
что и требовалось доказать. Заметим,
что геометрически это равносильно
хорошо известному факту: касательная
к окружности перпендикулярна радиусу,
проведенному в точку касания.
Свойства производной вектор-функции аналогичны свойствам обычной производной:
1.
.
2.
.
3.
=
.
4.
.
5.
.
Поскольку вектор является направляющим вектором касательной, проведенной к годографу вектор-функции в точке (x(t0),y(t0),z(t0)), то уравнение касательной к пространственной кривой в точке (x(t0),y(t0),z(t0)) имеет вид:
=
=
.
Плоскость,
проходящая через точку (x(t0),y(t0),z(t0))
перпендикулярно касательной, называется
нормальной плоскостью пространственной
кривой. Ее уравнение имеет вид:
(
)+
(
)+
(
)=0.
Пример.
Составим уравнения касательной и
нормальной плоскости к винтовой линии
при t0=
.
Уравнение
касательной:
.
Уравнение нормальной плоскости: –1(x)+0(y–1)+1(z– )=0, или x–z+ =0.