7.4. Отыскание наибольшего и наименьшего значений функции, непрерывной на отрезке

Пусть функция f(x) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Как известно, в этом случае она достигает на отрезке своего наибольшего значения и своего наименьшего значения. Для нахождения этих значений поступают так: определяют точки интервала (a;b), в которых производная равна нулю или не существует, а затем сравнивают значения функции в этих точках и на концах отрезка.

Пример. Найдем наибольшее и наименьшее значения функции f(x)=х³–3х²–45х+225 на отрезке [0;6].

1) =3x²–6х–45. Точек, в которых не существует, нет. Найдем точки, в которых =0: 3x²–6х–45=0,

x²–2х–15=0, х= –3 или х=5. Из этих точек интервалу (0;6) принадлежит только точка х=5.

2) Сравним значения функции в точках х=0, х=5, х=6. f(0)=225, f(5)=50, f(6)=63. Значит, наибольшее значение функции на данном отрезке равно 225 и достигается при х=0; наименьшее значение функции на данном отрезке равно 50 и достигается при х=5.

7.5. Исследование функции на выпуклость

Определение 1. Пусть функция f(x) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Функция называется выпуклой вверх (соответственно выпуклой вниз) на отрезке [a;b], если при всех х₁, х₂[a;b] выполняется неравенство: > (соответственно выполняется неравенство: < ).

На рисунке дан график функции, которая выпукла вверх на отрезке [1;4] и выпукла вниз на отрезке [–2;1].

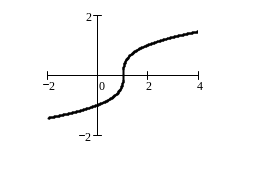
Теорема 7. Пусть функция f(x) непрерывна на отрезке [a;b] и имеет на интервале (a;b) вторую производную. Тогда, если >0 на интервале (a;b), то функция f(x) выпукла вниз на отрезке [a;b]; а если <0 на интервале (a;b), то функция f(x) выпукла вверх на отрезке [a;b].

Доказательство. Возьмем х₁, х₂[a;b]. Пусть, для определенности, х₁<х₂. Имеем: 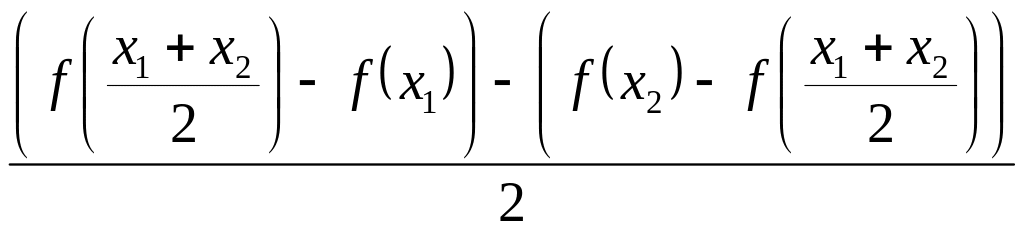= – = . По теореме Лагранжа существуют такие c(х₁; ) и d( ;x₂), что = =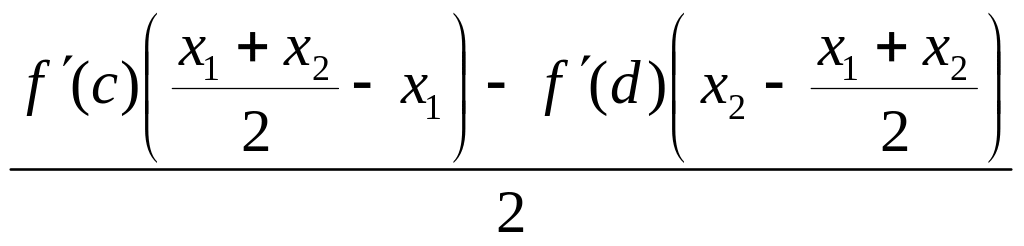

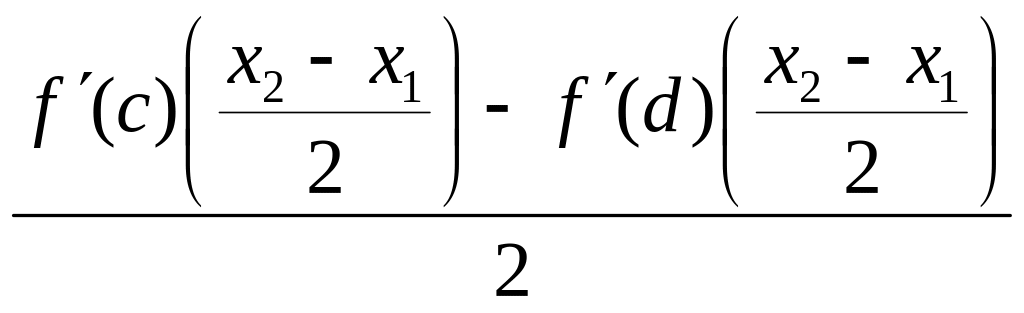= = . Еще раз применим теорему Лагранжа – теперь к функции : существует такое t(c;d), что = (c–d). Итак, = (c–d) . Так как c–d<0, а х₂–х₁>0, то разность  и имеют разные знаки. Значит, если >0 на интервале (a;b), то <0, а если <0 на интервале (a;b), то >0. Поэтому в первом случае функция f(x) выпукла вниз на отрезке [a;b], а во втором случае функция f(x) выпукла вверх на отрезке [a;b], ч.т.д.

Пример. Пусть f(x) = x^, x>0, 0, 1. Тогда = x^(–1), =(–1)x^{(–1)(–2)}. Значит, >0 при x>0, если <0 или >1; <0 при x>0, если 0<<1. Поэтому степенная функция f(x) = x^ на всей области определения выпукла вверх, если 0<<1, и выпукла вниз, если <0 или >1.

Определение 2. Пусть х₀D(f) и существуют отрезки [х₀–; х₀] и [х₀; х₀+] такие, что на одном из них функция f(x) выпукла вверх, а на другом – вниз. Тогда точка х₀ называется точкой перегиба функции f(x).

Теорема 8 (необходимое условие точки перегиба). Пусть функция f(x) непрерывна на отрезке [х₀–;х₀+] и дифференцируема на интервале (х₀–;х₀+), непрерывна в точке х₀. Тогда, если х₀ – точка перегиба, то =0.

Доказательство. Если 0, то, поскольку непрерывна в точке х₀, в некоторой окрестности этой точки сохраняет знак. По теореме 7 это означает, что в некоторой окрестности точки х₀ функция f(x) выпукла вверх или выпукла вниз. А тогда точка х₀ не является точкой перегиба, ч.т.д.

Пример. Заметим, что условие =0 является именно необходимым, но не достаточным условием точки перегиба. Пусть, например, f(x)=х³. Тогда =6х, =0 при х=0. Если х<0, то <0, то есть функция f(x) выпукла вверх; если х>0, то >0, то есть функция f(x) выпукла вниз; значит, х=0 – точка перегиба. Пусть теперь f(x)=х⁴. Тогда =12х², =0 при х=0. Если х<0, то >0, то есть функция f(x) выпукла вверх; если х>0, то >0, то есть функция f(x) выпукла вверх; значит, х=0 не является точкой перегиба. Таким образом, в обоих случаях для точки х=0 выполняется необходимое условие точки перегиба, но во втором случае эта точка не является точкой перегиба.

Теорема 9 (достаточное условие точки перегиба). Пусть функция f(x) непрерывна на отрезке [х₀–;х₀+], дифференцируема на интервале (х₀–;х₀+) и имеет вторую производную на интервалах (х₀–;х₀) и (х₀;х₀+), причем на каждом из этих интервалов сохраняет знак. Тогда, если знаки на этих интервалах различны, то х₀ – точка перегиба; если одинаковы, то перегиба нет.

Доказательство. Если знаки на интервалах (х₀–;х₀) и (х₀;х₀+) различны, то на одном из отрезков [х₀–; х₀] и [х₀; х₀+] функция f(x) выпукла вверх, а на другом – вниз; это означает, что х₀ – точка перегиба. Если же знаки на интервалах (х₀–;х₀) и (х₀;х₀+) одинаковы, то на обоих отрезках [х₀–; х₀] и [х₀; х₀+] функция f(x) выпукла вверх или выпукла вниз; поэтому х₀ не является точкой перегиба. Теорема доказана.

Пример. Исследуем функцию f(x)=3х⁴–8х³+6х²–12 на монотонность и выпуклость.

1) =12х³–24х²+12х=12х(х²–2х+1)=12х(х–1)². Используем необходимое условие экстремума: поскольку существует при всех x, то точками экстремума могут быть только те точки, где =0, то есть точки x=0 и x=1. Составим таблицу:

	x<0	x=0	0<x<1	x=1	x>1
	–	0	+	0	+
f(x)	↘	min	↗		↗

Из таблицы видно, что в точке x=0 производная меняет знак с минуса на плюс, а в точке x=1 производная знак не меняет. Поэтому функция убывает на промежутке (–;0] и возрастает на промежутке [0;); x=0 – точка минимума.

2) =36х²–48х+12=12(3х–1)(х–1), существует при всех х. Точки перегиба надо искать среди точек, в которых =0, то есть среди точек х= и х=1. Составим таблицу:

	x<	x=	<x<1	x=1	x>1
	+	0	–	0	+
f(x)	⋃		⋂		⋃

Из таблицы видно, что >0 на промежутках

(–; ) и (1;) – здесь функция выпукла вниз; <0 на промежутке ( ;1) – здесь функция выпукла вверх. Точки х= и х=1 – точки перегиба. 