Уровни формализации при обеспечении процесса управления
Формальное описание процессов при управлении объектом в реальном времени тесно связано с моделированием, т.к. процесс замещения одной исследуемой системы понятиями и параметрами другой системы (моделирования) осуществляется как раз путем построения одного класса формул и отображения с помощью других, более простых формул и отображений.
Поэтому термины формальное описание и моделирование можно считать синонимами. Отображение одних объектов с помощью других требуется на всех уровнях представления объектов и процессов, начиная с концептуального уровня, поэтому к помощи моделей различного рода мы прибегаем всегда.
На уровне описания концепции используются самые простые модели, выполняющие скорее роль абстракции, без представления внутренних связей и функций и способных отобразить лишь основные цели и замыслы исследуемого объекта или процессы.
На функциональном уровне необходимы модели, умеющие показать связь между элементами и процессами в системе.
По мере детализации и уточнения процессов модели усложняются и становятся все более формализованными.
Отображением внешних функций и свойств моделируемой системы, с точки зрения функционирования, является статическая модель исследуемой системы.
Динамическую составляющую процесса моделирования обычно представляют либо в виде имитационного моделирования, либо в виде моделей с обратными связями.
Имитационное моделирование –
метод исследования, основанный на том, что изучаемая система заменяется ее имитатором, аналогом и с ним проводится эксперимент с целью получения информации об изучаемой системе.
По принципу исполнения модели делятся на:
формальные;
физические.
Формальные модели отображают изучаемый объект обычно в виде какой-либо абстракции:
формулы (математическая модель)
рисунка, схемы (графическая модель);
описания (логико-лингвистическая модель).
Физические модели более наглядны, более доступны для понимания и восприятия, поскольку их можно либо ощутить руками, либо увидеть глазами как уменьшенную и упрощенную материальную копию объекта или процесса.
Но физические модели часто нецелесообразны из-за своей высокой стоимости и уникальности (Иногда бывает просто невозможно выполнить).
Поэтому чаще всего применяют формальные модели, которые стали еще доступнее и дешевле, а главное более универсальны, потому что они реализуются на компьютерах.
Компьютер, благодаря программному принципу функционирования, дает самые широкие возможности как для описания любых формальных моделей процессов, так и для имитации поведения моделей.
Выделим следующие этапы проектирования модели и их реализации:
Постановка задачи моделирования – определение целей и задач исследования, определение структуры и свойств исследуемого объекта или процесса, принципов управления, оптимальных условий функционирования, методов обеспечения.
Сбор априорной информации – наиболее полное изучение объекта и процессов, выбор стратегии решения.
Выбор способа решения и реализации – определение типа модели, анализ модели по критериям адекватности и соответствия постоянным целям, определение структуры и параметров выходных величин с учетом выбранного критерия качества.
Проверка выбранного способа решения – предварительная оценка качества и адекватности модели, уточнения по структуре модели.
Реализация выбранного способа решения – исследования моделей методами имитационного моделирования и планирования эксперимента, уточнение целевых функций.
Анализ и интерпретация результатов – полный анализ полученных результатов, выводы о соответствии моделей, замечания, уточнения, рекомендации.
Рассмотрим сначала принципы построения моделей для организационных систем.
Здесь используется такой раздел математики как исследование операций.
Эта наука занимается разработкой и практическим применением методов оптимального управления организационными структурами и системами.
Здесь рассматриваются системы, которые состоят из большого числа взаимодействующих между собой подразделений, где интересы их не всегда согласуются между собой.
Математическая модель конструируется после выбора способа решения поставленной задачи.
В общем случае математическая модель решаемой задачи отображается следующим выражением:
Максимизировать 
При
ограничениях 
,
Где - целевая функция (т.е. показатель качества или эффективность системы);
– вектор управляемых переменных,
- вектор неуправляемых переменных,
– функция потребления i-го
ресурса,
– величина этого ресурса.
Для нахождения оптимального решения задачи в зависимости от вида целевой функции используются следующие методы:
Линейного программирования, если
- линейны относительно переменных;Нелинейные программирования, если - нелинейные относительно переменных
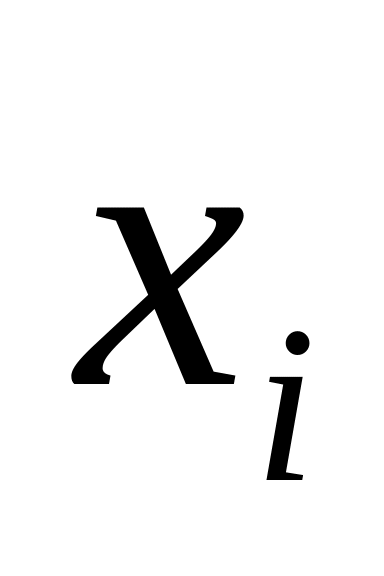.Динамическое программирование, если целевая функция
имеет специальную структуру, являясь
аддитивной
или мультипликативной
функцией от переменной
.
Функция
называется аддитивной,
если
и функция - мультипликативная,
если
Геометрическое программирование, если целевая функция
и
ограничения
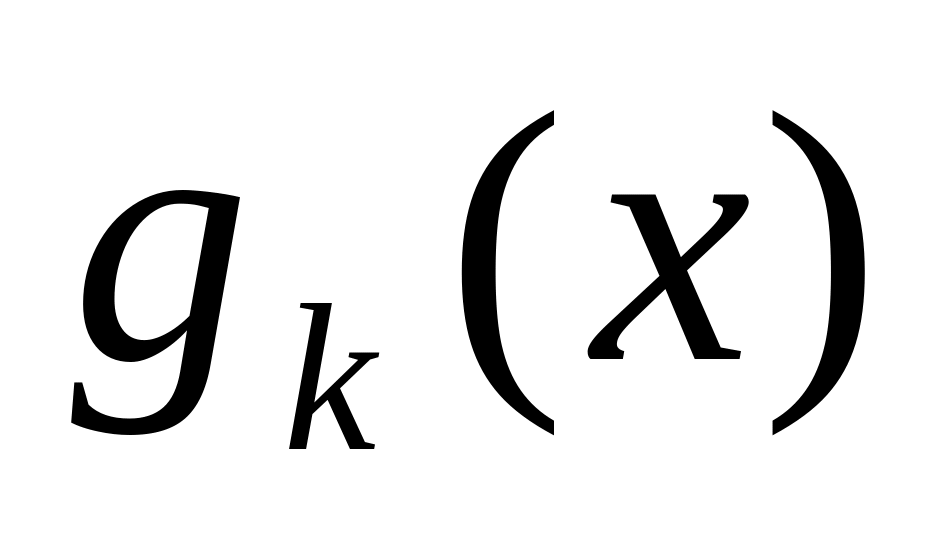представляют собой так называемые
функциональные номиналы.
Стохастическое программирование, когда вектор неуправляемых переменных случаен.
В этом случае надо максимизировать/минимизировать мат.ожидание при вероятностных ограничениях.
Дискретное программирование, если на переменные наложено условие дискретности, например, целочисленности.
Эвристическое программирование применяют тогда, когда найти точный оптимум в задаче обычным алгоритмическим путем не представляется возможным из-за огромного числа вариантов.
Тогда отказываются от поиска чисто оптимального решения и отыскивают с помощью специальных приемов, называемых эвристическими, удовлетворяющее данным условиям решение.
Эвристика – это процедура, правило, которое не основывается на формально доказанном алгоритме, а выводится на основании опыта, здравого смысла и интуиции.
Эвристики могут существенно сократить число возможных вариантов решения задачи и сделать эти решения предсказуемыми.
Из перечисленных выше методов наиболее распространенным и законченным является линейное программирование.
В сложных системах, к которым относятся системы организационного типа, модель лишь частично отображает реальный процесс. Поэтому необходима проверка степени соответствия или адекватности модели и реального процесса.
Проверку производят сравнение предсказанного поведения с фактическим при изменении значений внешних неуправляемых воздействий.
Корректировка решения может потребовать дополнительных исследований ОУ, уточнения структуры математической модели, многочисленных изменений переменных модели.
При этом в корректировке участвуют четыре компоненты:
вектор управляемых переменных;
вектор неуправляемых переменных;
выходные параметры объекта;
выходные параметры модели.
По своему содержанию задачи исследования операций можно разбить на следующие классы.
задачи управления запасами;
задачи распределения ресурсов;
задачи ремонта и замены оборудования (технического обслуживания);
задачи массового обслуживания;
задачи теории расписаний (календарного планирования);
задачи выбора маршрутов;
задачи сетевого планирования и управления;
задачи планировки и размещения;
комбинированные задачи.
Моделирование процессов управления объектом в реальном времени имеет свою специфику.
При этом модель должна отвечать на следующие вопросы:
обладает ли модель свойством живучести;
реализует ли она параллельные процессы;
обладает ли она способностью разрешать конфликтные ситуации;
имеет ли она механизмы для достижения поставленных задач.
Поэтому, более функционально полными являются модели процессов управления, которые способны ответить на сформулированные вопросы.
Такими моделями являются сети Петри.
[ Питерcон Дж. Теория сетей Перти и моделирование систем, 1984]