8. Проверка рабочего ослабления по элементам заданной схемы

1. Имеем фильтр со следующими элементами:

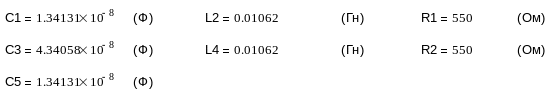
Получим с учетом нагрузочных сопротивлений формулы коэффициента передачи фильтра Т(р) и рабочего коэффициента передачи через денормированные величины элементов.

Р абочий коэффициент передачи для данного фильтра имеет вид:

где

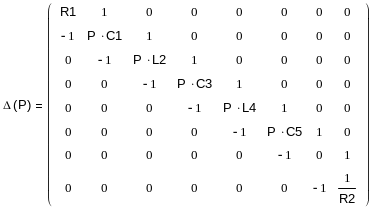
2.Расчитать А и В через полученный рабочий коэффициент передачи Т(р) при р = jω.

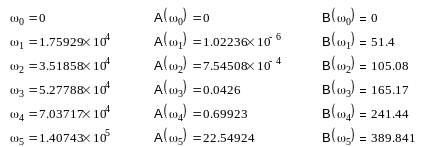
3. Рассчитать спектр последовательности прямоугольных импульсов на входе фильтра с параметрами: U_и = 1B, скважность N = T/ t_и = 5, следования импульсов f_и = 0.5 f₂.(рис.9).

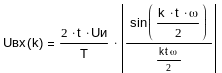
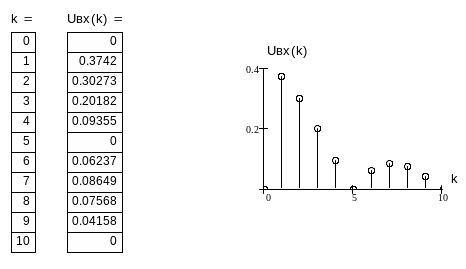
Рис.9 Спектр последовательности прямоугольных импульсов на входе фильтра

Спектр фаз (рис.10) найдем из выражения:

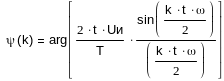
Рис.10 Спектр фаз

5.Расчитать спектр последовательности прямоугольных импульсов на выходе фильтра через полученный коэффициент передачи K(jω) (рис.11).

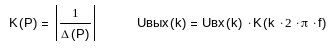
Рис.11 Спектр последовательности прямоугольных импульсов на выходе фильтра

6. Построить последовательность импульсов на выходе фильтра как сумму рассчитанных гармоник (рис.12).

где

Рис.12 Последовательность импульсов на выходе фильтра как сумма рассчитанных гармоник

7.Рассчитать переходную характеристику фильтра h(t) , используя полученный коэффициент передачи Т(р) (рис.13).

Операторное изображение Н(Р) переходной характеристики найдем по формуле:

Далее возьмем обратное преобразование Лапласа от полученного выражения. Окончательно получим:

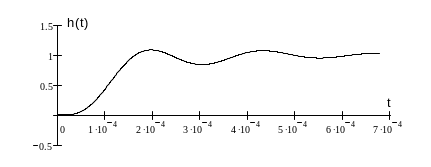
Рис.13 Переходная характеристика

8.Построить импульс на выходе фильтра, используя h(t) и h(t-t_i) (рис.14).

Импульс на выходе фильтра можно получить с помощью следующего выражения:

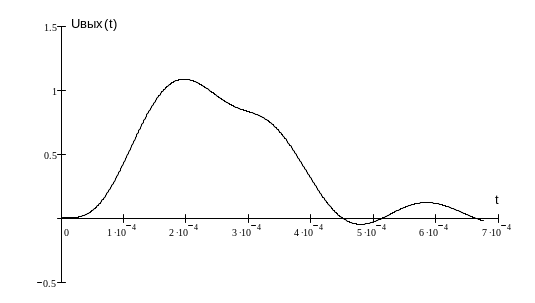
Рис.14 Импульс на выходе фильтра

Расчет показывает, что данные значения соответствуют ранее полученным результатам. Это свидетельствует о правильном выполнении этапов аппроксимации и реализации.

Список использованной литературы

1. Методическая разработка к курсовой работе по ТЭЦ “Расчет фильтров по рабочим параметрам”.

2. Бакалов В. П. Основы теории электрических цепей: Учебник для вузов. –М.: Радио и связь, 1986.

3. Белецкий А.Ф. Теория линейных электрических цепей: Учебник для вузов. – М.: Радио и связь, 1986.

4. Дьяконов В. Mathcad 8/2000: специальный справочник: “Питер”,2001.

18